Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 44017 by ajfour last updated on 20/Sep/18

Commented by ajfour last updated on 20/Sep/18

A cone is cut by a plane at an angle θ to its base and passes through a point at the base of cone. Find ratio of upper cone volume to lower cone volume. (in terms of θ, R, h ).

$${A}\:{cone}\:{is}\:{cut}\:{by}\:{a}\:{plane}\:\:{at}\:{an} \\ $$$${angle}\:\theta\:{to}\:{its}\:{base}\:{and}\:{passes} \\ $$$${through}\:{a}\:{point}\:{at}\:{the}\:{base}\:{of} \\ $$$${cone}.\:{Find}\:{ratio}\:{of}\:\boldsymbol{{upper}}\:\boldsymbol{{cone}} \\ $$$$\boldsymbol{{volume}}\:\boldsymbol{{to}}\:\boldsymbol{{lower}}\:\boldsymbol{{cone}}\:\boldsymbol{{volume}}. \\ $$$$\left({in}\:{terms}\:{of}\:\theta,\:{R},\:{h}\:\right). \\ $$

Commented by MrW3 last updated on 22/Sep/18

thank you sir!

$${thank}\:{you}\:{sir}!\: \\ $$

Commented by ajfour last updated on 22/Sep/18

heights of problem solving sir! haven′t comprehended it yet, however; you are Great sir, thanks for confirming again. let me try and understand, i will, coz you present it the best too.

$${heights}\:{of}\:{problem}\:{solving}\:{sir}! \\ $$$${haven}'{t}\:{comprehended}\:{it}\:{yet}, \\ $$$${however};\:{you}\:{are}\:\mathcal{G}{reat}\:{sir}, \\ $$$${thanks}\:{for}\:{confirming}\:{again}. \\ $$$${let}\:{me}\:{try}\:{and}\:{understand},\:{i}\:{will}, \\ $$$${coz}\:{you}\:{present}\:{it}\:{the}\:{best}\:{too}. \\ $$$$ \\ $$

Answered by MrW3 last updated on 24/Sep/18

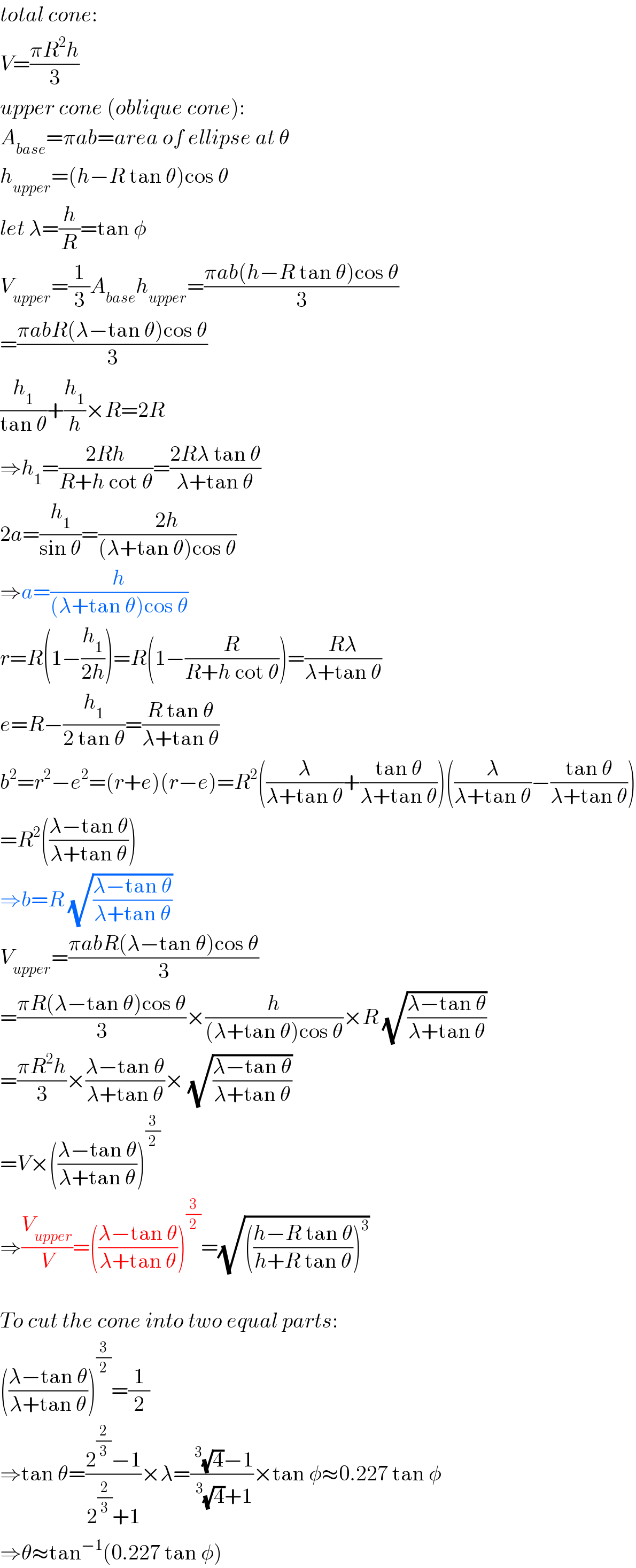
total cone: V=((πR^2 h)/3) upper cone (oblique cone): A_(base) =πab=area of ellipse at θ h_(upper) =(h−R tan θ)cos θ let λ=(h/R)=tan φ V_(upper) =(1/3)A_(base) h_(upper) =((πab(h−R tan θ)cos θ)/3) =((πabR(λ−tan θ)cos θ)/3) (h_1 /(tan θ))+(h_1 /h)×R=2R ⇒h_1 =((2Rh)/(R+h cot θ))=((2Rλ tan θ)/(λ+tan θ)) 2a=(h_1 /(sin θ))=((2h)/((λ+tan θ)cos θ)) ⇒a=(h/((λ+tan θ)cos θ)) r=R(1−(h_1 /(2h)))=R(1−(R/(R+h cot θ)))=((Rλ)/(λ+tan θ)) e=R−(h_1 /(2 tan θ))=((R tan θ)/(λ+tan θ)) b^2 =r^2 −e^2 =(r+e)(r−e)=R^2 ((λ/(λ+tan θ))+((tan θ)/(λ+tan θ)))((λ/(λ+tan θ))−((tan θ)/(λ+tan θ))) =R^2 (((λ−tan θ)/(λ+tan θ))) ⇒b=R (√((λ−tan θ)/(λ+tan θ))) V_(upper) =((πabR(λ−tan θ)cos θ)/3) =((πR(λ−tan θ)cos θ)/3)×(h/((λ+tan θ)cos θ))×R (√((λ−tan θ)/(λ+tan θ))) =((πR^2 h)/3)×((λ−tan θ)/(λ+tan θ))× (√((λ−tan θ)/(λ+tan θ))) =V×(((λ−tan θ)/(λ+tan θ)))^(3/2) ⇒(V_(upper) /V)=(((λ−tan θ)/(λ+tan θ)))^(3/2) =(√((((h−R tan θ)/(h+R tan θ)))^3 )) To cut the cone into two equal parts: (((λ−tan θ)/(λ+tan θ)))^(3/2) =(1/2) ⇒tan θ=((2^(2/3) −1)/(2^(2/3) +1))×λ=((^3 (√4)−1)/(^3 (√4)+1))×tan φ≈0.227 tan φ ⇒θ≈tan^(−1) (0.227 tan φ)

$${total}\:{cone}: \\ $$$${V}=\frac{\pi{R}^{\mathrm{2}} {h}}{\mathrm{3}} \\ $$$${upper}\:{cone}\:\left({oblique}\:{cone}\right): \\ $$$${A}_{{base}} =\pi{ab}={area}\:{of}\:{ellipse}\:{at}\:\theta \\ $$$${h}_{{upper}} =\left({h}−{R}\:\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta \\ $$$${let}\:\lambda=\frac{{h}}{{R}}=\mathrm{tan}\:\phi \\ $$$${V}_{{upper}} =\frac{\mathrm{1}}{\mathrm{3}}{A}_{{base}} {h}_{{upper}} =\frac{\pi{ab}\left({h}−{R}\:\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta}{\mathrm{3}} \\ $$$$=\frac{\pi{abR}\left(\lambda−\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta}{\mathrm{3}} \\ $$$$\frac{{h}_{\mathrm{1}} }{\mathrm{tan}\:\theta}+\frac{{h}_{\mathrm{1}} }{{h}}×{R}=\mathrm{2}{R} \\ $$$$\Rightarrow{h}_{\mathrm{1}} =\frac{\mathrm{2}{Rh}}{{R}+{h}\:\mathrm{cot}\:\theta}=\frac{\mathrm{2}{R}\lambda\:\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta} \\ $$$$\mathrm{2}{a}=\frac{{h}_{\mathrm{1}} }{\mathrm{sin}\:\theta}=\frac{\mathrm{2}{h}}{\left(\lambda+\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta} \\ $$$$\Rightarrow{a}=\frac{{h}}{\left(\lambda+\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta} \\ $$$${r}={R}\left(\mathrm{1}−\frac{{h}_{\mathrm{1}} }{\mathrm{2}{h}}\right)={R}\left(\mathrm{1}−\frac{{R}}{{R}+{h}\:\mathrm{cot}\:\theta}\right)=\frac{{R}\lambda}{\lambda+\mathrm{tan}\:\theta} \\ $$$${e}={R}−\frac{{h}_{\mathrm{1}} }{\mathrm{2}\:\mathrm{tan}\:\theta}=\frac{{R}\:\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta} \\ $$$${b}^{\mathrm{2}} ={r}^{\mathrm{2}} −{e}^{\mathrm{2}} =\left({r}+{e}\right)\left({r}−{e}\right)={R}^{\mathrm{2}} \left(\frac{\lambda}{\lambda+\mathrm{tan}\:\theta}+\frac{\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}\right)\left(\frac{\lambda}{\lambda+\mathrm{tan}\:\theta}−\frac{\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}\right) \\ $$$$={R}^{\mathrm{2}} \left(\frac{\lambda−\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}\right) \\ $$$$\Rightarrow{b}={R}\:\sqrt{\frac{\lambda−\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}} \\ $$$${V}_{{upper}} =\frac{\pi{abR}\left(\lambda−\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta}{\mathrm{3}} \\ $$$$=\frac{\pi{R}\left(\lambda−\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta}{\mathrm{3}}×\frac{{h}}{\left(\lambda+\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta}×{R}\:\sqrt{\frac{\lambda−\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}} \\ $$$$=\frac{\pi{R}^{\mathrm{2}} {h}}{\mathrm{3}}×\frac{\lambda−\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}×\:\sqrt{\frac{\lambda−\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}} \\ $$$$={V}×\left(\frac{\lambda−\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\Rightarrow\frac{{V}_{{upper}} }{{V}}=\left(\frac{\lambda−\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\sqrt{\left(\frac{{h}−{R}\:\mathrm{tan}\:\theta}{{h}+{R}\:\mathrm{tan}\:\theta}\right)^{\mathrm{3}} } \\ $$$$ \\ $$$${To}\:{cut}\:{the}\:{cone}\:{into}\:{two}\:{equal}\:{parts}: \\ $$$$\left(\frac{\lambda−\mathrm{tan}\:\theta}{\lambda+\mathrm{tan}\:\theta}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{1}}×\lambda=\frac{\:^{\mathrm{3}} \sqrt{\mathrm{4}}−\mathrm{1}}{\:^{\mathrm{3}} \sqrt{\mathrm{4}}+\mathrm{1}}×\mathrm{tan}\:\phi\approx\mathrm{0}.\mathrm{227}\:\mathrm{tan}\:\phi \\ $$$$\Rightarrow\theta\approx\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{227}\:\mathrm{tan}\:\phi\right) \\ $$

Commented by MrW3 last updated on 22/Sep/18

Commented by MrW3 last updated on 22/Sep/18

Commented by ajfour last updated on 17/Nov/18

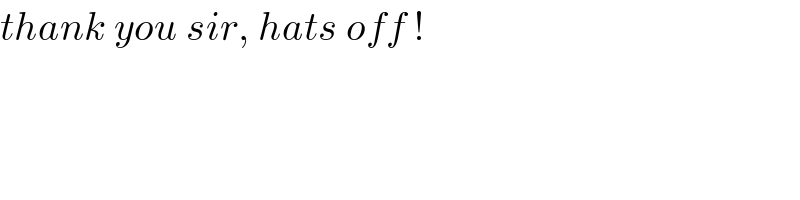
thank you sir, hats off !

$${thank}\:{you}\:{sir},\:{hats}\:{off}\:!\: \\ $$

Commented by MrW3 last updated on 23/Sep/18

Commented by ajfour last updated on 17/Nov/18

Sir,i have difficulty in under- standing b^2 +e^2 = r^2 ; but you have already explained,let me try again, thanks.

$${Sir},{i}\:{have}\:{difficulty}\:{in}\:{under}- \\ $$$${standing}\:\:{b}^{\mathrm{2}} +{e}^{\mathrm{2}} =\:{r}^{\mathrm{2}} \:;\:{but}\:{you} \\ $$$${have}\:{already}\:{explained},{let}\:{me} \\ $$$${try}\:{again},\:{thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com