Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 44159 by rahul 19 last updated on 22/Sep/18

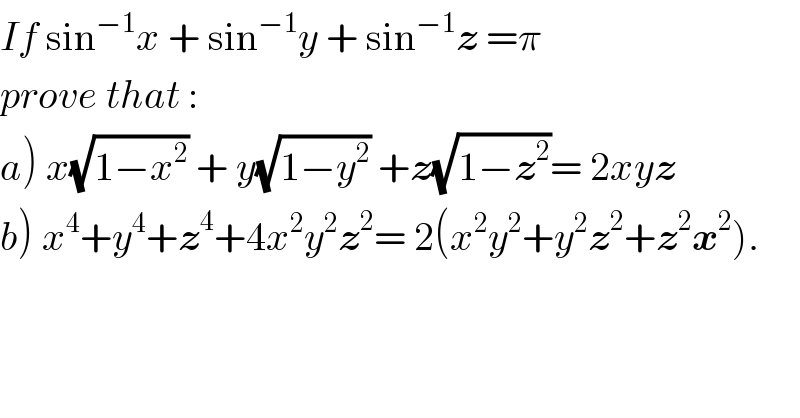
If sin^(−1) x + sin^(−1) y + sin^(−1) z =π prove that : a) x(√(1−x^2 )) + y(√(1−y^2 )) +z(√(1−z^2 ))= 2xyz b) x^4 +y^4 +z^4 +4x^2 y^2 z^2 = 2(x^2 y^2 +y^2 z^2 +z^2 x^2 ).

$${If}\:\mathrm{sin}^{−\mathrm{1}} {x}\:+\:\mathrm{sin}^{−\mathrm{1}} {y}\:+\:\mathrm{sin}^{−\mathrm{1}} \boldsymbol{{z}}\:=\pi\: \\ $$$${prove}\:{that}\:: \\ $$$$\left.{a}\right)\:{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\:{y}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:+\boldsymbol{{z}}\sqrt{\mathrm{1}−\boldsymbol{{z}}^{\mathrm{2}} }=\:\mathrm{2}{xy}\boldsymbol{{z}} \\ $$$$\left.{b}\right)\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +\boldsymbol{{z}}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \boldsymbol{{z}}^{\mathrm{2}} =\:\mathrm{2}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} \boldsymbol{{z}}^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} \boldsymbol{{x}}^{\mathrm{2}} \right). \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 22/Sep/18

sinα=x sinβ=y sinγ=z α+β+γ=Π a)LHS sinαcosα+sinβcosβ+sinγcosγ (1/2)(sin2α+sin2β+sin2γ) (1/2){2sin(α+β)cos(α−β)+2sinγcosγ} sin(Π−γ)cos(α−β)+sinγcosγ sinγ{cos(α−β)+cosγ} sinγ{2cos(((α+γ−β)/2))cos(((α−β−γ)/2))} 2sinγ{cos((Π/2)−β)cos(((α−(Π−α))/2)} 2sinγsinβcos{−((Π/2)−α)} cos(−θ)=cosθ so 2sinγ.sinβ.sinα=2xyz proved

$${sin}\alpha={x}\:\:\:{sin}\beta={y}\:\:\:\:{sin}\gamma={z} \\ $$$$\alpha+\beta+\gamma=\Pi \\ $$$$\left.{a}\right){LHS} \\ $$$${sin}\alpha{cos}\alpha+{sin}\beta{cos}\beta+{sin}\gamma{cos}\gamma \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({sin}\mathrm{2}\alpha+{sin}\mathrm{2}\beta+{sin}\mathrm{2}\gamma\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2}{sin}\left(\alpha+\beta\right){cos}\left(\alpha−\beta\right)+\mathrm{2}{sin}\gamma{cos}\gamma\right\} \\ $$$${sin}\left(\Pi−\gamma\right){cos}\left(\alpha−\beta\right)+{sin}\gamma{cos}\gamma \\ $$$${sin}\gamma\left\{{cos}\left(\alpha−\beta\right)+{cos}\gamma\right\} \\ $$$${sin}\gamma\left\{\mathrm{2}{cos}\left(\frac{\alpha+\gamma−\beta}{\mathrm{2}}\right){cos}\left(\frac{\alpha−\beta−\gamma}{\mathrm{2}}\right)\right\} \\ $$$$\mathrm{2}{sin}\gamma\left\{{cos}\left(\frac{\Pi}{\mathrm{2}}−\beta\right){cos}\left(\frac{\alpha−\left(\Pi−\alpha\right)}{\mathrm{2}}\right\}\right. \\ $$$$\mathrm{2}{sin}\gamma{sin}\beta{cos}\left\{−\left(\frac{\Pi}{\mathrm{2}}−\alpha\right)\right\} \\ $$$${cos}\left(−\theta\right)={cos}\theta \\ $$$${so}\:\mathrm{2}{sin}\gamma.{sin}\beta.{sin}\alpha=\mathrm{2}{xyz}\:\:\:{proved} \\ $$

Commented by rahul 19 last updated on 22/Sep/18

thanks sir ����

Commented by peter frank last updated on 23/Sep/18

big up

$${big}\:{up} \\ $$

Answered by math1967 last updated on 22/Sep/18

a) let sin^(−1) x=A,sin^(−1) y=B,sin^(−1) z=C ∴sinA=x ,sinB=y ,sinC=z also A+B+C=π L.H.S x(√(1−x^2 )) +y(√(1−y^2 )) +z(√(1−z^2 )) =SinAcosA+sinBcosB+sinCcosC =(1/2)(sin2A+sin2B)+sinCcosC =(1/2)×2sin(A+B)cos(A−B)+sinCcosC =sinCcos(A−B)+sinCcosC [∵A+B=π−C] =sinC{cos(A−B)+cos(π−A−B)} =2sinCsinAsinB =2xyz=R.H.S prove

$$\left.{a}\right)\:{let}\:\mathrm{sin}^{−\mathrm{1}} {x}={A},\mathrm{sin}^{−\mathrm{1}} {y}={B},\mathrm{sin}^{−\mathrm{1}} {z}={C} \\ $$$$\therefore{sinA}={x}\:,{sinB}={y}\:,{sinC}={z} \\ $$$${also}\:{A}+{B}+{C}=\pi \\ $$$${L}.{H}.{S}\:{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+{y}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:+{z}\sqrt{\mathrm{1}−{z}^{\mathrm{2}} } \\ $$$$={SinAcosA}+{sinBcosB}+{sinCcosC} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({sin}\mathrm{2}{A}+{sin}\mathrm{2}{B}\right)+{sinCcosC} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}{sin}\left({A}+{B}\right){cos}\left({A}−{B}\right)+{sinCcosC} \\ $$$$={sinCcos}\left({A}−{B}\right)+{sinCcosC} \\ $$$$\left[\because{A}+{B}=\pi−{C}\right] \\ $$$$={sinC}\left\{{cos}\left({A}−{B}\right)+{cos}\left(\pi−{A}−{B}\right)\right\} \\ $$$$=\mathrm{2}{sinCsinAsinB} \\ $$$$=\mathrm{2}{xyz}={R}.{H}.{S}\:{prove} \\ $$

Answered by math1967 last updated on 22/Sep/18

b)sin^(−1) x+sin^(−1) y=π−sin^(−1) z sin^(−1) (x(√(1−y^2 )) +y(√(1−x^2 ))=π−sin^(−1) z (x(√(1−y^2 )) +y(√(1−x^2 ))=sin(π−sin^(−1) z) x(√(1−y^2 )) +y(√(1−x^2 ))=z (x(√(1−y^2 )) )^2 =z^2 +y^2 −x^2 y^2 −2zy(√(1−x^2 )) (x^2 −y^2 −z^2 )^ =(−2zy(√(1−x^2 )) )^2 x^4 +y^4 +z^4 −2x^2 y^2 −2z^2 x^2 +2y^2 z^2 =4z^2 y^2 −4x^2 y^2 z^2 ∴x^4 +y^4 +z^4 +4x^2 y^2 z^2 =2(x^2 y^2 +y^2 z^2 +z^2 x^2 ) Proved

$$\left.{b}\right)\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} {y}=\pi−\mathrm{sin}^{−\mathrm{1}} {z} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left({x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:+{y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\pi−\mathrm{sin}^{−\mathrm{1}} {z}\right. \\ $$$$\left({x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:+{y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }={sin}\left(\pi−\mathrm{sin}^{−\mathrm{1}} {z}\right)\right. \\ $$$${x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:+{y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }={z} \\ $$$$\left({x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:\right)^{\mathrm{2}} ={z}^{\mathrm{2}} +{y}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} \:−\mathrm{2}{zy}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{z}^{\mathrm{2}} \right)^{} =\left(−\mathrm{2}{zy}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{2}{z}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} {z}^{\mathrm{2}} =\mathrm{4}{z}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} \\ $$$$\therefore{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} =\mathrm{2}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} \right) \\ $$$${Proved} \\ $$

Commented by rahul 19 last updated on 22/Sep/18

thanks sir ����

Terms of Service

Privacy Policy

Contact: info@tinkutara.com