Question and Answers Forum
Question Number 44201 by abdo.msup.com last updated on 23/Sep/18
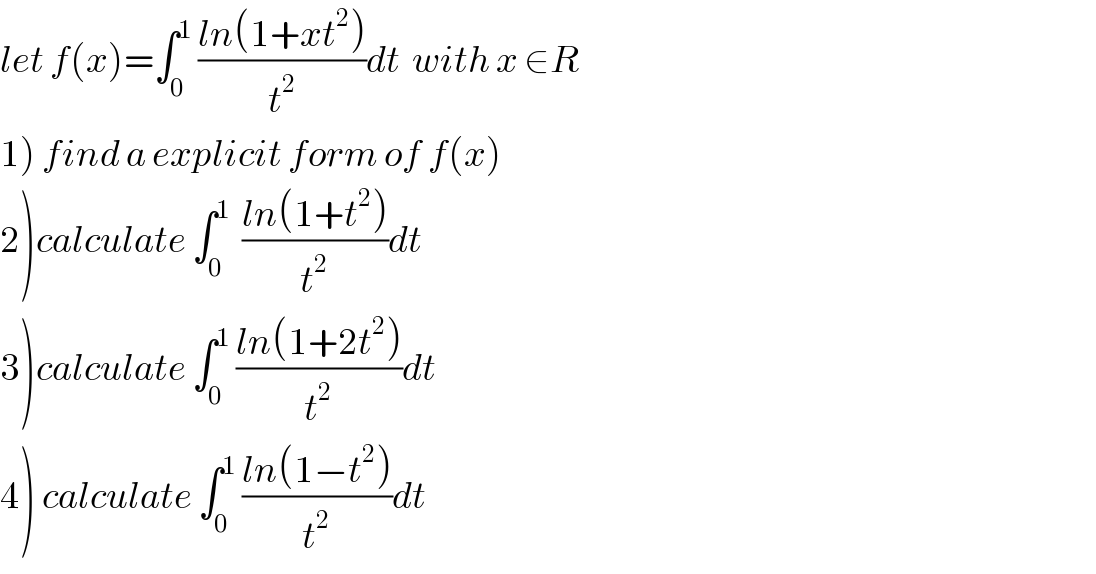
Commented by maxmathsup by imad last updated on 25/Sep/18
![1) we have f^′ (x) = ∫_0 ^1 (t^2 /(t^2 (1+xt^2 )))dt = ∫_0 ^1 (dt/(1 +xt^2 )) case 1 x>0 changement t(√x)=u give f^′ (x)= ∫_0 ^(√x) (1/(1+u^2 )) (du/(√x)) =(1/(√x)) arctan((√x)) ⇒ f(x) =∫_0 ^x ((arctan((√t)))/(√t)) dt +c but c=f(0)=0 ⇒ f(x) =∫_0 ^x ((actan((√t)))/(√t))dt =_((√t)=u) ∫_0 ^(√x) ((arctan(u))/u) (2u)du =2 ∫_0 ^(√x) arctanu du by parts f(x) =2{ [u arctanu]_0 ^(√x) −∫_0 ^(√x) (u/(1+u^2 ))du} =2{(√x)arctan((√x)) −[(1/2)ln(1+u^2 )]_0 ^(√x) } =2{ (√x)arctan((√x)) −(1/2)ln(1+x)} ⇒f(x)=2(√x)arctan((√x))−ln(1+x) case 2 x<0 ⇒f^′ (x)= ∫_0 ^1 (dt/(1−(−x)t^2 )) =_(t(√(−x))=u) ∫_0 ^(√(−x)) (1/(1−u^2 )) (du/(√(−x))) =(1/(2(√(−x)))){ ∫_0 ^(√(−x)) { (1/(1−u)) +(1/(1+u))}du} = (1/(2(√(−x))))[ln∣((1+u)/(1−u))∣]_0 ^(√(−x)) ⇒ f^′ (x) = (1/(2(√(−x))))ln∣((1+(√(−x)))/(1−(√(−x))))∣ ⇒f(x) = ∫_x ^0 (1/(2(√(−t))))ln∣((1+(√(−t)))/(1−(√(−t))))∣ +c c=f(0) =0 ⇒f(x)= ∫_x ^0 (1/(2(√(−t))))ln∣((1+(√(−t)))/(1−(√(−t))))∣ dt changement (√(−t))=u give f(x) = ∫_(√(−x)) ^0 (1/(2u))ln∣((1+u)/(1−u))∣(−2u)du = ∫_0 ^(√(−x)) ln∣1+u∣du−∫_0 ^(√(−x)) ln∣1−u∣ du =∫_0 ^(√(−x)) ln(1+u)du −∫_0 ^(√(−x)) ln(1−u)du but ∫_0 ^(√(−x)) ln(1+u)du =_(1+u =α) ∫_1 ^(1+(√(−x))) ln(α)dα [αln(α)−α]_1 ^(1+(√(−x))) =(1+(√(−x)))ln(1+(√(−x)))−(1+(√(−x))) +1 =(1+(√(−x)))ln(1+(√(−x))) −(√(−x)).also ∫_0 ^(√(−x)) ln(1−u)du =_(1−u =α) −∫_1 ^(1−(√(−x))) ln(α)dα =−[αln(α) −α]_1 ^(1−(√(−x))) =−{(1−(√(−x)))ln(1−(√(−x)))−(1−(√(−x))) +1} =−(1−(√(−x)))ln(1−(√(−x))) −(√(−x)) ⇒ f(x)=(1+(√(−x)))ln(1+(√(−x))) +(1−(√(−x)))ln(1−(√(−x))).](Q44285.png)
Commented by maxmathsup by imad last updated on 25/Sep/18
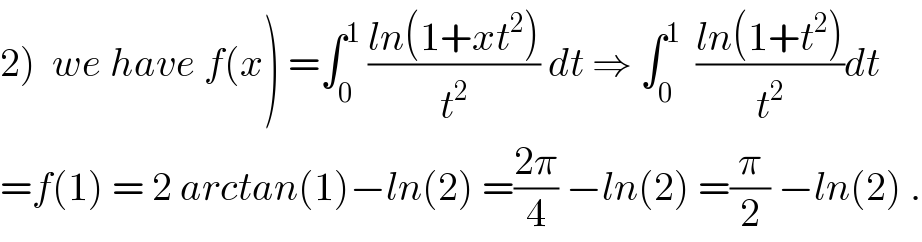
Commented by maxmathsup by imad last updated on 25/Sep/18
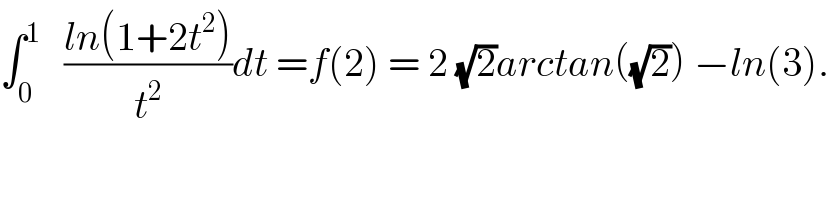
Commented by maxmathsup by imad last updated on 25/Sep/18
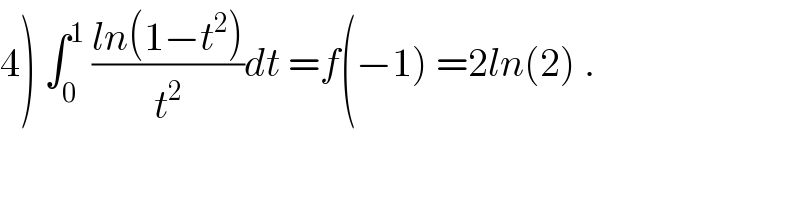
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Sep/18