
Question and Answers Forum
Question Number 44230 by behi83417@gmail.com last updated on 24/Sep/18

Answered by MrW3 last updated on 25/Sep/18
![(1) f(x,y)=x^2 +xy+y^2 −ax−by (∂f/∂x)=2x+y−a=0 ...(i) (∂f/∂y)=x+2y−b=0 ...(ii) 3x−2a+b=0 x=((2a−b)/3) 3y−2b+a=0 y=((2b−a)/3) f_(min) =(((2a−b)/3))^2 +(((2a−b)/3))(((2b−a)/3))+(((2b−a)/3))^2 −a(((2a−b)/3))−b(((2b−a)/3)) =(1/9)[4a^2 −4ab+b^2 +4ab−2b^2 −2a^2 +ab+4b^2 −4ab+a^2 −6a^2 +3ab−6b^2 +3ab] =(1/3)(ab−a^2 −b^2 ) (2) g(x,y)=(((ax+by+c)^2 )/(x^2 +y^2 +1)) (∂g/∂x)=−((2x(ax+by+c)^2 )/((x^2 +y^2 +1)^2 ))+((2a(ax+by+c))/(x^2 +y^2 +1))=0 x(ax+by+c)=a(x^2 +y^2 +1) ...(i) (∂g/∂y)=−((2y(ax+by+c)^2 )/((x^2 +y^2 +1)^2 ))+((2b(ax+by+c))/(x^2 +y^2 +1))=0 y(ax+by+c)=b(x^2 +y^2 +1) ...(ii) (x/a)=(y/b) x(ax+((b^2 x)/a)+c)=a(x^2 +((b^2 x^2 )/a^2 )+1) ax(a^2 x+b^2 x+ac)=a(a^2 x^2 +b^2 x^2 +a^2 ) ⇒x=(a/c) ⇒y=(b/c) ⇒g_(max) =((((a^2 /c)+(b^2 /c)+c)^2 )/((a^2 /c^2 )+(b^2 /c^2 )+1))=a^2 +b^2 +c^2](Q44256.png)
Commented by behi83417@gmail.com last updated on 25/Sep/18

Commented by tanmay.chaudhury50@gmail.com last updated on 25/Sep/18
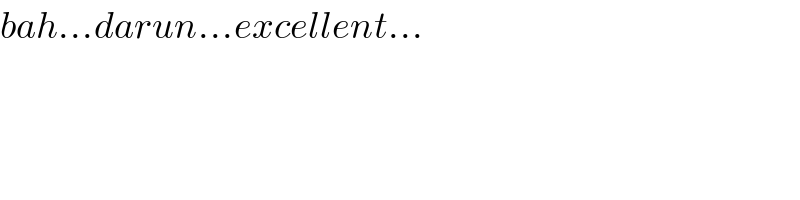
Commented by MrW3 last updated on 25/Sep/18
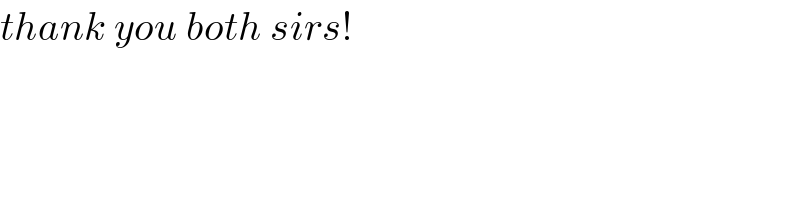
Commented by rahul 19 last updated on 26/Sep/18
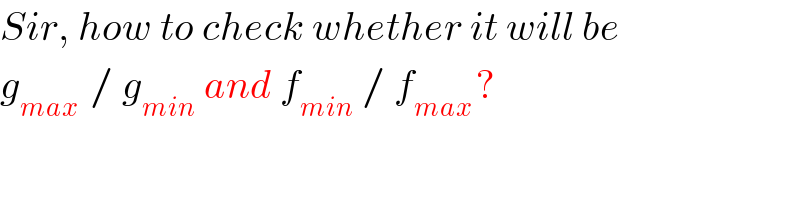
Commented by MrW3 last updated on 26/Sep/18
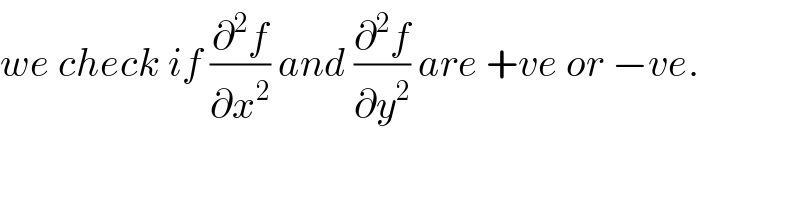
Commented by rahul 19 last updated on 26/Sep/18
Commented by MrW3 last updated on 26/Sep/18

Commented by rahul 19 last updated on 26/Sep/18

