
Question Number 4441 by Rasheed Soomro last updated on 27/Jan/16
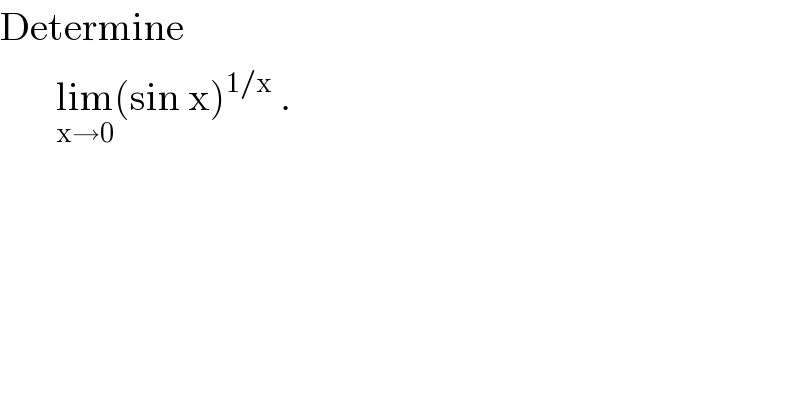
$$\mathrm{Determine}\: \\ $$$$\:\:\:\:\:\:\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{1}/\mathrm{x}} \:. \\ $$
Commented by Yozzii last updated on 29/Jan/16
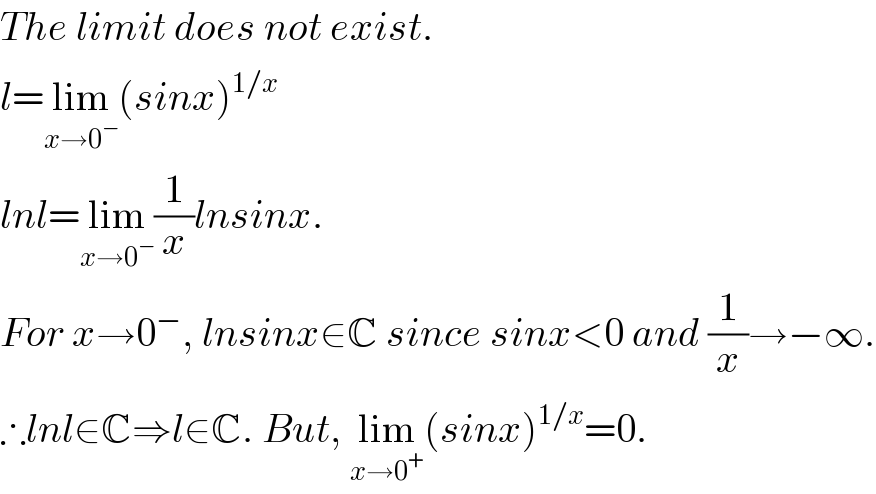
$${The}\:{limit}\:{does}\:{not}\:{exist}. \\ $$$${l}=\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\left({sinx}\right)^{\mathrm{1}/{x}} \\ $$$${lnl}=\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{\mathrm{1}}{{x}}{lnsinx}. \\ $$$${For}\:{x}\rightarrow\mathrm{0}^{−} ,\:{lnsinx}\in\mathbb{C}\:{since}\:{sinx}<\mathrm{0}\:{and}\:\frac{\mathrm{1}}{{x}}\rightarrow−\infty. \\ $$$$\therefore{lnl}\in\mathbb{C}\Rightarrow{l}\in\mathbb{C}.\:{But},\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left({sinx}\right)^{\mathrm{1}/{x}} =\mathrm{0}. \\ $$
Commented by Jens last updated on 29/Jan/16

$${Put}\:{y}\:=\mathrm{1}/{x}.\:{Then}\:{sinx}={sin}\left(\mathrm{1}/{y}\right) \\ $$$$\Rightarrow\mathrm{1}/{y}\:{as}\:{y}\Rightarrow\infty\:{so}\:\left({sinx}\right)^{\mathrm{1}/{x}} \Rightarrow \\ $$$$\left(\mathrm{1}/{y}\right)^{{y}} =\mathrm{1}/{y}^{{y}} \Rightarrow\mathrm{0}\:{for}\:{y}\:\Rightarrow\infty\:{so}\:{the} \\ $$$${limit}\:{does}\:{exist}! \\ $$
Commented by Yozzii last updated on 30/Jan/16
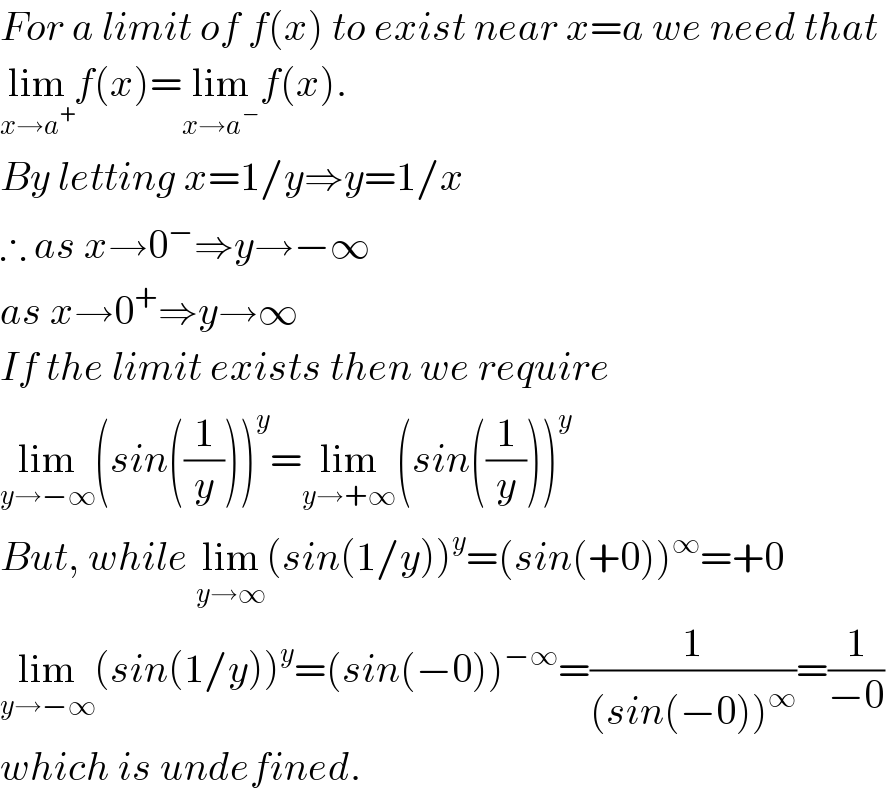
$${For}\:{a}\:{limit}\:{of}\:{f}\left({x}\right)\:{to}\:{exist}\:{near}\:{x}={a}\:{we}\:{need}\:{that}\: \\ $$$$\underset{{x}\rightarrow{a}^{+} } {\mathrm{lim}}{f}\left({x}\right)=\underset{{x}\rightarrow{a}^{−} } {\mathrm{lim}}{f}\left({x}\right). \\ $$$${By}\:{letting}\:{x}=\mathrm{1}/{y}\Rightarrow{y}=\mathrm{1}/{x} \\ $$$$\therefore\:{as}\:{x}\rightarrow\mathrm{0}^{−} \Rightarrow{y}\rightarrow−\infty \\ $$$${as}\:{x}\rightarrow\mathrm{0}^{+} \Rightarrow{y}\rightarrow\infty \\ $$$${If}\:{the}\:{limit}\:{exists}\:{then}\:{we}\:{require} \\ $$$$\underset{{y}\rightarrow−\infty} {\mathrm{lim}}\left({sin}\left(\frac{\mathrm{1}}{{y}}\right)\right)^{{y}} =\underset{{y}\rightarrow+\infty} {\mathrm{lim}}\left({sin}\left(\frac{\mathrm{1}}{{y}}\right)\right)^{{y}} \\ $$$${But},\:{while}\:\underset{{y}\rightarrow\infty} {\mathrm{lim}}\left({sin}\left(\mathrm{1}/{y}\right)\right)^{{y}} =\left({sin}\left(+\mathrm{0}\right)\right)^{\infty} =+\mathrm{0}\: \\ $$$$\underset{{y}\rightarrow−\infty} {\mathrm{lim}}\left({sin}\left(\mathrm{1}/{y}\right)\right)^{{y}} =\left({sin}\left(−\mathrm{0}\right)\right)^{−\infty} =\frac{\mathrm{1}}{\left({sin}\left(−\mathrm{0}\right)\right)^{\infty} }=\frac{\mathrm{1}}{−\mathrm{0}}\: \\ $$$${which}\:{is}\:{undefined}. \\ $$
Commented by Yozzii last updated on 30/Jan/16

Commented by Yozzii last updated on 30/Jan/16

$${For}\:{negative}\:{x}\:{near}\:{zero},\: \\ $$$${no}\:{real}\:{value}\:{of}\:\left({sinx}\right)^{\mathrm{1}/{x}} \:{exists}. \\ $$$$ \\ $$
