Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 44476 by abdo.msup.com last updated on 29/Sep/18

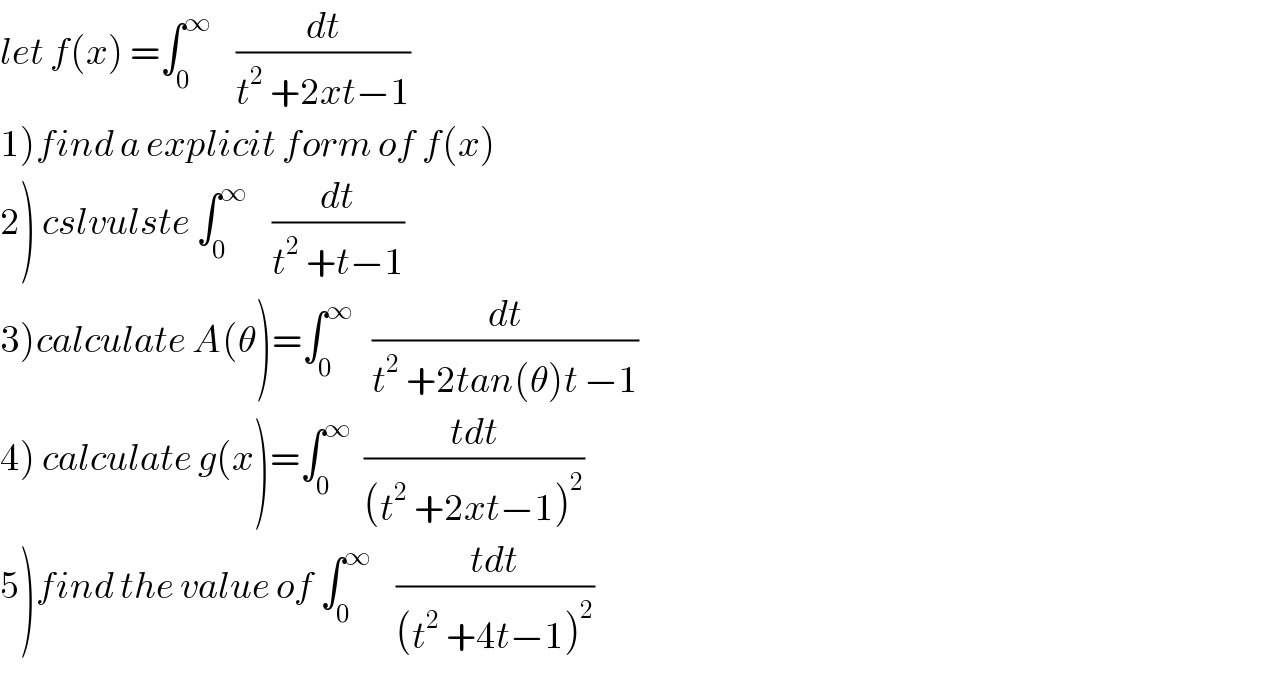
let f(x) =∫_0 ^∞ (dt/(t^2 +2xt−1)) 1)find a explicit form of f(x) 2) cslvulste ∫_0 ^∞ (dt/(t^2 +t−1)) 3)calculate A(θ)=∫_0 ^∞ (dt/(t^2 +2tan(θ)t −1)) 4) calculate g(x)=∫_0 ^∞ ((tdt)/((t^2 +2xt−1)^2 )) 5)find the value of ∫_0 ^∞ ((tdt)/((t^2 +4t−1)^2 ))

$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{2}{xt}−\mathrm{1}} \\ $$$$\left.\mathrm{1}\right){find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{cslvulste}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}−\mathrm{1}} \\ $$$$\left.\mathrm{3}\right){calculate}\:{A}\left(\theta\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{2}{tan}\left(\theta\right){t}\:−\mathrm{1}} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:{g}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{tdt}}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{xt}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{5}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{tdt}}{\left({t}^{\mathrm{2}} \:+\mathrm{4}{t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Commented by maxmathsup by imad last updated on 01/Oct/18

1) we have f(x) =∫_0 ^∞ (dt/(t^2 +2xt+x^2 −x^2 −1)) = ∫_0 ^∞ (dt/((t+x)^2 −(x^2 +1))) =∫_0 ^∞ (dt/((t+x+(√(1+x^2 )))(t+x−(√(1+x^2 ))))) =(1/(2(√(1+x^2 )))) ∫_0 ^∞ ((1/(t+x−(√(1+x^2 )))) −(1/(t+x +(√(1+x^2 )))))dt =(1/(2(√(1+x^2 ))))[ln∣((t+x−(√(1+x^2 )))/(t+x+(√(1+x^2 ))))]_0 ^(+∞) =(1/(2(√(1+x^2 ))))(−ln∣((x−(√(1+x^2 )))/(x+(√(1+x^2 ))))∣) ⇒f(x)=(1/(2(√(1+x^2 ))))ln∣((x+(√(1+x^2 )))/(x−(√(1+x^2 ))))∣ .

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{2}{xt}+{x}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dt}}{\left({t}+{x}\right)^{\mathrm{2}} −\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{\left({t}+{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\left({t}+{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\left(\frac{\mathrm{1}}{{t}+{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:−\frac{\mathrm{1}}{{t}+{x}\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\left[{ln}\mid\frac{{t}+{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{t}+{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\left(−{ln}\mid\frac{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\mid\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{ln}\mid\frac{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\mid\:. \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 01/Oct/18

2) ∫_0 ^∞ (dt/(t^2 +t −1)) =f((1/2)) = (1/(2(√(1+(1/4)))))ln∣(((1/2)+(√(1+(1/4))))/((1/2)−(√(1+(1/4)))))∣ =(1/(√5))ln(((1+(√5))/((√5)−1))) .

$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}\:−\mathrm{1}}\:={f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}}}{ln}\mid\frac{\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}}}{\frac{\mathrm{1}}{\mathrm{2}}−\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}}}\mid \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{5}}−\mathrm{1}}\right)\:. \\ $$

Commented by maxmathsup by imad last updated on 01/Oct/18

3) we have ∫_0 ^∞ (dt/(t^2 −2tanθ t −1)) =f(tanθ) = (1/(2(√(1+tan^2 θ))))ln∣((tanθ +(√(1+tan^2 θ)))/(tanθ −(√(1+tan^2 θ))))∣ =((∣cosθ∣)/2)ln∣ ((tanθ +(1/(∣cosθ∣)))/(tanθ−(1/(∣cosθ∣))))∣ =((∣cosθ∣)/2)ln∣((ξ(θ)sinθ +1)/(ξ(θ)−1)) ∣ with ξ(θ)=((cosθ)/(∣cosθ∣)) =+^− 1

$$\left.\mathrm{3}\right)\:{we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}{tan}\theta\:{t}\:−\mathrm{1}}\:={f}\left({tan}\theta\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}{ln}\mid\frac{{tan}\theta\:+\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}{{tan}\theta\:−\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}\mid \\ $$$$=\frac{\mid{cos}\theta\mid}{\mathrm{2}}{ln}\mid\:\frac{{tan}\theta\:+\frac{\mathrm{1}}{\mid{cos}\theta\mid}}{{tan}\theta−\frac{\mathrm{1}}{\mid{cos}\theta\mid}}\mid\:=\frac{\mid{cos}\theta\mid}{\mathrm{2}}{ln}\mid\frac{\xi\left(\theta\right){sin}\theta\:+\mathrm{1}}{\xi\left(\theta\right)−\mathrm{1}}\:\mid\:{with}\:\xi\left(\theta\right)=\frac{{cos}\theta}{\mid{cos}\theta\mid}\:=\overset{−} {+}\mathrm{1} \\ $$

Commented by maxmathsup by imad last updated on 01/Oct/18

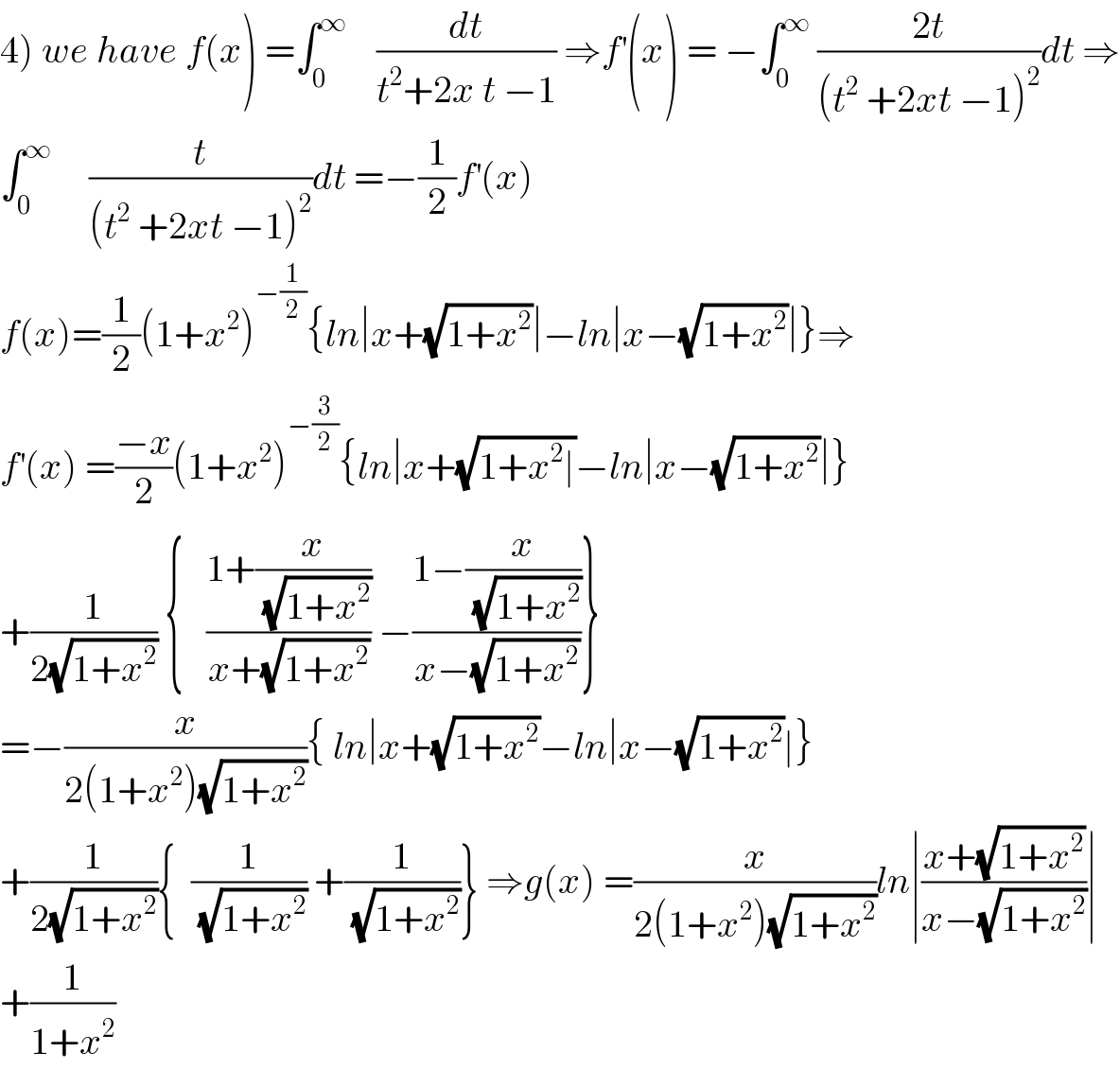
4) we have f(x) =∫_0 ^∞ (dt/(t^2 +2x t −1)) ⇒f^′ (x) = −∫_0 ^∞ ((2t)/((t^2 +2xt −1)^2 ))dt ⇒ ∫_0 ^∞ (t/((t^2 +2xt −1)^2 ))dt =−(1/2)f^′ (x) f(x)=(1/2)(1+x^2 )^(−(1/2)) {ln∣x+(√(1+x^2 ))∣−ln∣x−(√(1+x^2 ))∣}⇒ f^′ (x) =((−x)/2)(1+x^2 )^(−(3/2)) {ln∣x+(√(1+x^2 ∣))−ln∣x−(√(1+x^2 ))∣} +(1/(2(√(1+x^2 )))) { ((1+(x/(√(1+x^2 ))))/(x+(√(1+x^2 )))) −((1−(x/(√(1+x^2 ))))/(x−(√(1+x^2 ))))} =−(x/(2(1+x^2 )(√(1+x^2 )))){ ln∣x+(√(1+x^2 ))−ln∣x−(√(1+x^2 ))∣} +(1/(2(√(1+x^2 )))){ (1/(√(1+x^2 ))) +(1/(√(1+x^2 )))} ⇒g(x) =(x/(2(1+x^2 )(√(1+x^2 ))))ln∣((x+(√(1+x^2 )))/(x−(√(1+x^2 ))))∣ +(1/(1+x^2 ))

$$\left.\mathrm{4}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}{x}\:{t}\:−\mathrm{1}}\:\Rightarrow{f}^{'} \left({x}\right)\:=\:−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{xt}\:−\mathrm{1}\right)^{\mathrm{2}} }{dt}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{xt}\:−\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=−\frac{\mathrm{1}}{\mathrm{2}}{f}^{'} \left({x}\right) \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \left\{{ln}\mid{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mid−{ln}\mid{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mid\right\}\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\frac{−{x}}{\mathrm{2}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \left\{{ln}\mid{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \mid}−{ln}\mid{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mid\right\} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\left\{\:\:\:\frac{\mathrm{1}+\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:−\frac{\mathrm{1}−\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}}{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right\} \\ $$$$=−\frac{{x}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\left\{\:{ln}\mid{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−{ln}\mid{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mid\right\} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\left\{\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right\}\:\Rightarrow{g}\left({x}\right)\:=\frac{{x}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{ln}\mid\frac{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\mid \\ $$$$+\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$

Commented by maxmathsup by imad last updated on 01/Oct/18

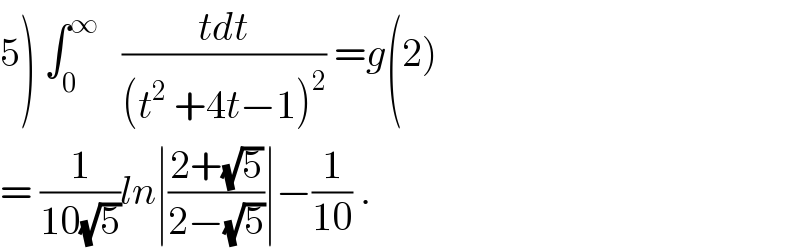
5) ∫_0 ^∞ ((tdt)/((t^2 +4t−1)^2 )) =g(2) = (1/(10(√5)))ln∣((2+(√5))/(2−(√5)))∣−(1/(10)) .

$$\left.\mathrm{5}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{tdt}}{\left({t}^{\mathrm{2}} \:+\mathrm{4}{t}−\mathrm{1}\right)^{\mathrm{2}} }\:={g}\left(\mathrm{2}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{10}\sqrt{\mathrm{5}}}{ln}\mid\frac{\mathrm{2}+\sqrt{\mathrm{5}}}{\mathrm{2}−\sqrt{\mathrm{5}}}\mid−\frac{\mathrm{1}}{\mathrm{10}}\:. \\ $$

Commented by maxmathsup by imad last updated on 01/Oct/18

g(x)=−(1/2)f^′ (x) ⇒ g(x) =(x/(4(1+x^2 )(√(1+x^2 ))))ln∣((x+(√(1+x^2 )))/(x−(√(1+x^2 ))))∣−(1/(2(1+x^2 )))

$${g}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{f}^{'} \left({x}\right)\:\Rightarrow\:{g}\left({x}\right)\:=\frac{{x}}{\mathrm{4}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{ln}\mid\frac{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\mid−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com