Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 4448 by Rasheed Soomro last updated on 29/Jan/16

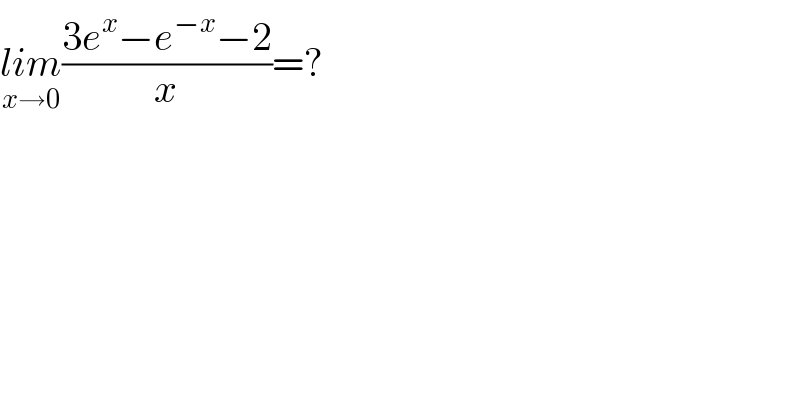
lim_(x→0) ((3e^x −e^(−x) −2)/x)=?

$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{3}{e}^{{x}} −{e}^{−{x}} −\mathrm{2}}{{x}}=? \\ $$

Answered by Yozzii last updated on 29/Jan/16

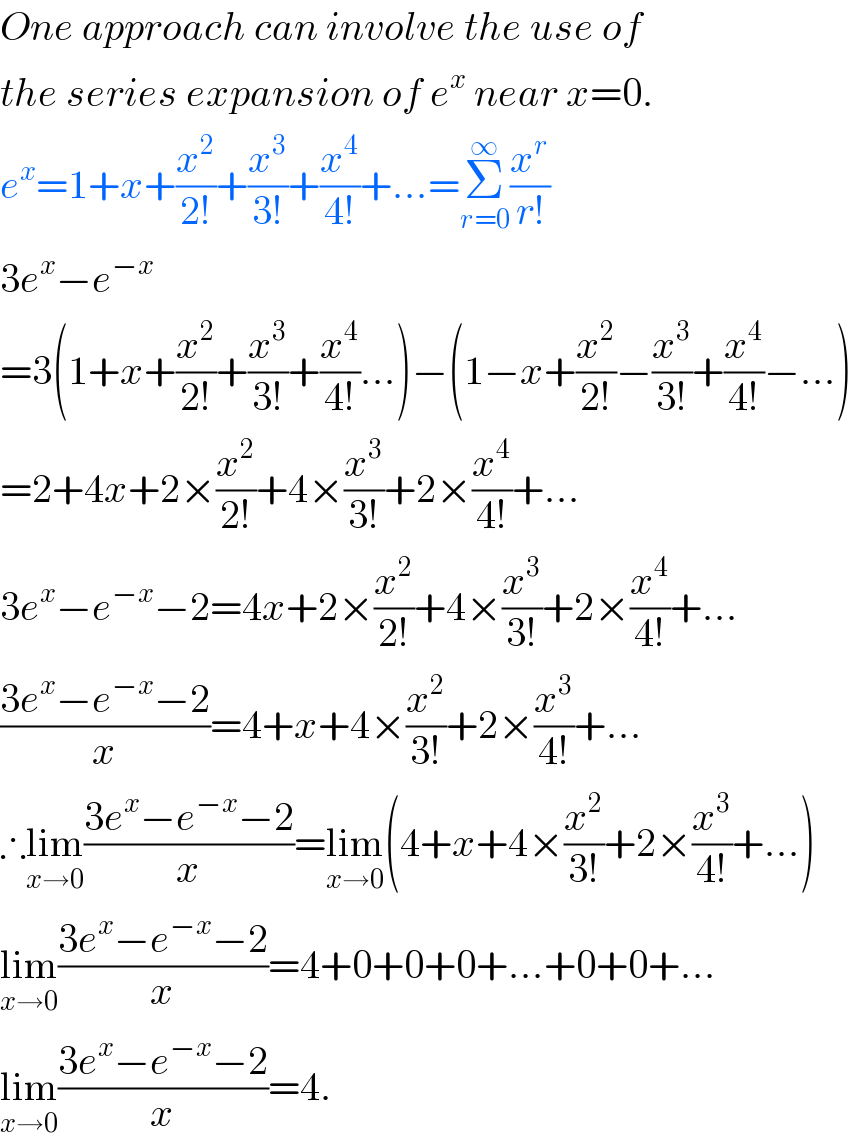
One approach can involve the use of the series expansion of e^x near x=0. e^x =1+x+(x^2 /(2!))+(x^3 /(3!))+(x^4 /(4!))+...=Σ_(r=0) ^∞ (x^r /(r!)) 3e^x −e^(−x) =3(1+x+(x^2 /(2!))+(x^3 /(3!))+(x^4 /(4!))...)−(1−x+(x^2 /(2!))−(x^3 /(3!))+(x^4 /(4!))−...) =2+4x+2×(x^2 /(2!))+4×(x^3 /(3!))+2×(x^4 /(4!))+... 3e^x −e^(−x) −2=4x+2×(x^2 /(2!))+4×(x^3 /(3!))+2×(x^4 /(4!))+... ((3e^x −e^(−x) −2)/x)=4+x+4×(x^2 /(3!))+2×(x^3 /(4!))+... ∴lim_(x→0) ((3e^x −e^(−x) −2)/x)=lim_(x→0) (4+x+4×(x^2 /(3!))+2×(x^3 /(4!))+...) lim_(x→0) ((3e^x −e^(−x) −2)/x)=4+0+0+0+...+0+0+... lim_(x→0) ((3e^x −e^(−x) −2)/x)=4.

$${One}\:{approach}\:{can}\:{involve}\:{the}\:{use}\:{of} \\ $$$${the}\:{series}\:{expansion}\:{of}\:{e}^{{x}} \:{near}\:{x}=\mathrm{0}. \\ $$$${e}^{{x}} =\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+...=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{r}} }{{r}!} \\ $$$$\mathrm{3}{e}^{{x}} −{e}^{−{x}} \\ $$$$=\mathrm{3}\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}...\right)−\left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}−...\right) \\ $$$$=\mathrm{2}+\mathrm{4}{x}+\mathrm{2}×\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\mathrm{4}×\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\mathrm{2}×\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+... \\ $$$$\mathrm{3}{e}^{{x}} −{e}^{−{x}} −\mathrm{2}=\mathrm{4}{x}+\mathrm{2}×\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\mathrm{4}×\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\mathrm{2}×\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+... \\ $$$$\frac{\mathrm{3}{e}^{{x}} −{e}^{−{x}} −\mathrm{2}}{{x}}=\mathrm{4}+{x}+\mathrm{4}×\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+\mathrm{2}×\frac{{x}^{\mathrm{3}} }{\mathrm{4}!}+... \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{e}^{{x}} −{e}^{−{x}} −\mathrm{2}}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{4}+{x}+\mathrm{4}×\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+\mathrm{2}×\frac{{x}^{\mathrm{3}} }{\mathrm{4}!}+...\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{e}^{{x}} −{e}^{−{x}} −\mathrm{2}}{{x}}=\mathrm{4}+\mathrm{0}+\mathrm{0}+\mathrm{0}+...+\mathrm{0}+\mathrm{0}+... \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{e}^{{x}} −{e}^{−{x}} −\mathrm{2}}{{x}}=\mathrm{4}. \\ $$

Answered by FilupSmith last updated on 29/Jan/16

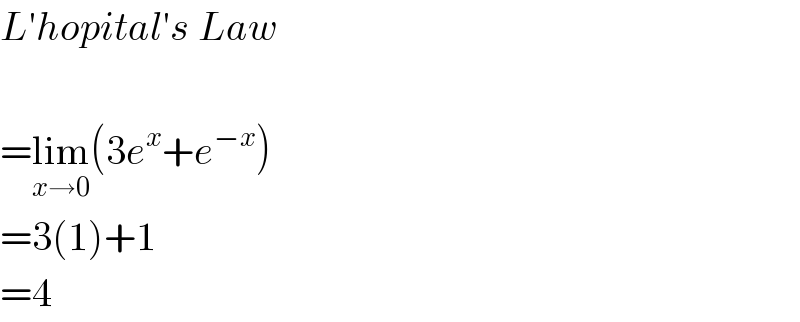
L′hopital′s Law =lim_(x→0) (3e^x +e^(−x) ) =3(1)+1 =4

$${L}'{hopital}'{s}\:{Law} \\ $$$$ \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{3}{e}^{{x}} +{e}^{−{x}} \right) \\ $$$$=\mathrm{3}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$$=\mathrm{4} \\ $$

Answered by Rasheed Soomro last updated on 29/Jan/16

Using lim_(x→0) ((e^x −1)/x)=1 lim_(x→0) ((3e^x −e^(−x) −2)/x) =lim_(x→0) ((3e^x −3−e^(−x) +1)/x) =lim_(x→0) ((3(e^x −1)−(e^(−x) −1))/x) =lim_(x→0) [((3(e^x −1))/x)+((e^(−x) −1)/(−x))] x→0 ⇒−x→0 =3lim_(x→0) ((e^x −1)/x)+lim_(−x→0) ((e^(−x) −1)/(−x)) =3(1)+1=4

$${Using}\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{3}{e}^{{x}} −{e}^{−{x}} −\mathrm{2}}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{3}{e}^{{x}} −\mathrm{3}−{e}^{−{x}} +\mathrm{1}}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{3}\left({e}^{{x}} −\mathrm{1}\right)−\left({e}^{−{x}} −\mathrm{1}\right)}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left[\frac{\mathrm{3}\left({e}^{{x}} −\mathrm{1}\right)}{{x}}+\frac{{e}^{−{x}} −\mathrm{1}}{−{x}}\right] \\ $$$${x}\rightarrow\mathrm{0}\:\Rightarrow−{x}\rightarrow\mathrm{0} \\ $$$$=\mathrm{3}\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}+\underset{−{x}\rightarrow\mathrm{0}} {{lim}}\frac{{e}^{−{x}} −\mathrm{1}}{−{x}} \\ $$$$=\mathrm{3}\left(\mathrm{1}\right)+\mathrm{1}=\mathrm{4} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com