Prove that lim_(x→0) (((1+ax)^(1/b) −1)/x) = (a/b).


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 44652 by rahul 19 last updated on 02/Oct/18

$P r o v e t h a t \lim_{x \to 0} \frac{{(1 + a x)}^{\frac{1}{b}} - 1}{x} = \frac{a}{b} .$
Commented by rahul 19 last updated on 02/Oct/18

$w i t h o u t u s i n g L - h o s p i t a l r u l e .$
Commented by maxmathsup by imad last updated on 02/Oct/18

$w e h a v e {(1 + a x)}^{\frac{1}{b}} \sim 1 + \frac{a}{b} x (x \to 0) \Rightarrow$ ${(1 + a x)}^{\frac{1}{b}} - 1 \sim \frac{a}{b} x (x \to 0) \Rightarrow \frac{{(1 + a x)}^{\frac{1}{b}} - 1}{x} \sim \frac{a}{b} \Rightarrow$ ${l i m}_{x \to 0} \frac{{(1 + a x)}^{\frac{1}{b}} - 1}{x} = \frac{a}{b} .$
Commented by rahul 19 last updated on 02/Oct/18

$t h a n k s p r o f A b d o .$
Commented by maxmathsup by imad last updated on 02/Oct/18

$y o u a r e w e l c o m e s i r .$
	Answered by math1967 last updated on 02/Oct/18
	$x^(lim) →0 ((a{(1+ax)^(1/b) −1})/(ax)) a ^(lim) x→0 (((1+ax)^(1/b) −1)/(ax)) (a/b) proved [ ^(Lim) x→0 (((1+x)^n −1)/x) ( n=any rational..) =n]$
	$\overset{l i m}{x} \to 0 \frac{a {{(1 + a x)}^{\frac{1}{b}} - 1}}{a x}$ $a \overset{l i m}{} x \to 0 \frac{{(1 + a x)}^{\frac{1}{b}} - 1}{a x}$ $\frac{a}{b} p r o v e d [\overset{L i m}{} x \to 0 \frac{{(1 + x)}^{n} - 1}{x} (n = a n y r a t i o n a l . .)$ $= n]$
	Commented by rahul 19 last updated on 02/Oct/18

	$t h a n k s s i r .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 02/Oct/18

	$t = 1 + a x x \to 0 t \to 1$ $\lim_{t \to 1} \frac{a (t^{\frac{1}{b}} - 1)}{t - 1}$ $a \times \frac{1}{b} \times {(1)}^{\frac{1}{b} - 1}$ $= \frac{a}{b}$
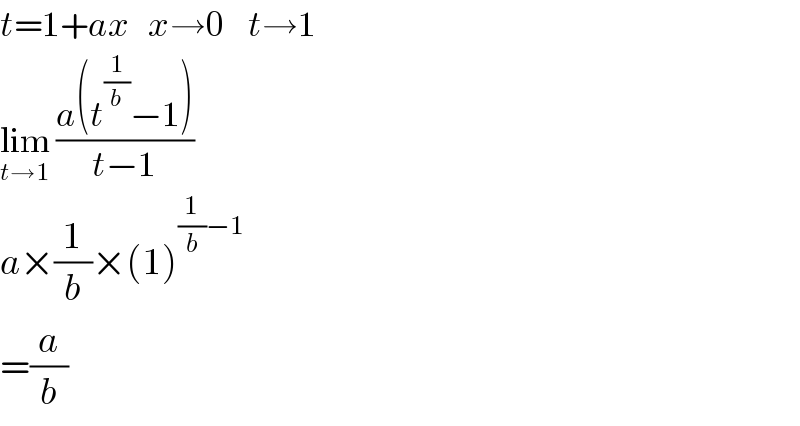
	Commented by rahul 19 last updated on 02/Oct/18

	$t h a n k s s i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum