Question Number 44676 by ajfour last updated on 03/Oct/18
Commented by ajfour last updated on 03/Oct/18
$${If}\:\:\boldsymbol{\mu}\left({x}\right)=\:\frac{\mu_{\mathrm{0}} {L}}{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}} \\ $$$${Find}\:{equation}\:{of}\:{path}\:{of}\:{light} \\ $$$${as}\:{it}\:{travels}\:{in}\:{the}\:{medium}\:{with} \\ $$$${refractive}\:{index}\:\mu\left({x}\right). \\ $$$${Hence}\:{determine}\:\boldsymbol{\beta}\:{in}\:{terms}\:{of} \\ $$$$\boldsymbol{\alpha}\:{and}\:\boldsymbol{\mu}_{\mathrm{0}} . \\ $$
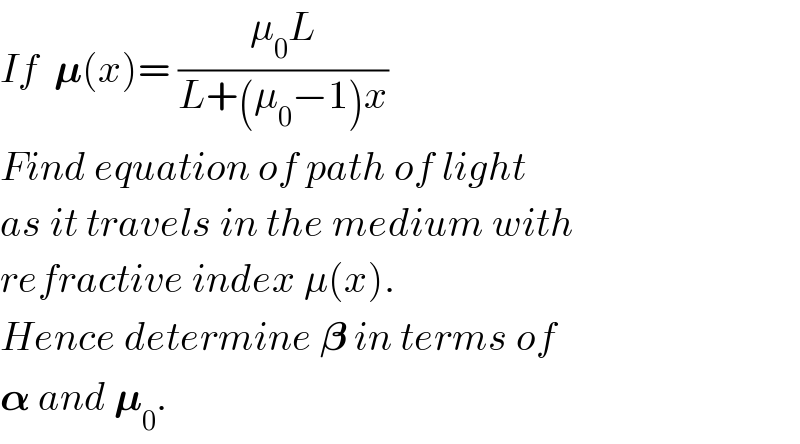
Commented by MrW3 last updated on 03/Oct/18
![𝛍(x)= ((μ_0 L)/(L+(μ_0 −1)x)) (dμ/dx)=−(((μ_0 −1)μ_0 L)/([L+(μ_0 −1)x]^2 ))=−(((μ_0 −1)μ)/(L+(μ_0 −1)x)) μ sin θ=constant sin θ (dμ/dx)+μ cos θ (dθ/dx)=0 −(((μ_0 −1)μ)/(L+(μ_0 −1)x))+μ((cos θ)/(sin θ))×(dθ/dx)=0 −(((μ_0 −1))/(L+(μ_0 −1)x))+((d(ln sin θ))/dx)=0 let Φ=ln sin θ −(((μ_0 −1))/(L+(μ_0 −1)x))+(dΦ/dx)=0 dΦ=(((μ_0 −1)dx)/(L+(μ_0 −1)x)) ∫_Φ_0 ^Φ dΦ=∫_0 ^x (((μ_0 −1)dx)/(L+(μ_0 −1)x)) Φ−Φ_0 =[ln {L+(μ_0 −1)x}]_0 ^x ln ((sin θ)/(sin θ_0 ))=ln ((L+(μ_0 −1)x)/L) sin θ=sin θ_0 ((L+(μ_0 −1)x)/L) at x=L: sin θ_1 =μ_0 sin θ_0 ⇒θ_1 =sin^(−1) (μ_0 sin θ_0 ) sin θ=sin θ_0 ((L+(μ_0 −1)x)/L)=sin θ_0 [1+(μ_0 −1)(x/L)]=λ(x) λ(x)=sin θ_0 [1+(μ_0 −1)(x/L)] dλ=sin θ_0 ((μ_0 −1)/L) dx tan θ=((sin θ)/(√(1−sin^2 θ)))=(λ/(√(1−λ^2 ))) (dy/dx)=(λ/(√(1−λ^2 ))) dy=(λ/(√(1−λ^2 )))dx=(λ/(√(1−λ^2 )))×(L/((μ_0 −1)sin θ_0 ))×dλ (((μ_0 −1)sin θ_0 )/L)dy=(λ/(√(1−λ^2 )))dλ (((μ_0 −1)sin θ_0 )/L)∫_0 ^y dy=∫_λ_0 ^λ (λ/(√(1−λ^2 )))dλ (((μ_0 −1)sin θ_0 )/L)y=−(1/2)∫_λ_0 ^λ (1/(√(1−λ^2 )))d(1−λ^2 ) (((μ_0 −1)sin θ_0 )/L)y=−[(√(1−λ^2 ))]_λ_0 ^λ =(√(1−λ_0 ^2 ))−(√(1−λ^2 )) λ_0 =sin θ_0 (((μ_0 −1)sin θ_0 )/L)y=cos θ_0 −cos θ=cos θ_0 −(√(1−sin^2 θ_0 [1+(μ_0 −1)(x/L)]^2 )) ⇒y=(L/((μ_0 −1)sin θ_0 )){cos θ_0 −(√(1−sin^2 θ_0 [1+(μ_0 −1)(x/L)]^2 ))} at x=0: μ(0)=μ_0 from air into medium sin α=μ_0 sin θ_0 ⇒sin θ_0 =((sin α)/μ_0 ) at x=L: μ(1)=1 from medium into air μ(1)×sin θ_1 =sin β ⇒β=θ_1 =sin^(−1) (μ_0 sin θ_0 )=sin^(−1) (sin α)=α ⇒y=((μ_0 L)/((μ_0 −1)sin α)){(√(1−(((sin α)/μ_0 ))^2 ))−(√(1−(((sin α)/μ_0 ))^2 [1+(μ_0 −1)(x/L)]^2 ))}](Q44682.png)
$$\boldsymbol{\mu}\left({x}\right)=\:\frac{\mu_{\mathrm{0}} {L}}{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}} \\ $$$$\frac{{d}\mu}{{dx}}=−\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mu_{\mathrm{0}} {L}}{\left[{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}\right]^{\mathrm{2}} }=−\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mu}{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}} \\ $$$$\mu\:\mathrm{sin}\:\theta={constant} \\ $$$$\mathrm{sin}\:\theta\:\frac{{d}\mu}{{dx}}+\mu\:\mathrm{cos}\:\theta\:\frac{{d}\theta}{{dx}}=\mathrm{0} \\ $$$$−\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mu}{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}}+\mu\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}×\frac{{d}\theta}{{dx}}=\mathrm{0} \\ $$$$−\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)}{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}}+\frac{{d}\left(\mathrm{ln}\:\mathrm{sin}\:\theta\right)}{{dx}}=\mathrm{0} \\ $$$${let}\:\Phi=\mathrm{ln}\:\mathrm{sin}\:\theta \\ $$$$−\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)}{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}}+\frac{{d}\Phi}{{dx}}=\mathrm{0} \\ $$$${d}\Phi=\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right){dx}}{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}} \\ $$$$\int_{\Phi_{\mathrm{0}} } ^{\Phi} {d}\Phi=\int_{\mathrm{0}} ^{{x}} \frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right){dx}}{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}} \\ $$$$\Phi−\Phi_{\mathrm{0}} =\left[\mathrm{ln}\:\left\{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}\right\}\right]_{\mathrm{0}} ^{{x}} \\ $$$$\mathrm{ln}\:\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:\theta_{\mathrm{0}} }=\mathrm{ln}\:\frac{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}}{{L}} \\ $$$$\mathrm{sin}\:\theta=\mathrm{sin}\:\theta_{\mathrm{0}} \:\frac{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}}{{L}} \\ $$$${at}\:{x}={L}: \\ $$$$\mathrm{sin}\:\theta_{\mathrm{1}} =\mu_{\mathrm{0}} \:\mathrm{sin}\:\theta_{\mathrm{0}} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\mathrm{sin}^{−\mathrm{1}} \left(\mu_{\mathrm{0}} \:\mathrm{sin}\:\theta_{\mathrm{0}} \right) \\ $$$$\mathrm{sin}\:\theta=\mathrm{sin}\:\theta_{\mathrm{0}} \:\frac{{L}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}}{{L}}=\mathrm{sin}\:\theta_{\mathrm{0}} \left[\mathrm{1}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\frac{{x}}{{L}}\right]=\lambda\left({x}\right) \\ $$$$\lambda\left({x}\right)=\mathrm{sin}\:\theta_{\mathrm{0}} \left[\mathrm{1}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\frac{{x}}{{L}}\right] \\ $$$${d}\lambda=\mathrm{sin}\:\theta_{\mathrm{0}} \:\frac{\mu_{\mathrm{0}} −\mathrm{1}}{{L}}\:{dx} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{sin}\:\theta}{\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\theta}}=\frac{\lambda}{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$$\frac{{dy}}{{dx}}=\frac{\lambda}{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$${dy}=\frac{\lambda}{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{dx}=\frac{\lambda}{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}×\frac{{L}}{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mathrm{sin}\:\theta_{\mathrm{0}} }×{d}\lambda \\ $$$$\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mathrm{sin}\:\theta_{\mathrm{0}} }{{L}}{dy}=\frac{\lambda}{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{d}\lambda \\ $$$$\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mathrm{sin}\:\theta_{\mathrm{0}} }{{L}}\int_{\mathrm{0}} ^{{y}} {dy}=\int_{\lambda_{\mathrm{0}} } ^{\lambda} \frac{\lambda}{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{d}\lambda \\ $$$$\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mathrm{sin}\:\theta_{\mathrm{0}} }{{L}}{y}=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\lambda_{\mathrm{0}} } ^{\lambda} \frac{\mathrm{1}}{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{d}\left(\mathrm{1}−\lambda^{\mathrm{2}} \right) \\ $$$$\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mathrm{sin}\:\theta_{\mathrm{0}} }{{L}}{y}=−\left[\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }\right]_{\lambda_{\mathrm{0}} } ^{\lambda} =\sqrt{\mathrm{1}−\lambda_{\mathrm{0}} ^{\mathrm{2}} }−\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$\lambda_{\mathrm{0}} =\mathrm{sin}\:\theta_{\mathrm{0}} \\ $$$$\frac{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mathrm{sin}\:\theta_{\mathrm{0}} }{{L}}{y}=\mathrm{cos}\:\theta_{\mathrm{0}} −\mathrm{cos}\:\theta=\mathrm{cos}\:\theta_{\mathrm{0}} −\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} \:\left[\mathrm{1}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\frac{{x}}{{L}}\right]^{\mathrm{2}} } \\ $$$$\Rightarrow{y}=\frac{{L}}{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mathrm{sin}\:\theta_{\mathrm{0}} }\left\{\mathrm{cos}\:\theta_{\mathrm{0}} −\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} \:\left[\mathrm{1}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\frac{{x}}{{L}}\right]^{\mathrm{2}} }\right\} \\ $$$$ \\ $$$${at}\:{x}=\mathrm{0}:\:\mu\left(\mathrm{0}\right)=\mu_{\mathrm{0}} \\ $$$${from}\:{air}\:{into}\:{medium} \\ $$$$\mathrm{sin}\:\alpha=\mu_{\mathrm{0}} \mathrm{sin}\:\theta_{\mathrm{0}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta_{\mathrm{0}} =\frac{\mathrm{sin}\:\alpha}{\mu_{\mathrm{0}} } \\ $$$${at}\:{x}={L}:\:\mu\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${from}\:{medium}\:{into}\:{air} \\ $$$$\mu\left(\mathrm{1}\right)×\mathrm{sin}\:\theta_{\mathrm{1}} =\mathrm{sin}\:\beta \\ $$$$\Rightarrow\beta=\theta_{\mathrm{1}} =\mathrm{sin}^{−\mathrm{1}} \left(\mu_{\mathrm{0}} \:\mathrm{sin}\:\theta_{\mathrm{0}} \right)=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\alpha\right)=\alpha \\ $$$$\Rightarrow{y}=\frac{\mu_{\mathrm{0}} {L}}{\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\mathrm{sin}\:\alpha}\left\{\sqrt{\mathrm{1}−\left(\frac{\mathrm{sin}\:\alpha}{\mu_{\mathrm{0}} }\right)^{\mathrm{2}} }−\sqrt{\mathrm{1}−\left(\frac{\mathrm{sin}\:\alpha}{\mu_{\mathrm{0}} }\right)^{\mathrm{2}} \:\left[\mathrm{1}+\left(\mu_{\mathrm{0}} −\mathrm{1}\right)\frac{{x}}{{L}}\right]^{\mathrm{2}} }\right\} \\ $$
Commented by ajfour last updated on 03/Oct/18
$${Awesome},\:{Sir}. \\ $$
Commented by MrW3 last updated on 03/Oct/18
$${thank}\:{you}\:{for}\:{checking}\:{sir}! \\ $$
Commented by ajfour last updated on 03/Oct/18
$${Sir},\:{our}\:{answers}\:{differ}\:{only}\:{by} \\ $$$${a}\:{factor}\:{of}\:{c}\:=\:\mathrm{sin}\:\alpha\:. \\ $$
Commented by MrW3 last updated on 03/Oct/18
$${you}\:{are}\:{right}\:{sir}.\:{I}\:{overlooked}\:\:{something}. \\ $$
Answered by ajfour last updated on 03/Oct/18
![sin α = μ_0 sin θ_0 = sin β = μsin θ =c ((dy/dx))^2 = tan^2 θ = ((sin^2 θ)/(1−sin^2 θ)) (dy/dx) = ((c/μ)/(√(1−(c^2 /μ^2 )))) = (c/(√(μ^2 −c^2 ))) y = ∫_μ_0 ^( μ) (c/(√(μ^2 −c^2 )))×((dx/dμ))dμ 𝛍= ((𝛍_0 L)/(L+(𝛍_0 −1)x)) (μ_0 −1)x = ((μ_0 L)/μ) − L ⇒ (dx/dμ) = −((μ_0 L)/(μ^2 (μ_0 −1))) y = −∫_μ_0 ^( μ) (c/(√(μ^2 −c^2 )))(((μ_0 L)/(μ^2 (μ_0 −1))))dμ = ((μ_0 cL)/(μ_0 −1))∫_μ ^( μ_0 ) (dμ/(μ^2 (√(μ^2 −c^2 )))) let μ= csec φ ⇒ dμ = csec φtan φdφ y = ((μ_0 cL)/(μ_0 −1))∫_φ ^( φ_0 ) ((csec φtan φdφ)/(c^2 sec^2 φ(ctan φ))) = ((μ_0 L)/(c(μ_0 −1))) [sin φ_0 −sin φ] y = ((𝛍_0 L)/(c(𝛍_0 −1)))[((√(𝛍_0 ^2 −c^2 ))/𝛍_0 )−((√(𝛍^2 −c^2 ))/𝛍) ] with 𝛍 = ((𝛍_0 L)/(L+(𝛍_0 −1)x)) & c=sin 𝛂 .](Q44701.png)
$$\mathrm{sin}\:\alpha\:=\:\mu_{\mathrm{0}} \mathrm{sin}\:\theta_{\mathrm{0}} =\:\mathrm{sin}\:\beta\:=\:\mu\mathrm{sin}\:\theta\:={c} \\ $$$$\:\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \:=\:\mathrm{tan}\:^{\mathrm{2}} \theta\:=\:\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$$\:\:\:\frac{{dy}}{{dx}}\:\:=\:\frac{{c}/\mu}{\sqrt{\mathrm{1}−\frac{{c}^{\mathrm{2}} }{\mu^{\mathrm{2}} }}}\:=\:\frac{{c}}{\sqrt{\mu^{\mathrm{2}} −{c}^{\mathrm{2}} }} \\ $$$$\:\:{y}\:=\:\int_{\mu_{\mathrm{0}} } ^{\:\:\mu} \frac{{c}}{\sqrt{\mu^{\mathrm{2}} −{c}^{\mathrm{2}} }}×\left(\frac{{dx}}{{d}\mu}\right){d}\mu \\ $$$$\boldsymbol{\mu}=\:\frac{\boldsymbol{\mu}_{\mathrm{0}} {L}}{{L}+\left(\boldsymbol{\mu}_{\mathrm{0}} −\mathrm{1}\right){x}} \\ $$$$\left(\mu_{\mathrm{0}} −\mathrm{1}\right){x}\:=\:\frac{\mu_{\mathrm{0}} {L}}{\mu}\:−\:{L} \\ $$$$\Rightarrow\:\:\frac{{dx}}{{d}\mu}\:=\:−\frac{\mu_{\mathrm{0}} {L}}{\mu^{\mathrm{2}} \left(\mu_{\mathrm{0}} −\mathrm{1}\right)} \\ $$$$\:\:{y}\:=\:−\int_{\mu_{\mathrm{0}} } ^{\:\:\mu} \frac{{c}}{\sqrt{\mu^{\mathrm{2}} −{c}^{\mathrm{2}} }}\left(\frac{\mu_{\mathrm{0}} {L}}{\mu^{\mathrm{2}} \left(\mu_{\mathrm{0}} −\mathrm{1}\right)}\right){d}\mu \\ $$$$\:\:\:\:\:=\:\frac{\mu_{\mathrm{0}} {cL}}{\mu_{\mathrm{0}} −\mathrm{1}}\int_{\mu} ^{\:\:\mu_{\mathrm{0}} } \frac{{d}\mu}{\mu^{\mathrm{2}} \sqrt{\mu^{\mathrm{2}} −{c}^{\mathrm{2}} }} \\ $$$${let}\:\:\mu=\:{c}\mathrm{sec}\:\phi \\ $$$$\:\:\:\Rightarrow\:\:{d}\mu\:=\:{c}\mathrm{sec}\:\phi\mathrm{tan}\:\phi{d}\phi \\ $$$$\:\:{y}\:=\:\frac{\mu_{\mathrm{0}} {cL}}{\mu_{\mathrm{0}} −\mathrm{1}}\int_{\phi} ^{\:\:\phi_{\mathrm{0}} } \:\frac{{c}\mathrm{sec}\:\phi\mathrm{tan}\:\phi{d}\phi}{{c}^{\mathrm{2}} \mathrm{sec}\:^{\mathrm{2}} \phi\left({c}\mathrm{tan}\:\phi\right)} \\ $$$$\:\:\:\:\:=\:\frac{\mu_{\mathrm{0}} {L}}{{c}\left(\mu_{\mathrm{0}} −\mathrm{1}\right)}\:\left[\mathrm{sin}\:\phi_{\mathrm{0}} −\mathrm{sin}\:\phi\right] \\ $$$$\:\:\boldsymbol{{y}}\:=\:\frac{\boldsymbol{\mu}_{\mathrm{0}} \boldsymbol{{L}}}{\boldsymbol{{c}}\left(\boldsymbol{\mu}_{\mathrm{0}} −\mathrm{1}\right)}\left[\frac{\sqrt{\boldsymbol{\mu}_{\mathrm{0}} ^{\mathrm{2}} −\boldsymbol{{c}}^{\mathrm{2}} }}{\boldsymbol{\mu}_{\mathrm{0}} }−\frac{\sqrt{\boldsymbol{\mu}^{\mathrm{2}} −\boldsymbol{{c}}^{\mathrm{2}} }}{\boldsymbol{\mu}}\:\right] \\ $$$${with}\:\boldsymbol{\mu}\:=\:\frac{\boldsymbol{\mu}_{\mathrm{0}} \boldsymbol{{L}}}{\boldsymbol{{L}}+\left(\boldsymbol{\mu}_{\mathrm{0}} −\mathrm{1}\right)\boldsymbol{{x}}}\:\:\&\:\boldsymbol{{c}}=\mathrm{sin}\:\boldsymbol{\alpha}\:. \\ $$$$ \\ $$
Commented by MrW3 last updated on 03/Oct/18
$${nice}\:{and}\:{straightforward}! \\ $$