prove that:− ∫(1/(t(√(1−t^2 ))))dt = ln(1−(√(1−t^2 )))+C


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 44781 by arvinddayama01@gmail.com last updated on 04/Oct/18

$p r o v e t h a t : - \int \frac{1}{t \sqrt{1 - t^{2}}} dt = \ln (1 - \sqrt{1 - t^{2}}) + C$
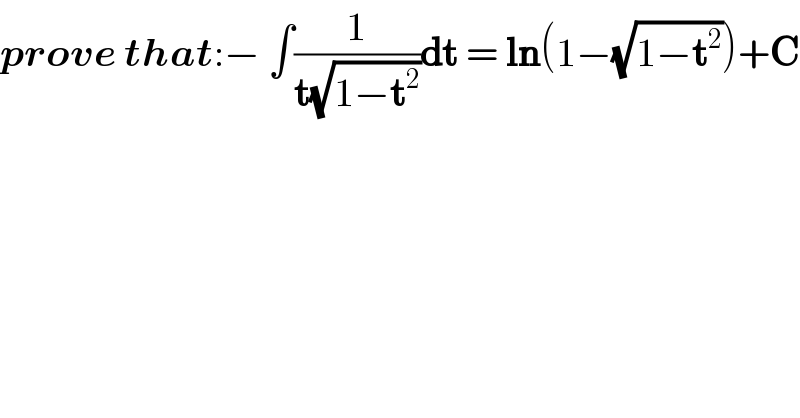
	Answered by tanmay.chaudhury50@gmail.com last updated on 04/Oct/18
	$∫((tdt)/(t^2 (√(1−t^2 )) )) k^2 =1−t^2 2kdk=−2tdt ∫((−kdk)/((1−k^2 )k)) ∫(dk/(k^2 −1)) (1/2)∫(((k+1)−(k−1))/((k+1)(k−1)))dk (1/2)∫(dk/(k−1))−(1/2)∫(dk/(k+1)) (1/2){ln(k−1)−ln(k+1)}+c (1/2){ln(((k−1)/(k+1)))}+c (1/2){ln((((√(1−t^2 )) −1)/((√(1−t^2 )) +1)))}+c←correct answer recheck of answer given RHS (d/dt){ln(1−(√(1−t^2 )) )} (1/(1−(√(1−t^2 )) ))×((0−(1/(2(√(1−t^2 )) ))×−2t)/1) (1/(1−(√(1−t^2 )) ))×(t/(√(1−t^2 ))) now recheck result obtained (d/dt)[(1/2){ln((√(1−t^2 )) −1)−ln((√(1−t^2 )) +1)}] (1/2)[{(1/((√(1−t^2 )) −1))×(1/(2(√(1−t^2 )) ))×−2t}−{(1/((√(1−t^2 )) +1))×((−2t)/(2(√(1−t^2 )) ))}] (1/2)[((−t)/((√(1−t^2 )) .((√(1−t^2 )) −1)))+(t/((√(1−t^2 )) .((√(1−t^2 )) +1)))] (t/(2(√(1−t^2 )) )){((−1)/((√(1−t_ ^2 )) −1)) +(1/((√(1−t^2 )) +1)) } (t/(2(√(1−t^2 )))){(((√(1−t)) −1−(√(1−t^2 )) −1)/((1−t^2 −1))} (1/2)×(t/(√(1−t^2 ))){((−2)/(−t^2 ))} (1/(t(√(1−t^2 )))) so attached answer in right hand side ln(1−(√(1−t^2 )) ) is not correct$
	$\int \frac{t d t}{t^{2} \sqrt{1 - t^{2}}}$ $k^{2} = 1 - t^{2} 2 k d k = - 2 t d t$ $\int \frac{- k d k}{(1 - k^{2}) k}$ $\int \frac{d k}{k^{2} - 1}$ $\frac{1}{2} \int \frac{(k + 1) - (k - 1)}{(k + 1) (k - 1)} d k$ $\frac{1}{2} \int \frac{d k}{k - 1} - \frac{1}{2} \int \frac{d k}{k + 1}$ $\frac{1}{2} {l n (k - 1) - l n (k + 1)} + c$ $\frac{1}{2} {l n (\frac{k - 1}{k + 1})} + c$ $\frac{1}{2} {l n (\frac{\sqrt{1 - t^{2}} - 1}{\sqrt{1 - t^{2}} + 1})} + c \leftarrow c o r r e c t a n s w e r$ $r e c h e c k o f a n s w e r g i v e n R H S$ $\frac{d}{d t} {l n (1 - \sqrt{1 - t^{2}})}$ $\frac{1}{1 - \sqrt{1 - t^{2}}} \times \frac{0 - \frac{1}{2 \sqrt{1 - t^{2}}} \times - 2 t}{1}$ $\frac{1}{1 - \sqrt{1 - t^{2}}} \times \frac{t}{\sqrt{1 - t^{2}}}$ $n o w r e c h e c k r e s u l t o b t a i n e d$ $\frac{d}{d t} [\frac{1}{2} {l n (\sqrt{1 - t^{2}} - 1) - l n (\sqrt{1 - t^{2}} + 1)}]$ $\frac{1}{2} [{\frac{1}{\sqrt{1 - t^{2}} - 1} \times \frac{1}{2 \sqrt{1 - t^{2}}} \times - 2 t} - {\frac{1}{\sqrt{1 - t^{2}} + 1} \times \frac{- 2 t}{2 \sqrt{1 - t^{2}}}}]$ $\frac{1}{2} [\frac{- t}{\sqrt{1 - t^{2}} . (\sqrt{1 - t^{2}} - 1)} + \frac{t}{\sqrt{1 - t^{2}} . (\sqrt{1 - t^{2}} + 1)}]$ $\frac{t}{2 \sqrt{1 - t^{2}}} {\frac{- 1}{\sqrt{1 - t_{}^{2}} - 1} + \frac{1}{\sqrt{1 - t^{2}} + 1}}$ $\frac{t}{2 \sqrt{1 - t^{2}}} {\frac{\sqrt{1 - t} - 1 - \sqrt{1 - t^{2}} - 1}{(1 - t^{2} - 1}}$ $\frac{1}{2} \times \frac{t}{\sqrt{1 - t^{2}}} {\frac{- 2}{- t^{2}}}$ $\frac{1}{t \sqrt{1 - t^{2}}}$ $s o a t t a c h e d a n s w e r i n r i g h t h a n d s i d e$ $l n (1 - \sqrt{1 - t^{2}}) i s n o t c o r r e c t$
	Commented by arvinddayama01@gmail.com last updated on 06/Oct/18

	$thanks$
	Answered by ajfour last updated on 04/Oct/18

	$l e t t = \sin θ$ $\int \frac{\cos θ d θ}{\sin θ \cos θ} = \int cosec θ d θ$ $= \ln ∣ cosec θ - \cot θ ∣ + c$ $= \ln ∣ \frac{1}{t} - \frac{\sqrt{1 - t^{2}}}{t} ∣ + c$ $= \ln ∣ 1 - \sqrt{1 - t^{2}} ∣ - \ln ∣ t ∣ + c .$
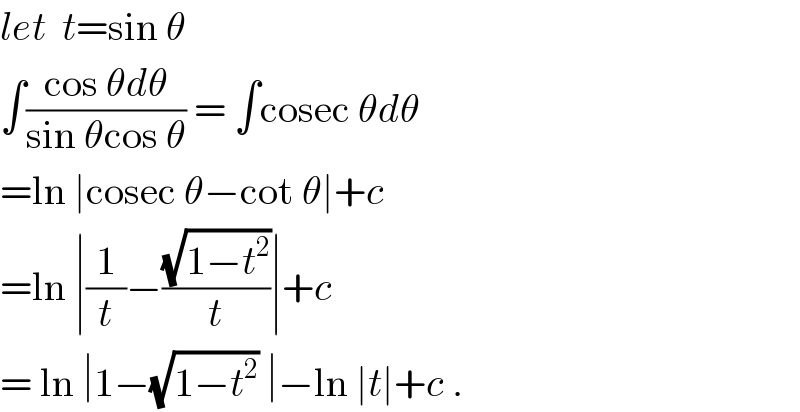
	Commented by arvinddayama01@gmail.com last updated on 06/Oct/18

	$thanks$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum