
Question and Answers Forum
Question Number 44951 by rahul 19 last updated on 06/Oct/18

Commented by rahul 19 last updated on 07/Oct/18
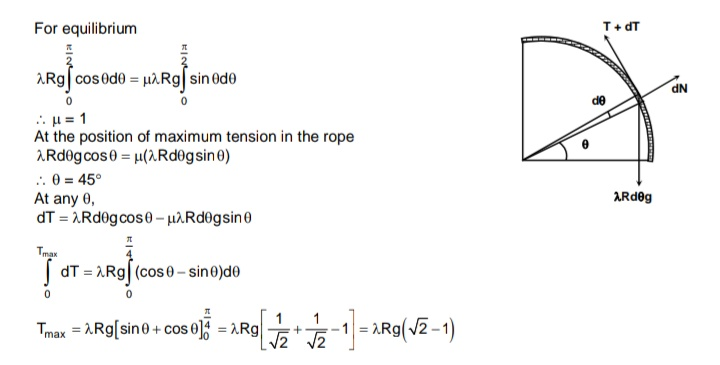
Commented by rahul 19 last updated on 07/Oct/18
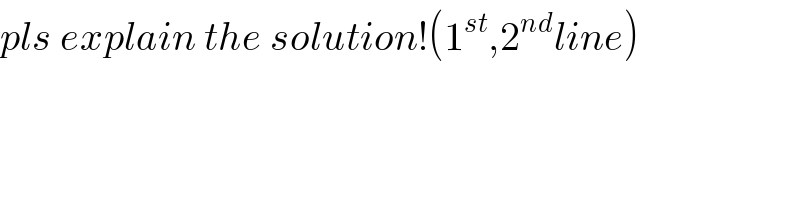
Commented by MrW3 last updated on 07/Oct/18

Answered by MrW3 last updated on 06/Oct/18
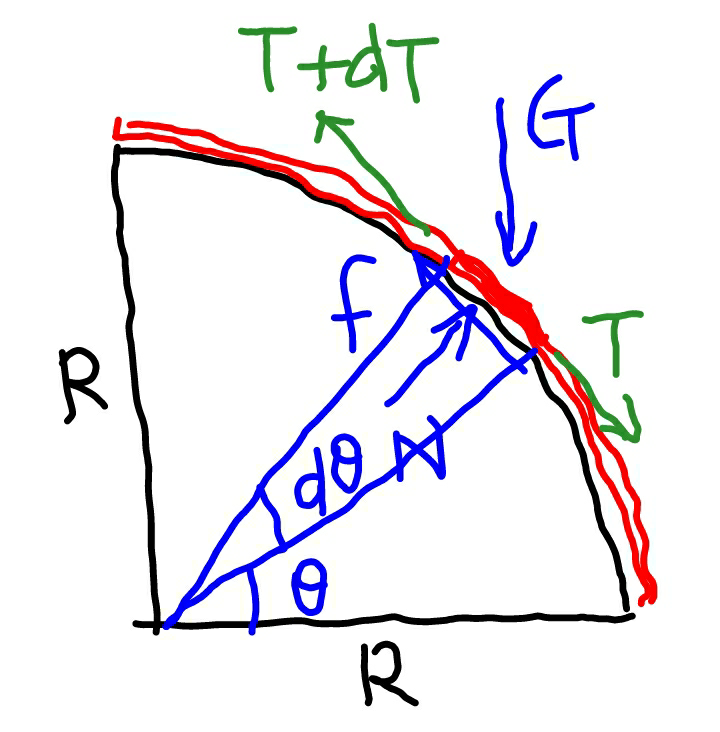
Commented by rahul 19 last updated on 07/Oct/18
sir, Ans. is AD I feel the solution is too advance for me . Anyways Thanks!!☺️��
Commented by MrW3 last updated on 07/Oct/18
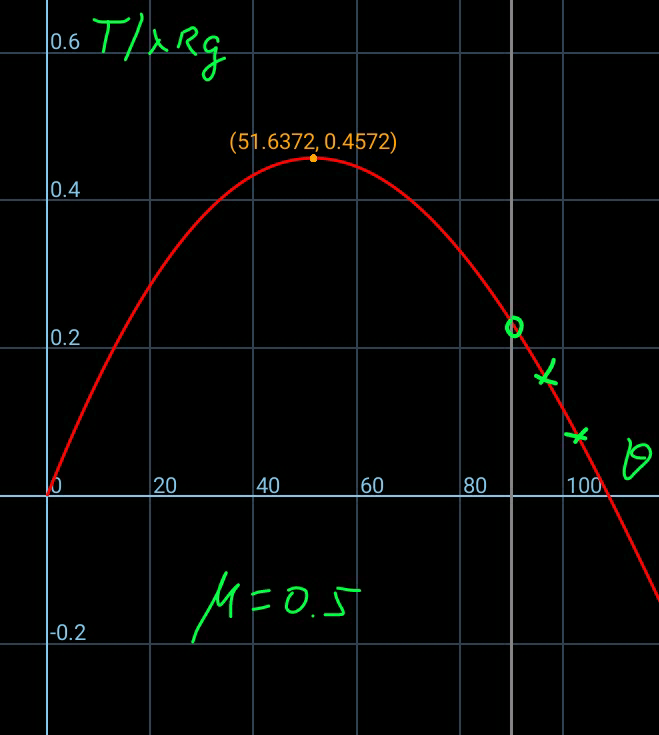
Commented by MrW3 last updated on 07/Oct/18
![G=λgds=λgRdθ N=(T/R)ds+G sin θ=(T+λgR sin θ)dθ f=μN=μ(T+λgR sin θ)dθ T+dT+f=T+G cos θ dT+μ(T+λgR sin θ)dθ=λgR cos θ dθ ⇒(dT/dθ)+μT=λgR(cos θ−μ sin θ) let T=e^(−μθ) S (dT/dθ)=−μe^(−μθ) S+e^(−μθ) (dS/dθ) −μe^(−μθ) S+e^(−μθ) (dS/dθ)+μe^(−μθ) S=λgR(cos θ−μ sin θ) e^(−μθ) (dS/dθ)=λgR(cos θ−μ sin θ) ⇒(dS/dθ)=λgRe^(μθ) (cos θ−μ sin θ) S=λgR∫e^(μθ) (cos θ−μ sin θ)dθ =((λgRe^(μθ) {2μ cos θ+(1−μ^2 )sin θ})/(1+μ^2 ))+C e^(μθ) T=((λgRe^(μθ) {2μ cos θ+(1−μ^2 )sin θ})/(1+μ^2 ))+C ⇒T=((λgR{2μ cos θ+(1−μ^2 )sin θ})/(1+μ^2 ))+Ce^(−μθ) at θ=0: T=0 ((2λgRμ)/(1+μ^2 ))+C=0 C=−((2λgRμ)/(1+μ^2 )) ⇒T=((λgR)/(1+μ^2 ))[(1−μ^2 ) sin θ+2μ(cos θ−e^(−μθ) )] the friction coeifficient is big enough if no tension force is needed to hold the rope at its topmost point. at θ=(π/2): T=^(!) 0 ((λgR)/(1+μ^2 ))(1−μ^2 −2μe^(−((μπ)/2)) )=0 ⇒1−μ^2 −2μe^(−((μπ)/2)) =0 ⇒μ≈0.7324 [Option B gives (1/(√2))=0.707] (dT/dθ)=...[(1−μ^2 )cos θ+2μ(−sin θ+μe^(−μθ) )]=0 ⇒((sin θ−μe^(−μθ) )/(cos θ))=((1−μ^2 )/(2μ)) ⇒θ in terms of μ with μ=0.7324⇒θ=41.74° ⇒T_(max) =0.353λRg [Option D gives ((√2)−1)λRg=0.414λRg]](Q44957.png)
Commented by ajfour last updated on 07/Oct/18

Commented by MrW3 last updated on 07/Oct/18

Commented by rahul 19 last updated on 07/Oct/18

Commented by MrW3 last updated on 07/Oct/18
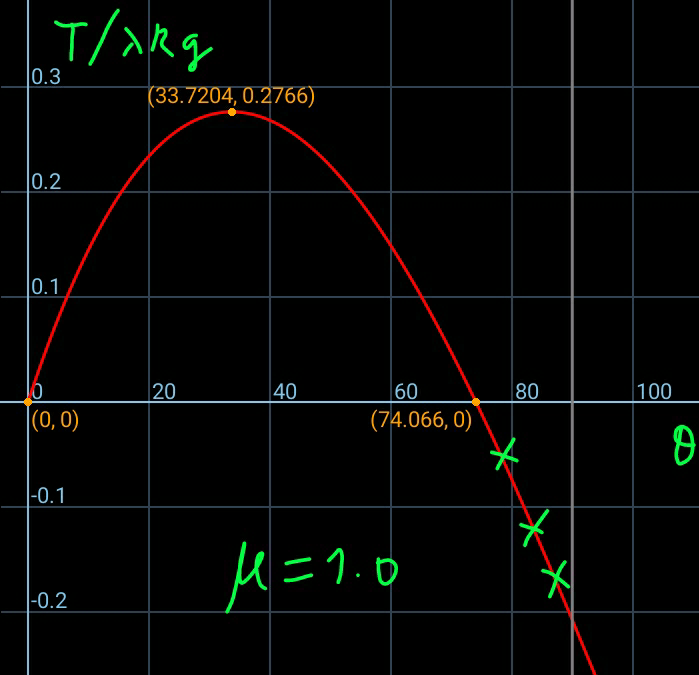
Commented by MrW3 last updated on 07/Oct/18

Commented by MrW3 last updated on 07/Oct/18

