Question Number 45020 by rahul 19 last updated on 07/Oct/18
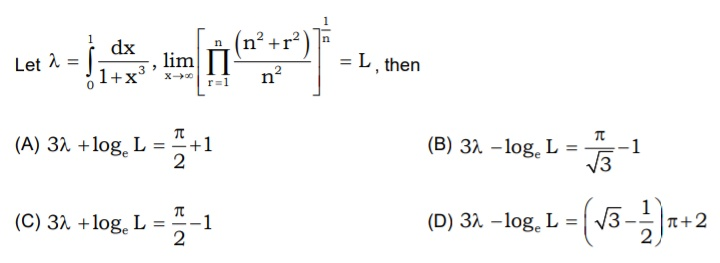
Commented by maxmathsup by imad last updated on 07/Oct/18
![let decompose F(x) =(1/(x^3 +1)) ⇒F(x)=(1/((x+1)(x^2 −x+1))) =(a/(x+1)) +((bx+c)/(x^2 −x +1)) a =lim_(x→−1) (x+1)F(x) =(1/3) lim_(x→+∞) xF(x) =0 =a+b ⇒b =−(1/3) ⇒ F(x)=(1/(3(x+1))) +((−(1/3)x+c)/(x^2 −x+1)) F(0) =(1/3) +c =1 ⇒F(x) =(2/3) ⇒F(x) =(1/(3(x+1))) +(1/3)((−x+2)/(x^2 −x+1)) ⇒ ∫_0 ^1 F(x)dx =(1/3) ∫_0 ^1 (dx/(x+1)) −(1/3) ∫_0 ^1 ((x−2)/(x^2 −x +1))dx =(1/3)ln(2) −(1/6) ∫_0 ^1 ((2x−1−3)/(x^2 −x +1))dx =((ln(2))/3) −(1/6)[ln∣x^2 −x+1∣]_0 ^1 +(1/2) ∫_0 ^1 (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)t) ((ln(2))/3) +(1/2) (4/3)∫_(−(1/(√3))) ^(1/(√3)) (1/(t^2 +1)) ((√3)/2)dt =((ln(2))/3) +(1/(√3)) { arctan((1/(√3)))+arctan((1/(√3)))} =((ln(2))/3) +(2/(√3)) (π/6) =((ln(2))/3) +(π/(3(√3))) =λ .](Q45041.png)
$${let}\:{decompose}\:{F}\left({x}\right)\:=\frac{\mathrm{1}}{{x}^{\mathrm{3}} \:+\mathrm{1}}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)} \\ $$$$=\frac{{a}}{{x}+\mathrm{1}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}} \\ $$$${a}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{3}\left({x}+\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{3}}{x}+{c}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\:+{c}\:=\mathrm{1}\:\Rightarrow{F}\left({x}\right)\:=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow{F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{3}\left({x}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{3}}\frac{−{x}+\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{x}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\mathrm{2}\right)\:−\frac{\mathrm{1}}{\mathrm{6}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{3}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}{dx} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{6}}\left[{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{4}}{\mathrm{3}}\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\:\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt}\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:\left\{\:{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)+{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right\} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\frac{\pi}{\mathrm{6}}\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:=\lambda\:. \\ $$
Commented by maxmathsup by imad last updated on 07/Oct/18
![let calculate L let A_n = {Π_(k=1) ^n (1+(k^2 /n^2 ))}^(1/n) ⇒ ln(A_n ) =(1/n) Σ_(k=1) ^n ln(1+(k^2 /n^2 )) is a Reiman sum ⇒ lim_(n→+∞) ln(A_n ) =∫_0 ^1 ln(1+x^2 )dx by parts =[xln(1+x^2 )]_0 ^1 −∫_0 ^1 x ((2x)/(1+x^2 ))dx =ln(2)−2 ∫_0 ^1 ((1+x^2 −1)/(1+x^2 ))dx =ln(2)−2 +2 ∫_0 ^1 (dx/(1+x^2 )) =ln(2)−2 +2 [arctanx]_0 ^1 =ln(2)−2+2 (π/4) =ln(2)−2+(π/2) lim_(n→+∞) A_n = e^(ln(2)−2 +(π/2)) = 2 (e^(π/2) /e^2 ) =L we have ln(L) =ln(2)−2 +(π/2) and 3λ =ln(2) +(π/(√3)) ⇒ 3λ +ln(L) =2ln(2) −2 +((1/2) +(1/(√3)))π so any answer given is correct...](Q45042.png)
$${let}\:{calculate}\:{L}\:{let}\:{A}_{{n}} =\:\left\{\prod_{{k}=\mathrm{1}} ^{{n}} \:\:\:\left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right\}^{\frac{\mathrm{1}}{{n}}} \:\Rightarrow \\ $$$${ln}\left({A}_{{n}} \right)\:=\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{ln}\left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\:{is}\:{a}\:{Reiman}\:{sum}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} {ln}\left({A}_{{n}} \right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:\:{by}\:{parts} \\ $$$$=\left[{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}\:\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}\:\left[{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} ={ln}\left(\mathrm{2}\right)−\mathrm{2}+\mathrm{2}\:\frac{\pi}{\mathrm{4}} \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}+\frac{\pi}{\mathrm{2}}\:\:{lim}_{{n}\rightarrow+\infty} {A}_{{n}} =\:{e}^{{ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\frac{\pi}{\mathrm{2}}} \:=\:\mathrm{2}\:\frac{{e}^{\frac{\pi}{\mathrm{2}}} }{{e}^{\mathrm{2}} }\:={L} \\ $$$${we}\:{have}\:{ln}\left({L}\right)\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\frac{\pi}{\mathrm{2}}\:\:{and}\:\mathrm{3}\lambda\:={ln}\left(\mathrm{2}\right)\:+\frac{\pi}{\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\mathrm{3}\lambda\:+{ln}\left({L}\right)\:=\mathrm{2}{ln}\left(\mathrm{2}\right)\:−\mathrm{2}\:+\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\pi\:\:{so}\:{any}\:{answer}\:{given}\:{is}\:{correct}... \\ $$
Commented by maxmathsup by imad last updated on 07/Oct/18
$${so}\:{any}\:{answer}\:{given}\:{is}\:{not}\:{correct}... \\ $$
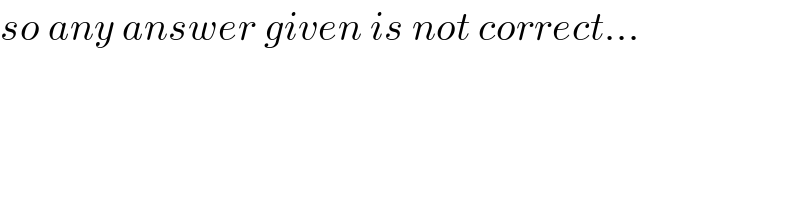
Commented by rahul 19 last updated on 08/Oct/18
thanks prof Abdo☺️
Commented by maxmathsup by imad last updated on 08/Oct/18
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Oct/18
$$\lambda=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{3}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }=\frac{{a}}{\mathrm{1}+{x}}+\frac{{bx}+{c}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} } \\ $$$$\mathrm{1}={a}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)+\left(\mathrm{1}+{x}\right)\left({bx}+{c}\right) \\ $$$$\mathrm{1}=\left({a}−{ax}+{ax}^{\mathrm{2}} \right)+\left({bx}+{c}+{bx}^{\mathrm{2}} +{cx}\right) \\ $$$$\mathrm{1}=\left({a}+{c}\right)+{x}\left(−{a}+{b}+{c}\right)+{x}^{\mathrm{2}} \left({a}+{b}\right) \\ $$$${a}+{c}=\mathrm{1} \\ $$$$−{a}+{b}+{c}=\mathrm{0} \\ $$$${a}+{b}=\mathrm{0} \\ $$$$−{a}−{a}+\mathrm{1}−{a}=\mathrm{0}\:\:\:{a}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:{b}=−\frac{\mathrm{1}}{\mathrm{3}}\:{c}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\lambda=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{{a}}{\mathrm{1}+{x}}+\frac{{bx}+{c}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }\right\}{dx} \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\frac{−\mathrm{1}}{\mathrm{3}}{x}+\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{x}+\mathrm{2}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{3}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}.{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mid{ln}\left(\mathrm{1}+{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{6}}\mid{ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left\{{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)−{tan}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}×\frac{\mathrm{2}\pi}{\mathrm{6}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${wait}\:{to}\:{find}\:{L} \\ $$$$ \\ $$
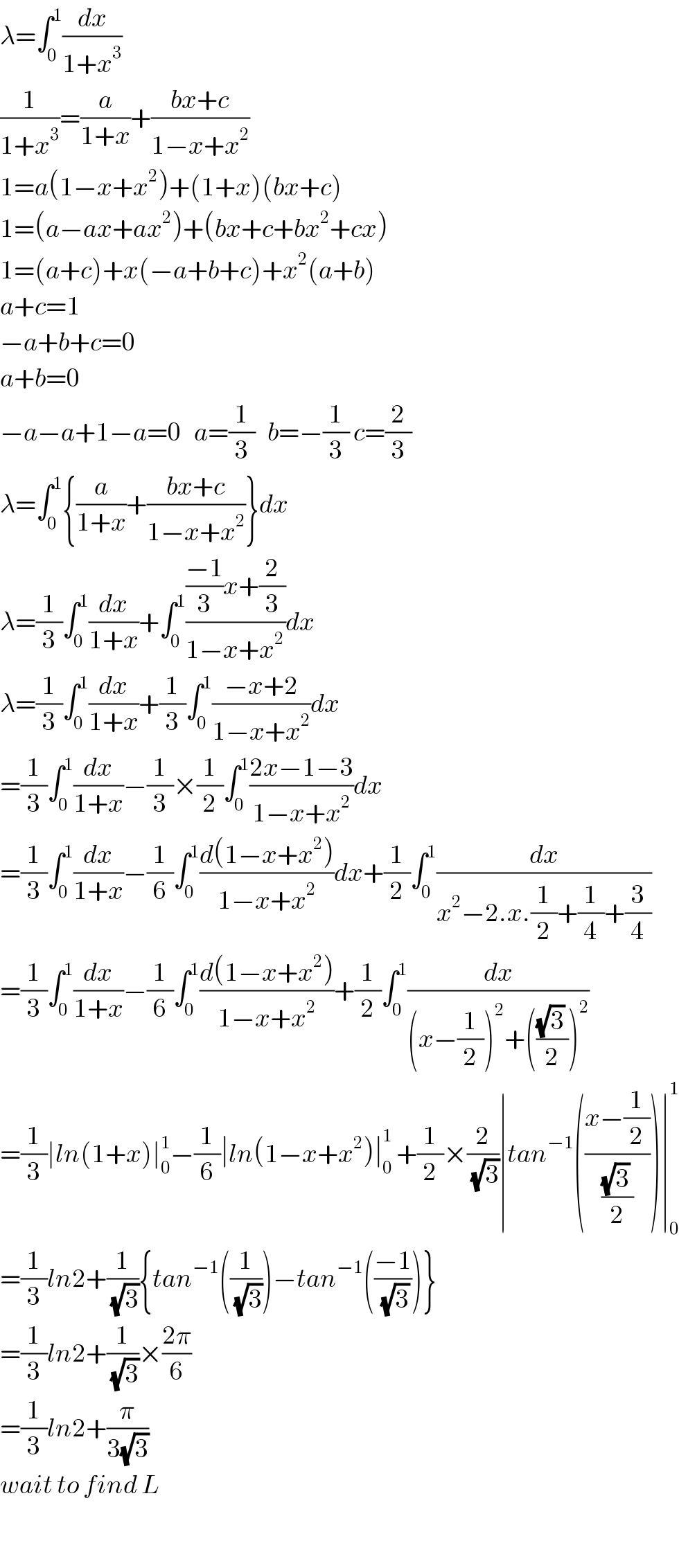
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Oct/18
![L=lim_(n→∞) [Π_(r=1) ^n (((n^2 +r^2 ))/n^2 )]^(1/n) =lim_(n→∞) [{1+((1/n))^2 }{1+((2/n))^2 }{1+((3/n))^2 }...{1+((n/n))^2 }]^(1/n) h=(1/n) lnL=lim_(h→0) h[ln(1+1^2 h^2 )+ln(1+2^2 h^2 )+ln(1+3^2 h^2 )+...+ln(1+n^2 h^2 )] lnL=∫_0 ^1 ln(1+x^2 )dx I_1 =∫ln(1+x^2 )dx =ln(1+x^2 )×x−∫((2x×x)/(1+x^2 ))dx =xln(1+x^2 )−2∫((1+x^2 −1)/(1+x^2 ))dx =xln(1+x^2 )−2∫(1−(1/(1+x^2 )))dx =xln(1+x^2 )−2[x−tan^(−1) x] lnL=∣xln(1+x^2 )−2x+2tan^(−1) x∣_0 ^1 lnL=[{ln2−2+2tan^(−1) 1}] lnL=ln2−2+2×(π/4) lnL=ln2−2+(π/2) 3λ=ln2+(π/(√3)) lnL=ln2−2+(π/2) 3λ−lnL=2+π((1/(√3))−(1/2)) pls check...](Q45030.png)
$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\underset{{r}=\mathrm{1}} {\overset{{n}} {\prod}}\frac{\left({n}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)}{{n}^{\mathrm{2}} }\right]^{\frac{\mathrm{1}}{{n}}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\left\{\mathrm{1}+\left(\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} \right\}\left\{\mathrm{1}+\left(\frac{\mathrm{2}}{{n}}\right)^{\mathrm{2}} \right\}\left\{\mathrm{1}+\left(\frac{\mathrm{3}}{{n}}\right)^{\mathrm{2}} \right\}...\left\{\mathrm{1}+\left(\frac{{n}}{{n}}\right)^{\mathrm{2}} \right\}\right]^{\frac{\mathrm{1}}{{n}}} \\ $$$${h}=\frac{\mathrm{1}}{{n}} \\ $$$${lnL}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}{h}\left[{ln}\left(\mathrm{1}+\mathrm{1}^{\mathrm{2}} {h}^{\mathrm{2}} \right)+{ln}\left(\mathrm{1}+\mathrm{2}^{\mathrm{2}} {h}^{\mathrm{2}} \right)+{ln}\left(\mathrm{1}+\mathrm{3}^{\mathrm{2}} {h}^{\mathrm{2}} \right)+...+{ln}\left(\mathrm{1}+{n}^{\mathrm{2}} {h}^{\mathrm{2}} \right)\right] \\ $$$${lnL}=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$${I}_{\mathrm{1}} =\int{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$$={ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)×{x}−\int\frac{\mathrm{2}{x}×{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}\int\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}\int\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}\left[{x}−{tan}^{−\mathrm{1}} {x}\right] \\ $$$${lnL}=\mid{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}{x}+\mathrm{2}{tan}^{−\mathrm{1}} {x}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${lnL}=\left[\left\{{ln}\mathrm{2}−\mathrm{2}+\mathrm{2}{tan}^{−\mathrm{1}} \mathrm{1}\right\}\right] \\ $$$${lnL}={ln}\mathrm{2}−\mathrm{2}+\mathrm{2}×\frac{\pi}{\mathrm{4}} \\ $$$${lnL}={ln}\mathrm{2}−\mathrm{2}+\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{3}\lambda={ln}\mathrm{2}+\frac{\pi}{\sqrt{\mathrm{3}}}\:\:\:\:\:{lnL}={ln}\mathrm{2}−\mathrm{2}+\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{3}\lambda−{lnL}=\mathrm{2}+\pi\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:\:\:{pls}\:{check}... \\ $$
Commented by rahul 19 last updated on 08/Oct/18
thanks sir!☺️