Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 45117 by rahul 19 last updated on 09/Oct/18

$$Provethat{\int }_0^1\frac{x^a-1}{\log x}dx=\log (a+1).$$

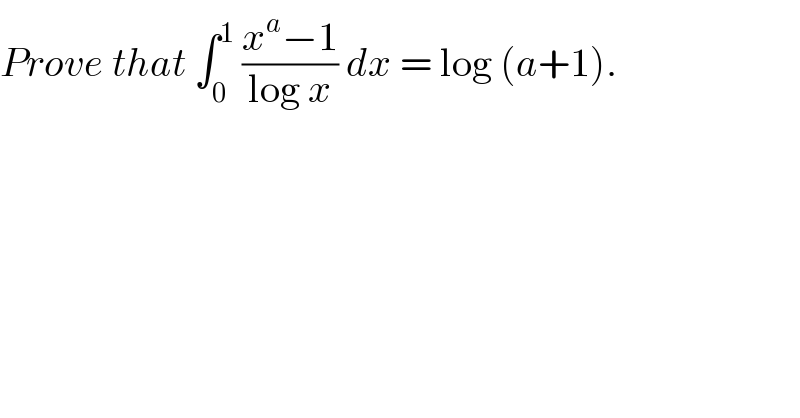
Commented by maxmathsup by imad last updated on 09/Oct/18

$$fora>-1letf\left(a\right)={\int }_0^1\frac{x^a-1}{ln\left(x\right)}dxchangementln\left(x\right)=-tgive$$$$f\left(a\right)=-{\int }_0^{+\mathrm{\infty }}\frac{e^{-at}-1}{-t}(-1)e^{-t}dt=-{\int }_0^{\mathrm{\infty }}\frac{e^{-(a+1)t}-e^{-t}}{t}dt$$$$={\int }_0^{\mathrm{\infty }}\frac{e^{-t}-e^{-(a+1)t}}{t}dt\Rightarrow f^{{}^{\prime }}\left(a\right)={\int }_0^{\mathrm{\infty }}{e}^{-(a+1)t}dt={[-\frac{1}{a+1}{e}^{-(a+1)t}]}_{t=0}^{+\mathrm{\infty }}$$$$=\frac{1}{a+1}\Rightarrow f\left(a\right)=ln\mid a+1\mid +c=ln(a+1)+cbut$$$$f\left(0\right)=0=ln\left(1\right)+c\Rightarrow c=0\Rightarrow f\left(a\right)=ln(a+1).$$$$$$$$$$

Commented by rahul 19 last updated on 09/Oct/18

thanks prof Abdo ☺️

Commented by turbo msup by abdo last updated on 09/Oct/18

$$youarewelcomesir.$$

Answered by tanmay.chaudhury50@gmail.com last updated on 09/Oct/18

$$I\left(a\right)={\int }_0^1\frac{x^a-1}{lnx}dx$$$$\frac{dI}{da}={\int }_0^1\frac{1}{lnx}\frac{\partial }{\partial a}(x^a-1)dx$$$$={\int }_0^1\frac{1}{lnx}\times x^a\times lnxdx$$$$={\int }_0^1{x}^{a}dx$$$$=\mid \frac{x^{a+1}}{a+1}{\mid }_0^1$$$$=\frac{1}{a+1}$$$$\int dI=\int \frac{da}{a+1}I=ln(a+1)$$

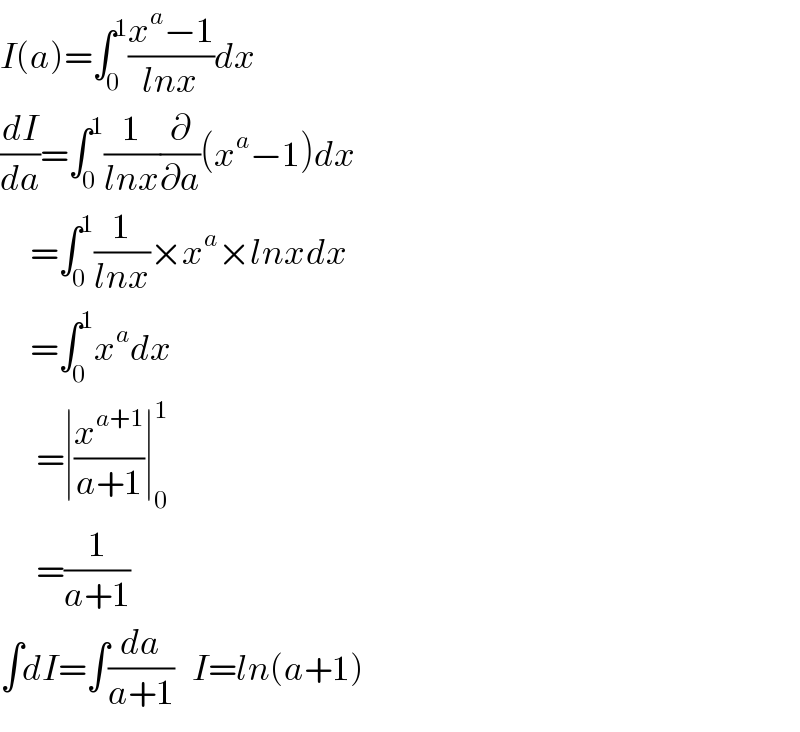
Commented by rahul 19 last updated on 09/Oct/18

Sir , how will this come to my mind first we have to differentiate!! ����

Commented by tanmay.chaudhury50@gmail.com last updated on 09/Oct/18

$$ishallpostsomeexample...thistypeintregal$$$$areadvancedintregal...frombookishallpost..$$

Commented by rahul 19 last updated on 12/Oct/18

$$Sir,plsspost2-3examples.....$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com