
Question Number 4524 by love math last updated on 05/Feb/16

$$\mathrm{3}^{\mathrm{3}{x}} +{x}^{\mathrm{2}} −\mathrm{9}>\mathrm{0} \\ $$
Commented byYozzii last updated on 05/Feb/16

$$\mathrm{27}^{{x}} >\mathrm{9}−{x}^{\mathrm{2}} \:\:\:\left(\ast\right) \\ $$ $$\left(\ast\right)\:{is}\:{true}\:{for}\:\mathrm{9}−{x}^{\mathrm{2}} \leqslant\mathrm{0}\Rightarrow{x}^{\mathrm{2}} \leqslant\mathrm{9} \\ $$ $$\Rightarrow\mid{x}\mid\geqslant\mathrm{3}.\:\mathrm{27}^{{x}} >\mathrm{0}\:\forall{x}\in\mathbb{R}\:{while}\:\mathrm{9}−{x}^{\mathrm{2}} \leqslant\mathrm{0} \\ $$ $${for}\:\mid{x}\mid\geqslant\mathrm{3}.\: \\ $$ $$ \\ $$ $$ \\ $$
Answered by Yozzii last updated on 05/Feb/16

Commented byYozzii last updated on 05/Feb/16
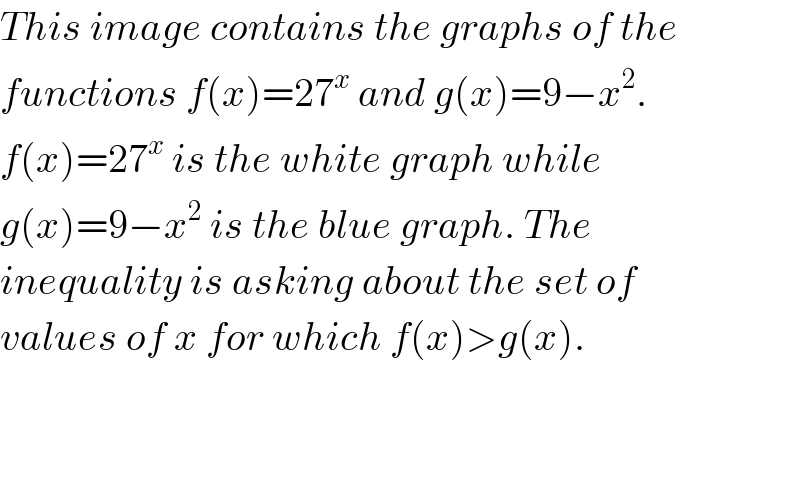
$${This}\:{image}\:{contains}\:{the}\:{graphs}\:{of}\:{the} \\ $$ $${functions}\:{f}\left({x}\right)=\mathrm{27}^{{x}} \:{and}\:{g}\left({x}\right)=\mathrm{9}−{x}^{\mathrm{2}} . \\ $$ $${f}\left({x}\right)=\mathrm{27}^{{x}} \:{is}\:{the}\:{white}\:{graph}\:{while} \\ $$ $${g}\left({x}\right)=\mathrm{9}−{x}^{\mathrm{2}} \:{is}\:{the}\:{blue}\:{graph}.\:{The}\: \\ $$ $${inequality}\:{is}\:{asking}\:{about}\:{the}\:{set}\:{of} \\ $$ $${values}\:{of}\:{x}\:{for}\:{which}\:{f}\left({x}\right)>{g}\left({x}\right). \\ $$ $$ \\ $$ $$ \\ $$
Answered by Yozzii last updated on 05/Feb/16

Commented byYozzii last updated on 05/Feb/16

$${This}\:{image}\:{shows}\:{the}\:{approximation} \\ $$ $${of}\:{the}\:{positive}\:{root}\:{of}\:{the}\:{equation} \\ $$ $$\mathrm{27}^{{x}} =\mathrm{9}−{x}^{\mathrm{2}} \:{as}\:{being}\:{x}=\mathrm{0}.\mathrm{650}.\:{From} \\ $$ $${x}>\mathrm{0}.\mathrm{650},\:\mathrm{27}^{{x}} \:{increases}\:{while}\:\mathrm{9}−{x}^{\mathrm{2}} \\ $$ $${decreases}.\:{Hence},\:\mathrm{27}^{{x}} >\mathrm{9}−{x}^{\mathrm{2}} \:{for}\: \\ $$ $${x}>\mathrm{0}.\mathrm{650}\:\:\left({approximately}\right). \\ $$ $$ \\ $$
Commented byYozzii last updated on 05/Feb/16

$${Let}\:{h}\left({x}\right)=\mathrm{27}^{{x}} +{x}^{\mathrm{2}} −\mathrm{9}. \\ $$ $$\Rightarrow{h}^{'} \left({x}\right)=\mathrm{27}^{{x}} {ln}\mathrm{27}+\mathrm{2}{x} \\ $$ $${By}\:{the}\:{Newton}−{Raphson}\:{method}, \\ $$ $${the}\:\left({n}+\mathrm{1}\right){th}\:{approximation}\:{to}\:{the} \\ $$ $${root}\:{of}\:{the}\:{equation}\:{h}\left({x}\right)=\mathrm{0},\:{given} \\ $$ $${that}\:{we}\:{have}\:{the}\:{nth}\:{approximation}, \\ $$ $${is}\:{found}\:{by}\:{the}\:{formula} \\ $$ $${x}_{{n}+\mathrm{1}} ={x}_{{n}} −\frac{{h}\left({x}_{{n}} \right)}{{h}^{'} \left({x}_{{n}} \right)}. \\ $$ $$ \\ $$ $${x}_{{n}+\mathrm{1}} =\frac{\mathrm{27}^{{x}_{{n}} } \left({x}_{{n}} {ln}\mathrm{27}−\mathrm{1}\right)+{x}_{{n}} ^{\mathrm{2}} +\mathrm{9}}{\mathrm{27}^{{x}_{{n}} } {ln}\mathrm{27}+\mathrm{2}{x}_{{n}} } \\ $$ $${Let}\:{x}_{\mathrm{1}} =\mathrm{0}.\mathrm{650}\Rightarrow{x}_{\mathrm{2}} \approx\mathrm{0}.\mathrm{65199} \\ $$ $$\Rightarrow{x}_{\mathrm{3}} \approx\mathrm{0}.\mathrm{65199}\Rightarrow{x}_{\mathrm{4}} ={x}_{\mathrm{5}} =...={x}_{{n}} \approx\mathrm{0}.\mathrm{65199} \\ $$ $${if}\:{we}\:{input}\:{successive}\:{values}\:{to}\:\mathrm{5}\:{d}.{p}. \\ $$ $$\therefore\:{x}\approx\mathrm{0}.\mathrm{652}\:{for}\:{the}\:{root}\:{so}\:{x}>\mathrm{0}.\mathrm{652}\: \\ $$ $${for}\:{f}\left({x}\right)>{g}\left({x}\right). \\ $$
Answered by Yozzii last updated on 05/Feb/16

Commented byYozzii last updated on 06/Feb/16

$${This}\:{image}\:{indicates}\:{an}\:{approximate} \\ $$ $${value}\:{of}\:{x}\:{for}\:{which}\:{f}\left({x}\right)>{g}\left({x}\right)\:{when} \\ $$ $${x}<\mathrm{0}.\:{Descending}\:{from}\:{x}\approx−\mathrm{3}.\mathrm{00} \\ $$ $${we}\:{have}\:{that}\:{f}\left({x}\right)\:{remains}\:{non}−{negative} \\ $$ $${while}\:{g}\left({x}\right)\:{falls}\:{below}\:{zero}\:{in}\:{value}. \\ $$ $${Therefore},\:{f}\left({x}\right)>{g}\left({x}\right)\:{for}\:{x}<−\mathrm{3}.\mathrm{00} \\ $$ $$\left({approximately}\right)\:{as}\:{well}.\: \\ $$ $${In}\:{all},\:\mathrm{27}^{{x}} >\mathrm{9}−{x}^{\mathrm{2}} \:{for}\:{x}>\mathrm{0}.\mathrm{652}\:{or} \\ $$ $${x}<−\mathrm{3}.\mathrm{00}\:\left({approximately}\right).\: \\ $$
