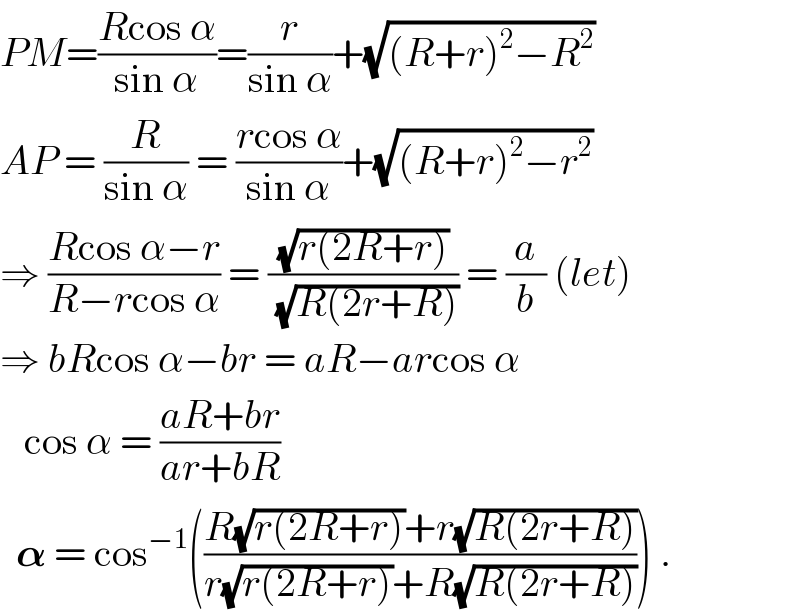Question Number 45270 by ajfour last updated on 11/Oct/18
Commented by ajfour last updated on 11/Oct/18
$${Find}\:\boldsymbol{\alpha}\:{in}\:{terms}\:{of}\:{R}\:{and}\:{r}. \\ $$
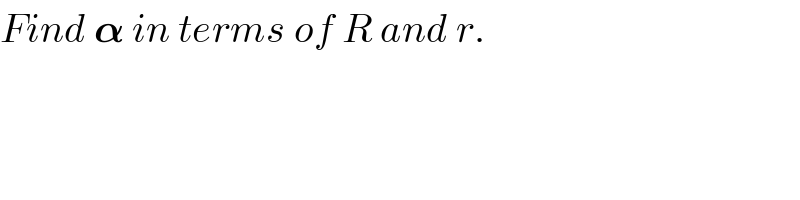
Answered by MrW3 last updated on 11/Oct/18
![PT=(r/(tan α))=((r cos α)/(sin α)) PA=(R/(sin α)) AT=PA−PT=((R−r cos α)/(sin α)) AC=R+r AC^2 =AT^2 +TC^2 (R+r)^2 =(((R−r cos α)^2 )/(sin^2 α))+r^2 (R^2 +2Rr)(1−cos^2 α)=R^2 −2Rr cos α+r^2 cos^2 α R^2 +2Rr−(R^2 +2Rr)cos^2 α=R^2 −2Rr cos α+r^2 cos^2 α (R+r)^2 cos^2 α−2Rr cos α−2Rr=0 cos α=((2Rr+(√(4R^2 r^2 +8Rr(R+r)^2 )))/(2(R+r)^2 )) cos α=((Rr+(√(Rr[(R+r)^2 +Rr])))/((R+r)^2 )) ⇒α=cos^(−1) ((Rr+(√(Rr[(R+r)^2 +Rr])))/((R+r)^2 ))](Q45273.png)
$${PT}=\frac{{r}}{\mathrm{tan}\:\alpha}=\frac{{r}\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha} \\ $$$${PA}=\frac{{R}}{\mathrm{sin}\:\alpha} \\ $$$${AT}={PA}−{PT}=\frac{{R}−{r}\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha} \\ $$$${AC}={R}+{r} \\ $$$${AC}^{\mathrm{2}} ={AT}^{\mathrm{2}} +{TC}^{\mathrm{2}} \\ $$$$\left({R}+{r}\right)^{\mathrm{2}} =\frac{\left({R}−{r}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\alpha}+{r}^{\mathrm{2}} \\ $$$$\left({R}^{\mathrm{2}} +\mathrm{2}{Rr}\right)\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha\right)={R}^{\mathrm{2}} −\mathrm{2}{Rr}\:\mathrm{cos}\:\alpha+{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha \\ $$$${R}^{\mathrm{2}} +\mathrm{2}{Rr}−\left({R}^{\mathrm{2}} +\mathrm{2}{Rr}\right)\mathrm{cos}^{\mathrm{2}} \:\alpha={R}^{\mathrm{2}} −\mathrm{2}{Rr}\:\mathrm{cos}\:\alpha+{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha \\ $$$$\left({R}+{r}\right)^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{2}{Rr}\:\mathrm{cos}\:\alpha−\mathrm{2}{Rr}=\mathrm{0} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{2}{Rr}+\sqrt{\mathrm{4}{R}^{\mathrm{2}} {r}^{\mathrm{2}} +\mathrm{8}{Rr}\left({R}+{r}\right)^{\mathrm{2}} }}{\mathrm{2}\left({R}+{r}\right)^{\mathrm{2}} } \\ $$$$\mathrm{cos}\:\alpha=\frac{{Rr}+\sqrt{{Rr}\left[\left({R}+{r}\right)^{\mathrm{2}} +{Rr}\right]}}{\left({R}+{r}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{{Rr}+\sqrt{{Rr}\left[\left({R}+{r}\right)^{\mathrm{2}} +{Rr}\right]}}{\left({R}+{r}\right)^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 11/Oct/18
$${Thank}\:{you}\:{Sir}\:! \\ $$
Answered by ajfour last updated on 11/Oct/18
$${PM}=\frac{{R}\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}=\frac{{r}}{\mathrm{sin}\:\alpha}+\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} } \\ $$$${AP}\:=\:\frac{{R}}{\mathrm{sin}\:\alpha}\:=\:\frac{{r}\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}+\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{{R}\mathrm{cos}\:\alpha−{r}}{{R}−{r}\mathrm{cos}\:\alpha}\:=\:\frac{\sqrt{{r}\left(\mathrm{2}{R}+{r}\right)}}{\sqrt{{R}\left(\mathrm{2}{r}+{R}\right)}}\:=\:\frac{{a}}{{b}}\:\left({let}\right) \\ $$$$\Rightarrow\:{bR}\mathrm{cos}\:\alpha−{br}\:=\:{aR}−{ar}\mathrm{cos}\:\alpha \\ $$$$\:\:\:\mathrm{cos}\:\alpha\:=\:\frac{{aR}+{br}}{{ar}+{bR}} \\ $$$$\:\:\boldsymbol{\alpha}\:=\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{{R}\sqrt{{r}\left(\mathrm{2}{R}+{r}\right)}+{r}\sqrt{{R}\left(\mathrm{2}{r}+{R}\right)}}{{r}\sqrt{{r}\left(\mathrm{2}{R}+{r}\right)}+{R}\sqrt{{R}\left(\mathrm{2}{r}+{R}\right)}}\right)\:. \\ $$