Question and Answers Forum
Question Number 4540 by Yozzii last updated on 06/Feb/16
![Let us define the positive number n with four digits a,b,c and d such that n=abcd with a,b,c,d∈Z, 1≤a≤9, 0≤b≤9, 0≤c≤9 and 0≤d≤9. Let us then say that a cool number is a four digit number, say n, such that the two digit numbers written as ab and cd are given by ab=r×s and cd=(r−1)×(s+1) for some non−negative integers r and s, r≠s. For example, 8081 has a=8,b=0 and 80=10×8= while c=8,d=1 and 81=9×9=(10−1)(8+1). So, for n=8081, r=10 while s=8. How many n, for 1000≤n≤9999, are cool? For n∈[1000,9999],n∈Z, how many n exist so that ab=r×s and cd=r×s+1? Call such n warm numbers.](Q4540.png)
Commented by Rasheed Soomro last updated on 06/Feb/16

Commented by Yozzii last updated on 06/Feb/16

Answered by Rasheed Soomro last updated on 08/Feb/16
![Cool Numbers Let′s attack the problem from r-s side. We have to find number of pairs (r,s) with following restrictions: ^(• ) r×s makes first two digits from left (ab) and a≥1, So, 10≤ r×s≤99............................(i) ^• (r−1)(s+1) makes last two digits 00≤ (r−1)(s+1) ≤99.................(ii) ^• r and s are non-negative integers and r≠s but as r×s≠0 ( from (i) ),so r≠0 ∧ s≠0 , i-e r and s are positve integers. r,s ∈ Z^+ with r≠s.......................(iii) From (i) 10≤ r×s≤99⇒ ((10)/r)≤s≤((99)/r) But as r,s∈Z^+ , So ⌈((10)/r)⌉≤s≤⌊((99)/r)⌋..............(iv) From (ii) 00≤ (r−1)(s+1) ≤99⇒0≤s+1≤((99)/(r−1)) ⇒−1≤s≤((99)/(r−1))−1 ⇒ −1≤s≤((100−r)/(r−1)) But since r,s∈Z^+ ,So −1≤s≤⌊((100−r)/(r−1))⌋.............(v) From (iv) &(v) Max[⌈((10)/r)⌉,−1]≤s≤Min[⌊((99)/r)⌋,⌊((100−r)/(r−1))⌋] Since r>0 ((10)/r)>−1, Max[⌈((10)/r)⌉,−1]=⌈((10)/r)⌉ ⌈((10)/r)⌉≤s≤Min[⌊((99)/r)⌋,⌊((100−r)/(r−1))⌋]....(vi) s≠r................... ....from (iii).....(vii) From (vi) & (vii) ......................................................................... ⌈((10)/r)⌉≤s≤Min[⌊((99)/r)⌋,⌊((100−r)/(r−1))⌋] ∧ s≠r...(ix) ......................................................................... Above condition determines s,if we fix r . For r=4, s is given by ⌈((10)/4)⌉≤s≤Min[⌊((99)/4)⌋,⌊((100−4)/(4−1))⌋] ⌈2.5⌉≤s≤Min[⌊24.75⌋,⌊((96)/3)⌋] 3≤s≤Min[24,32] 3≤s≤24 ∧ s≠4 s=3,5,6,7,...24 Total 21 values ................................................... r=1; s=10,11,.....99 ∣ r=31;s=1,2 r=2;s=5,6,...,49 ∣ r=32;s=1,2 r=3;s=4,5,...33 ∣ r=33;s=1,2 r=4;s=3,4^(×) ,...24 ∣ r=34;s=1,2 r=5;s=2,3,4,5^(×) ,...19 ∣ r=35;s=1 r=6;s=2,3,4,5,6^(×) ,...16 ∣r=36;s=1 r=7;s=2,3,..7^(×) ,8,...14 ∣r=37;s=1 r=8;s=2,3,...8^(×) ,...12 (38,1),(39,1)...(50,1)∣ r=9;s=2,3,....9^(×) ,10,11 r=10;s=1,2,...9 r=11;s=1,2,...8 r=12;s=1,2,...8 r=13;s=1,2,...7 r=14;s=1,2,...6 r=15;s=1,2,..,6 r=16;s=1,2...5 r=17;s=1,2,...5 Out of space](Q4547.png)
Commented by Yozzii last updated on 07/Feb/16
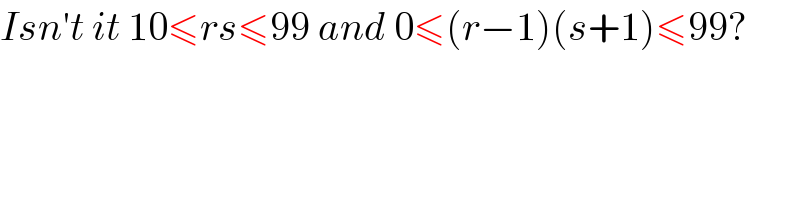
Commented by Yozzii last updated on 07/Feb/16
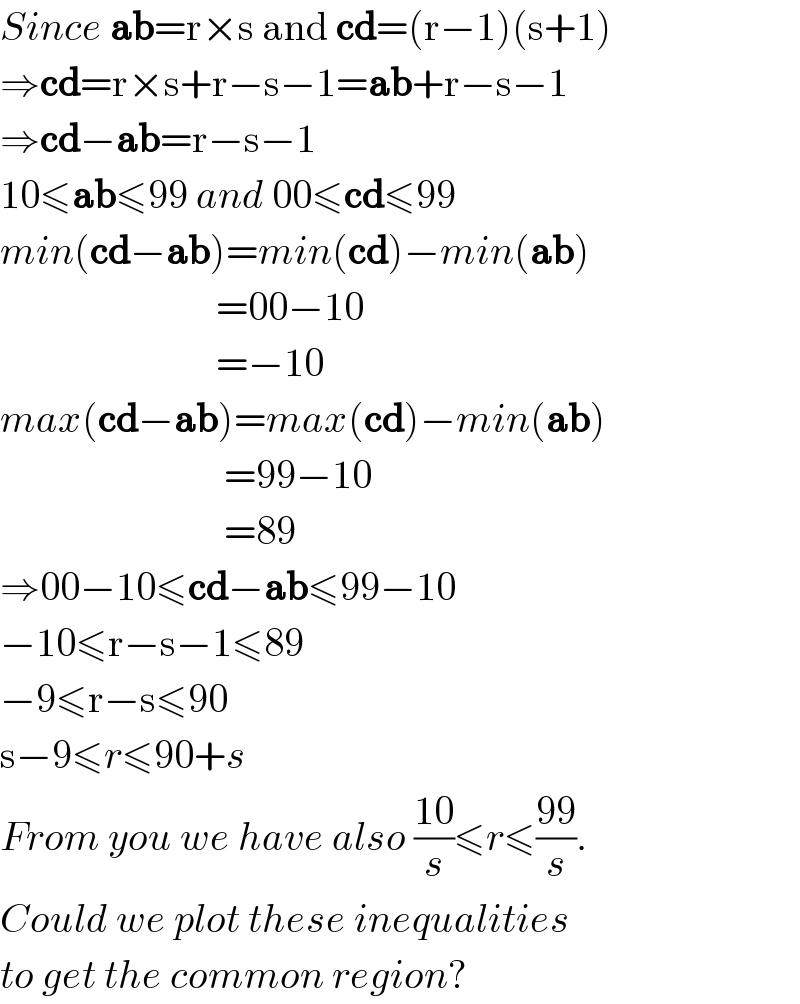
Commented by Yozzii last updated on 07/Feb/16

Commented by Yozzii last updated on 07/Feb/16

Commented by Rasheed Soomro last updated on 07/Feb/16
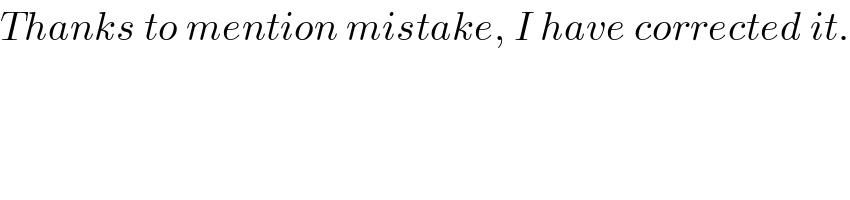
Commented by Rasheed Soomro last updated on 07/Feb/16

Commented by Rasheed Soomro last updated on 07/Feb/16

Commented by Yozzii last updated on 07/Feb/16

Commented by Rasheed Soomro last updated on 08/Feb/16