Question and Answers Forum
Question Number 45448 by MrW3 last updated on 13/Oct/18
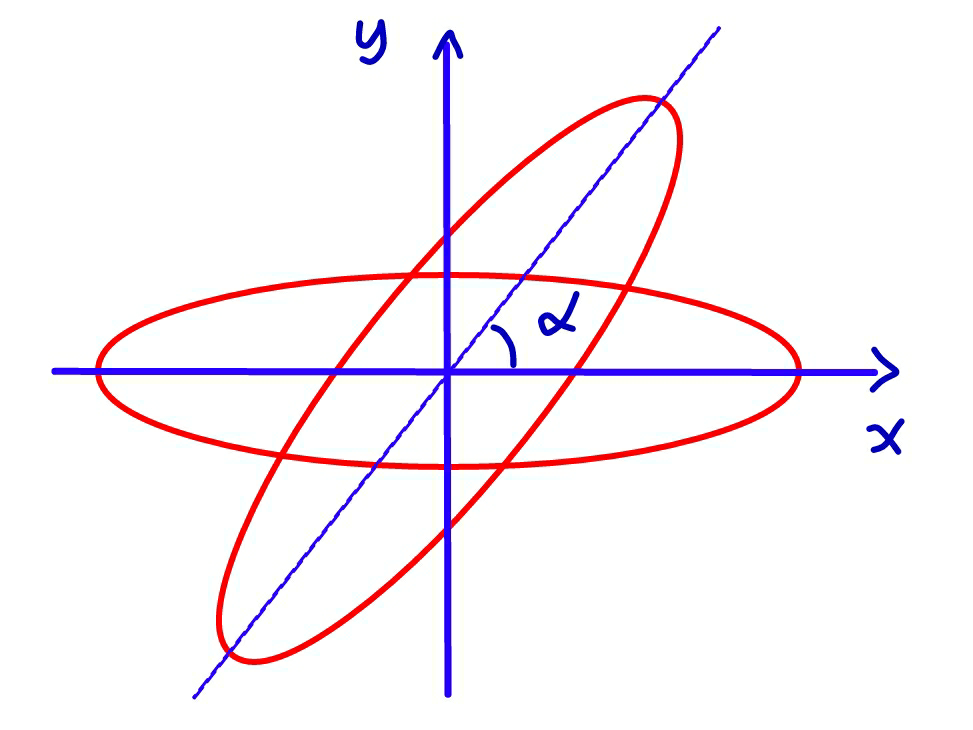
Commented by MrW3 last updated on 13/Oct/18

Commented by ajfour last updated on 13/Oct/18
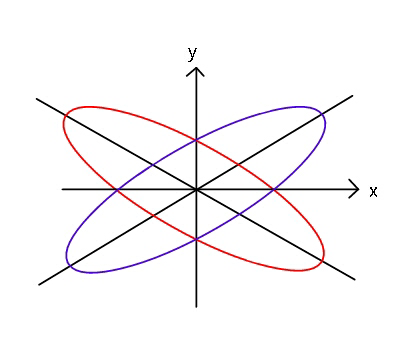
Commented by ajfour last updated on 13/Oct/18
![eq. of blue ellipse: with β=(α/2) ((r^2 cos^2 (θ−β))/a^2 )+((r^2 sin^2 (θ−β))/b^2 )=1 ⇒ r^2 =((a^2 b^2 )/(b^2 cos^2 (θ−β)+a^2 sin^2 (θ−β))) for the red one ((r^2 cos^2 (θ+β))/a^2 )+((r^2 sin^2 (θ+β))/b^2 )=1 Area of blue ellipse in I^(st) quadrant A_b = ((5πab)/(12)) Area of red ellipse in I^(st) quadrant A_r = ((πab)/(12)) A_b =∫_0 ^( π/2) ((r^2 /2)dθ) =((5πab)/(12)) ⇒ ((ab)/2)tan^(−1) [((atan (θ−β))/b)]∣_0 ^(π/2) =((5πab)/(12)) ⇒ tan^(−1) ((a/(btan β)))+tan^(−1) (((atan β)/b))= ((5π)/6) ⇔ φ+ψ = ((5π)/6) , and let m=tan β tan (φ+ψ)= −(1/(√3)) ⇒ (a/b)((1/m)+m)=−(1/(√3))(1−(a^2 /b^2 )) ⇒ ((a/b))^2 − (√3)((1/(sin βcos β)))((a/b))−1=0 ⇒ (a/b) = ((√3)/(sin α))+(√((3/(sin^2 α))+1)) .](Q45463.png)
Commented by ajfour last updated on 13/Oct/18
Commented by MrW3 last updated on 13/Oct/18