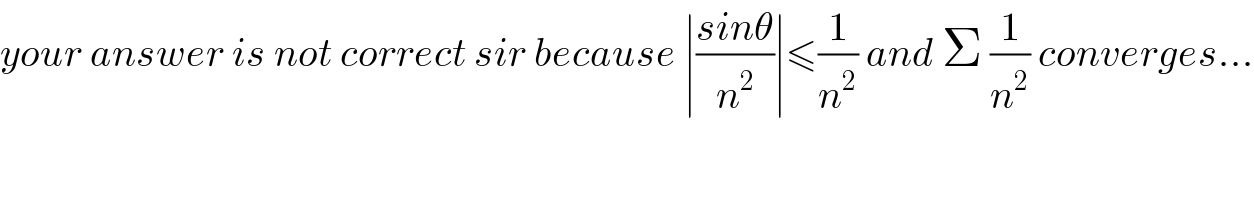calculate Σ_(n=1) ^∞ ((cos(nθ))/n^2 ) and Σ


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 45518 by maxmathsup by imad last updated on 14/Oct/18

$c a l c u l a t e \sum_{n = 1}^{\infty} \frac{c o s (n θ)}{n^{2}} a n d \sum_{n = 1}^{\infty} \frac{s i n (n θ)}{n^{2}}$
Commented by maxmathsup by imad last updated on 23/Oct/18
$we have proved that Σ_(n=1) ^∞ ((cos(nx))/n) =ln(sin((x/2))) ⇒ ∫_0 ^x (Σ_(n=1) ^∞ ((cos(nt))/n))dt =∫_0 ^x ln(sin((t/2)))dt ⇒ Σ_(n=1) ^∞ (1/n)[(1/n)sin(nt)]_0 ^x = ∫_0 ^x ln(sin((t/2)))dt⇒ Σ_(n=1) ^∞ ((sin(nx))/n^2 ) = ∫_0 ^x ln(sin((t/2)))dt=_((t/2)=u ) 2 ∫_0 ^(x/2) ln(sin(u))du also we have Σ_(n=1) ^∞ ((sin(nx))/n) =((π−x)/2) ⇒ ∫_0 ^x (Σ_(n=1) ^∞ ((sin(nt))/n))dt =∫_0 ^x ((π−t)/2)dt ⇒ Σ_(n=1) ^∞ (1/n) ∫_0 ^x sin(nt)dt =((πx)/2) −(1/2) (x^2 /2) ⇒ Σ_(n=1) ^∞ (1/n)[−(1/n)cos(nt)]_0 ^x =((πx)/2) −(x^2 /4) ⇒ Σ_(n=1) ^∞ (1/n^2 ){1−cos(nx)} =((πx)/2) −(x^2 /4) ⇒ Σ_(n=1) ^∞ ((cos(nx))/n^2 ) =(π^2 /6) −((πx)/2) +(x^2 /4) .$
$w e h a v e p r o v e d t h a t \sum_{n = 1}^{\infty} \frac{c o s (n x)}{n} = l n (s i n (\frac{x}{2})) \Rightarrow$ $\int_{0}^{x} (\sum_{n = 1}^{\infty} \frac{c o s (n t)}{n}) d t = \int_{0}^{x} l n (s i n (\frac{t}{2})) d t \Rightarrow$ $\sum_{n = 1}^{\infty} \frac{1}{n} {[\frac{1}{n} s i n (n t)]}_{0}^{x} = \int_{0}^{x} l n (s i n (\frac{t}{2})) d t \Rightarrow$ $\sum_{n = 1}^{\infty} \frac{s i n (n x)}{n^{2}} = \int_{0}^{x} l n (s i n (\frac{t}{2})) d t =_{\frac{t}{2} = u} 2 \int_{0}^{\frac{x}{2}} l n (s i n (u)) d u a l s o w e h a v e$ $\sum_{n = 1}^{\infty} \frac{s i n (n x)}{n} = \frac{π - x}{2} \Rightarrow \int_{0}^{x} (\sum_{n = 1}^{\infty} \frac{s i n (n t)}{n}) d t = \int_{0}^{x} \frac{π - t}{2} d t \Rightarrow$ $\sum_{n = 1}^{\infty} \frac{1}{n} \int_{0}^{x} s i n (n t) d t = \frac{π x}{2} - \frac{1}{2} \frac{x^{2}}{2} \Rightarrow$ $\sum_{n = 1}^{\infty} \frac{1}{n} {[- \frac{1}{n} c o s (n t)]}_{0}^{x} = \frac{π x}{2} - \frac{x^{2}}{4} \Rightarrow$ $\sum_{n = 1}^{\infty} \frac{1}{n^{2}} {1 - c o s (n x)} = \frac{π x}{2} - \frac{x^{2}}{4} \Rightarrow$ $\sum_{n = 1}^{\infty} \frac{c o s (n x)}{n^{2}} = \frac{π^{2}}{6} - \frac{π x}{2} + \frac{x^{2}}{4} .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

	$P_{n} + {i Q}_{n} = \frac{c o s n θ}{n^{2}} + i \frac{s i n n θ}{n^{2}} = \frac{e^{i n θ}}{n^{2}}$ $T_{n} = P + {i Q}_{n} = \frac{e^{i n θ}}{n^{2}}$ $S_{n} = \underset{n = 1}{\sum^{\infty}} T_{n}$ $S_{n} = \frac{e^{i θ}}{1^{2}} + \frac{e^{i 2 θ}}{2^{2}} + \frac{e^{i 3 θ}}{3^{2}} + . . . \infty$ $S_{n} = \frac{x}{1^{2}} + \frac{x^{2}}{2^{2}} + \frac{x^{3}}{3^{2}} + . . . \infty$ $w a i t p l z . . .$
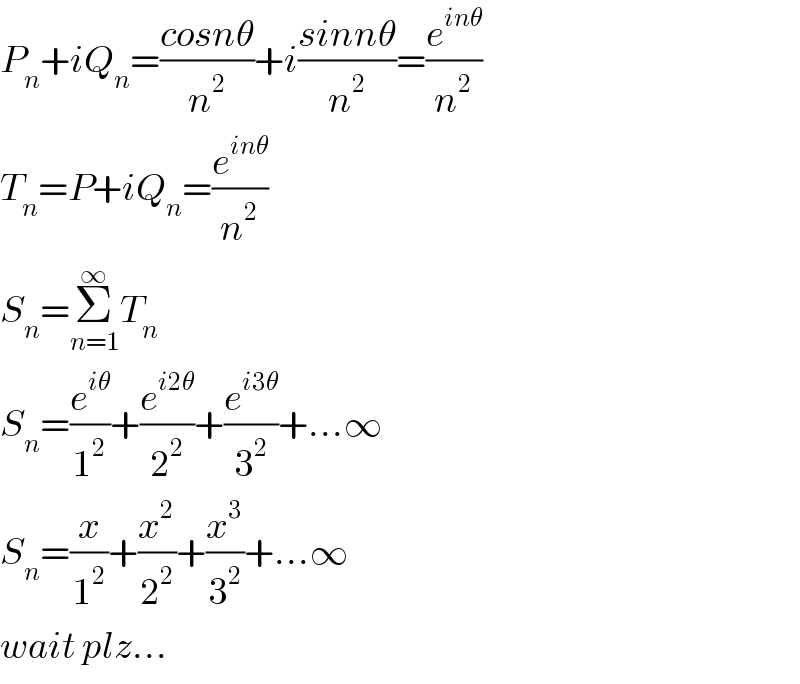
	Answered by Meritguide1234 last updated on 15/Oct/18

	Commented by maxmathsup by imad last updated on 21/Oct/18

	$y o u r a n s w e r i s n o t c o r r e c t s i r b e c a u s e ∣ \frac{s i n θ}{n^{2}} ∣⩽ \frac{1}{n^{2}} a n d Σ \frac{1}{n^{2}} c o n v e r g e s . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum