Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 4555 by FilupSmith last updated on 07/Feb/16

y=x^i x∈R i^2 =−1 is y∈C?

$${y}={x}^{{i}} \\ $$$${x}\in\mathbb{R} \\ $$$${i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{is}\:{y}\in\mathbb{C}? \\ $$

Commented by Yozzii last updated on 07/Feb/16

All known numbers are members of C since C=R∪{wholly complex numbers}. C is unbounded and open.

$${All}\:{known}\:{numbers}\:{are}\:{members}\:{of} \\ $$$$\mathbb{C}\:{since}\:\mathbb{C}=\mathbb{R}\cup\left\{{wholly}\:{complex}\:{numbers}\right\}. \\ $$$$\mathbb{C}\:{is}\:{unbounded}\:{and}\:{open}.\: \\ $$$$ \\ $$

Commented by FilupSmith last updated on 07/Feb/16

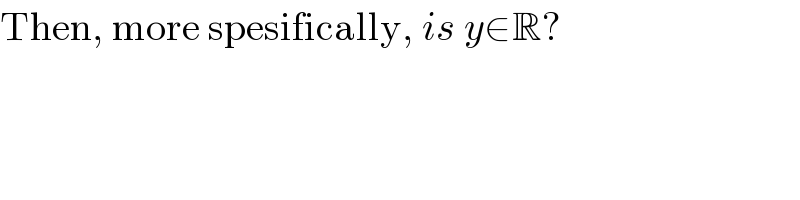
Then, more spesifically, is y∈R?

$$\mathrm{Then},\:\mathrm{more}\:\mathrm{spesifically},\:{is}\:{y}\in\mathbb{R}? \\ $$

Commented by Yozzii last updated on 07/Feb/16

y could be real or complex. x∈R If x>0, x=e^(lnx) ⇒x^i =e^(ilnx) =y x^i =cos(lnx)+isin(lnx) If y=x^i ∈R⇒sin(lnx)=0 ⇒lnx=nπ⇒x=e^(nπ) (n∈Z). If y=x^i ∈{wholly complex}⇒cos(lnx)=0 ∴lnx=2nπ±0.5π⇒x=e^(2nπ±0.5) (n∈Z). For x>0, x≠e^(nπ) and x≠e^(2nπ±0.5) , y∈C. If x<0 let x=−a, a>0 (a∈R) ⇒x=−a=a(cosπ+isinπ)=ae^(πi) x=e^(ln(ae^(iπ) )) =e^(lna+iπ) ⇒x^i =e^(ilna+i^2 π) =e^(ilna−π) =e^(−π) (cos(lna)+isin(lna)) So, similarly for x<0, y∈R or y∈C. I don′t think y is defined for x=0.

$${y}\:{could}\:{be}\:{real}\:{or}\:{complex}. \\ $$$${x}\in\mathbb{R} \\ $$$${If}\:{x}>\mathrm{0},\:{x}={e}^{{lnx}} \Rightarrow{x}^{{i}} ={e}^{{ilnx}} ={y} \\ $$$${x}^{{i}} ={cos}\left({lnx}\right)+{isin}\left({lnx}\right) \\ $$$${If}\:{y}={x}^{{i}} \in\mathbb{R}\Rightarrow{sin}\left({lnx}\right)=\mathrm{0} \\ $$$$\Rightarrow{lnx}={n}\pi\Rightarrow{x}={e}^{{n}\pi} \:\left({n}\in\mathbb{Z}\right). \\ $$$${If}\:{y}={x}^{{i}} \in\left\{{wholly}\:{complex}\right\}\Rightarrow{cos}\left({lnx}\right)=\mathrm{0} \\ $$$$\therefore{lnx}=\mathrm{2}{n}\pi\pm\mathrm{0}.\mathrm{5}\pi\Rightarrow{x}={e}^{\mathrm{2}{n}\pi\pm\mathrm{0}.\mathrm{5}} \:\left({n}\in\mathbb{Z}\right). \\ $$$${For}\:{x}>\mathrm{0},\:{x}\neq{e}^{{n}\pi} \:{and}\:{x}\neq{e}^{\mathrm{2}{n}\pi\pm\mathrm{0}.\mathrm{5}} ,\:{y}\in\mathbb{C}.\: \\ $$$$ \\ $$$${If}\:{x}<\mathrm{0}\:{let}\:{x}=−{a},\:{a}>\mathrm{0}\:\:\left({a}\in\mathbb{R}\right) \\ $$$$\Rightarrow{x}=−{a}={a}\left({cos}\pi+{isin}\pi\right)={ae}^{\pi{i}} \\ $$$${x}={e}^{{ln}\left({ae}^{{i}\pi} \right)} ={e}^{{lna}+{i}\pi} \\ $$$$\Rightarrow{x}^{{i}} ={e}^{{ilna}+{i}^{\mathrm{2}} \pi} ={e}^{{ilna}−\pi} ={e}^{−\pi} \left({cos}\left({lna}\right)+{isin}\left({lna}\right)\right) \\ $$$${So},\:{similarly}\:{for}\:{x}<\mathrm{0},\:{y}\in\mathbb{R}\:{or}\:{y}\in\mathbb{C}. \\ $$$$ \\ $$$${I}\:{don}'{t}\:{think}\:{y}\:{is}\:{defined}\:{for}\:{x}=\mathrm{0}. \\ $$$$ \\ $$$$ \\ $$

Commented by Yozzii last updated on 07/Feb/16

Let′s consider the general form y=(a+bi)^(c+id) where i^2 =−1, a,b,c,d∈R, and if a=b, then a≠0 for if a=b=0, y is undefined since arg(0) is undefined. In modulus−polar form, a+bi=re^(iθ) where r=(√(a^2 +b^2 )) ,r>0, and θ , −π<θ≤π, is the principal argument of the complex number a+bi. e is Euler′s constant. ∴ y=(re^(iθ) )^(c+id ) =r^(c+id) e^(iθ(c+id)) y=r^c (r^d )^i e^(ciθ−θd) =r^c e^(−θd) (r^d e^(cθ) )^i =nx^i where n=r^c e^(−θd) >0, x=r^d e^(cθ) >0, n,x∈R. y=n(e^(lnx) )^i =ne^(ilnx) =n(cos(lnx)+isin(lnx)) y=ncos(lnx)+insin(lnx) From this we know that ∣y∣=n=r^c e^(−θd) and arg(y)=lnx=ln(r^d e^(cθ) )=cθ+dlnr. (1) If y is real⇒nsin(lnx)=0 ⇒lnx=tπ⇒x=e^(tπ) , t∈Z. ∴ y=ncos(lnx)=r^c e^(−θd) cos(lne^(tπ) ) y=(a^2 +b^2 )^(c/2) e^(−dθ) costπ y=(−1)^t e^(−dθ) (a^2 +b^2 )^(c/2) ,t∈Z. {Since x=r^d e^(cθ) and x=e^(tπ) ⇒e^(tπ) =r^d e^(cθ) ∴tπ=dlnr+cθ t=((dlnr+cθ)/π)∈Z Is it necessary for t∈Z that r=1?} (2)If y is wholly complex⇒ ncos(lnx)=0 ⇒lnx=2tπ±0.5π⇒x=e^(2tπ±0.5π) ,t∈Z ∴ y=nisin(2tπ±0.5π) y=ni(sin2tπcos0.5π±sin0.5πcos2tπ) y=±ni=±r^c e^(−θd) i x=r^d e^(cθ) ∴ r^d e^(cθ) =e^(2tπ±0.5π) dlnr+cθ=2tπ±0.5π t=((dlnr+cθ±0.5π)/(2π))∈Z (3)For r^d e^(cθ) ≠e^((2t±0.5)π) ,e^(qπ) where t,q∈Z, Im(y)≠0 and Re(y)≠0 and has the form y=r^c e^(−dθ) (cos(cθ+dlnr)+isin(cθ+dlnr)) Re(y)=(a^2 +b^2 )^(c/2) e^(−dθ) cos(cθ+(1/2)dln(a^2 +b^2 )) Im(y)=(a^2 +b^2 )^(c/2) e^(−dθ) sin(cθ+(1/2)dln(a^2 +b^2 ))

$${Let}'{s}\:{consider}\:{the}\:{general}\:{form}\: \\ $$$${y}=\left({a}+{bi}\right)^{{c}+{id}} \:{where}\:{i}^{\mathrm{2}} =−\mathrm{1}, \\ $$$${a},{b},{c},{d}\in\mathbb{R},\:{and}\:{if}\:{a}={b},\:{then}\:{a}\neq\mathrm{0}\:{for} \\ $$$${if}\:{a}={b}=\mathrm{0},\:{y}\:{is}\:{undefined}\:{since}\:{arg}\left(\mathrm{0}\right) \\ $$$${is}\:{undefined}.\: \\ $$$$ \\ $$$${In}\:{modulus}−{polar}\:{form}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}+{bi}={re}^{{i}\theta} \\ $$$${where}\:{r}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:,{r}>\mathrm{0},\:{and}\:\theta\:,\:−\pi<\theta\leqslant\pi,\:{is}\:{the}\: \\ $$$${principal}\:{argument}\:{of}\:{the}\:{complex}\:{number} \\ $$$${a}+{bi}.\:{e}\:{is}\:{Euler}'{s}\:{constant}. \\ $$$$\therefore\:{y}=\left({re}^{{i}\theta} \right)^{{c}+{id}\:} ={r}^{{c}+{id}} {e}^{{i}\theta\left({c}+{id}\right)} \\ $$$${y}={r}^{{c}} \left({r}^{{d}} \right)^{{i}} {e}^{{ci}\theta−\theta{d}} ={r}^{{c}} {e}^{−\theta{d}} \left({r}^{{d}} {e}^{{c}\theta} \right)^{{i}} ={nx}^{{i}} \\ $$$${where}\:{n}={r}^{{c}} {e}^{−\theta{d}} >\mathrm{0},\:{x}={r}^{{d}} {e}^{{c}\theta} >\mathrm{0}, \\ $$$${n},{x}\in\mathbb{R}. \\ $$$${y}={n}\left({e}^{{lnx}} \right)^{{i}} ={ne}^{{ilnx}} ={n}\left({cos}\left({lnx}\right)+{isin}\left({lnx}\right)\right) \\ $$$${y}={ncos}\left({lnx}\right)+{insin}\left({lnx}\right) \\ $$$${From}\:{this}\:{we}\:{know}\:{that}\:\mid{y}\mid={n}={r}^{{c}} {e}^{−\theta{d}} \\ $$$${and}\:{arg}\left({y}\right)={lnx}={ln}\left({r}^{{d}} {e}^{{c}\theta} \right)={c}\theta+{dlnr}. \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{If}\:{y}\:{is}\:{real}\Rightarrow{nsin}\left({lnx}\right)=\mathrm{0} \\ $$$$\Rightarrow{lnx}={t}\pi\Rightarrow{x}={e}^{{t}\pi} ,\:{t}\in\mathbb{Z}.\: \\ $$$$\therefore\:{y}={ncos}\left({lnx}\right)={r}^{{c}} {e}^{−\theta{d}} {cos}\left({lne}^{{t}\pi} \right) \\ $$$${y}=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\frac{{c}}{\mathrm{2}}} {e}^{−{d}\theta} {cost}\pi \\ $$$${y}=\left(−\mathrm{1}\right)^{{t}} {e}^{−{d}\theta} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{{c}/\mathrm{2}} ,{t}\in\mathbb{Z}. \\ $$$$\left\{{Since}\:{x}={r}^{{d}} {e}^{{c}\theta} \:{and}\:{x}={e}^{{t}\pi} \Rightarrow{e}^{{t}\pi} ={r}^{{d}} {e}^{{c}\theta} \right. \\ $$$$\therefore{t}\pi={dlnr}+{c}\theta \\ $$$${t}=\frac{{dlnr}+{c}\theta}{\pi}\in\mathbb{Z} \\ $$$$\left.{Is}\:{it}\:{necessary}\:{for}\:{t}\in\mathbb{Z}\:{that}\:{r}=\mathrm{1}?\right\} \\ $$$$ \\ $$$$\left(\mathrm{2}\right){If}\:{y}\:{is}\:{wholly}\:{complex}\Rightarrow\:{ncos}\left({lnx}\right)=\mathrm{0} \\ $$$$\Rightarrow{lnx}=\mathrm{2}{t}\pi\pm\mathrm{0}.\mathrm{5}\pi\Rightarrow{x}={e}^{\mathrm{2}{t}\pi\pm\mathrm{0}.\mathrm{5}\pi} ,{t}\in\mathbb{Z} \\ $$$$\therefore\:{y}={nisin}\left(\mathrm{2}{t}\pi\pm\mathrm{0}.\mathrm{5}\pi\right) \\ $$$${y}={ni}\left({sin}\mathrm{2}{t}\pi{cos}\mathrm{0}.\mathrm{5}\pi\pm{sin}\mathrm{0}.\mathrm{5}\pi{cos}\mathrm{2}{t}\pi\right) \\ $$$${y}=\pm{ni}=\pm{r}^{{c}} {e}^{−\theta{d}} {i} \\ $$$${x}={r}^{{d}} {e}^{{c}\theta} \:\therefore\:{r}^{{d}} {e}^{{c}\theta} ={e}^{\mathrm{2}{t}\pi\pm\mathrm{0}.\mathrm{5}\pi} \\ $$$${dlnr}+{c}\theta=\mathrm{2}{t}\pi\pm\mathrm{0}.\mathrm{5}\pi \\ $$$${t}=\frac{{dlnr}+{c}\theta\pm\mathrm{0}.\mathrm{5}\pi}{\mathrm{2}\pi}\in\mathbb{Z} \\ $$$$\left(\mathrm{3}\right){For}\:{r}^{{d}} {e}^{{c}\theta} \neq{e}^{\left(\mathrm{2}{t}\pm\mathrm{0}.\mathrm{5}\right)\pi} ,{e}^{{q}\pi} \:{where} \\ $$$${t},{q}\in\mathbb{Z},\:{Im}\left({y}\right)\neq\mathrm{0}\:{and}\:{Re}\left({y}\right)\neq\mathrm{0}\:{and}\:{has}\:{the}\:{form}\: \\ $$$${y}={r}^{{c}} {e}^{−{d}\theta} \left({cos}\left({c}\theta+{dlnr}\right)+{isin}\left({c}\theta+{dlnr}\right)\right) \\ $$$${Re}\left({y}\right)=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\frac{{c}}{\mathrm{2}}} {e}^{−{d}\theta} {cos}\left({c}\theta+\frac{\mathrm{1}}{\mathrm{2}}{dln}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\right) \\ $$$${Im}\left({y}\right)=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\frac{{c}}{\mathrm{2}}} {e}^{−{d}\theta} {sin}\left({c}\theta+\frac{\mathrm{1}}{\mathrm{2}}{dln}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\right) \\ $$$$ \\ $$

Commented by FilupSmith last updated on 07/Feb/16

Wow! This is amazing and very interesting! I love it!

$$\mathrm{Wow}!\:\mathrm{This}\:\mathrm{is}\:\mathrm{amazing}\:\mathrm{and}\:\mathrm{very}\:\mathrm{interesting}! \\ $$$$\mathrm{I}\:\mathrm{love}\:\mathrm{it}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com