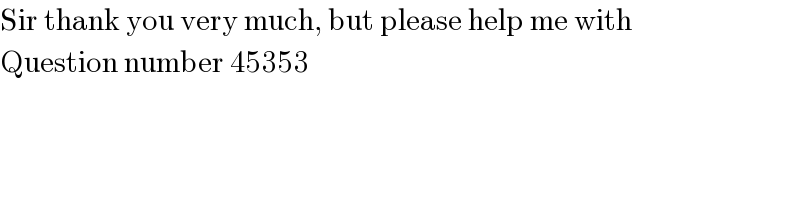Question and Answers Forum
Question Number 45585 by pieroo last updated on 14/Oct/18
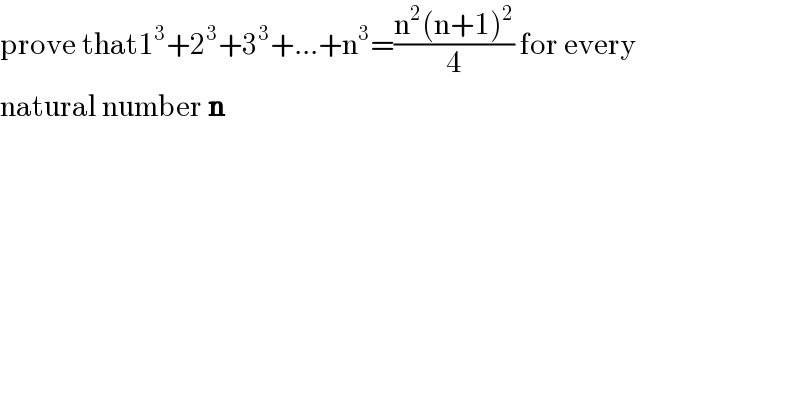
Commented by maxmathsup by imad last updated on 14/Oct/18
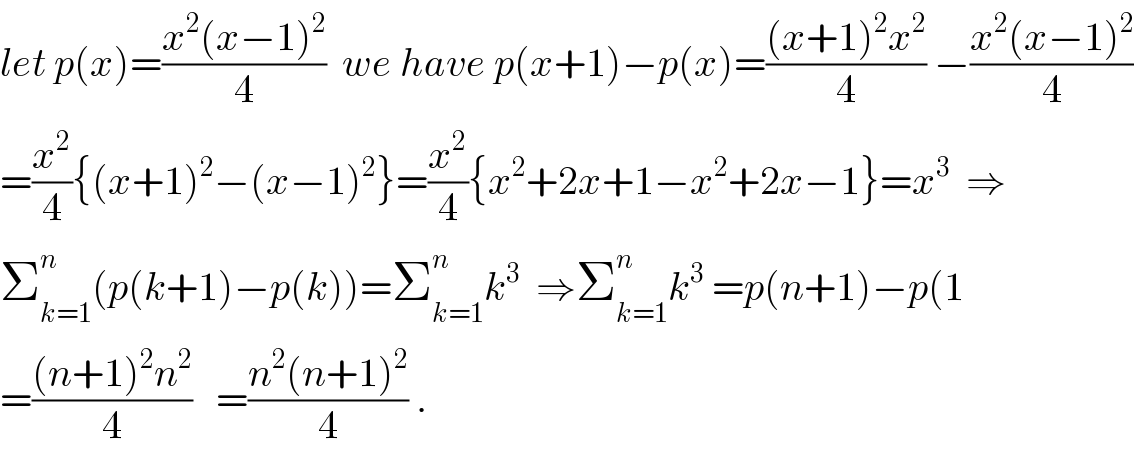
Commented by pieroo last updated on 14/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18
![another general method... S_r =1^r +2^r +3^r +...+n^r formuls is S_r =r∫S_(r−1) dn+nB_r now if we know s_1 =1+2+3+...+n we can find S_2 =1^2 +2^2 +3^2 +...+n^2 S_3 =1^3 +2^3 +3^3 +..+n^3 S_(40) =1^(40) +2^(40) +3^(40) +...+n^(40) now s_1 =((n(n+1))/2)=(n^2 /2)+(n/2) S_r =r∫S_(r−1) dn+nB_r so S_2 =2∫S_1 dn+nB_2 =2∫((n^2 /2)+(n/2))dn+nB_2 =2[(n^3 /6)+(n^2 /4)]+n×(1/6) B_2 =(1/6) (see table) =(n^3 /3)+(n^2 /2)+(n/6)=((2n^3 +3n^2 +n)/6) =((n(2n^2 +3n+1))/6)=(n/6)(2n^2 +2n+n+1) =((n(n+1)(2n+1))/6) using this we can find S_3 =3∫S_2 dn+nB_3 S_3 =3∫(n^3 /3)+(n^2 /2)+(n/6)+n×0 B_3 =0 =3((n^4 /(12))+(n^3 /6)+(n^2 /(12)))=(n^4 /4)+(n^3 /2)+(n^2 /4)=(n^2 /4)(n^2 +2n+1) =(n^2 /4)(n+1)^2 ={((n(n+1))/2)}^2 is the answer](Q45621.png)
Commented by pieroo last updated on 14/Oct/18

Commented by pieroo last updated on 14/Oct/18