
Question and Answers Forum
Question Number 45632 by maxmathsup by imad last updated on 14/Oct/18
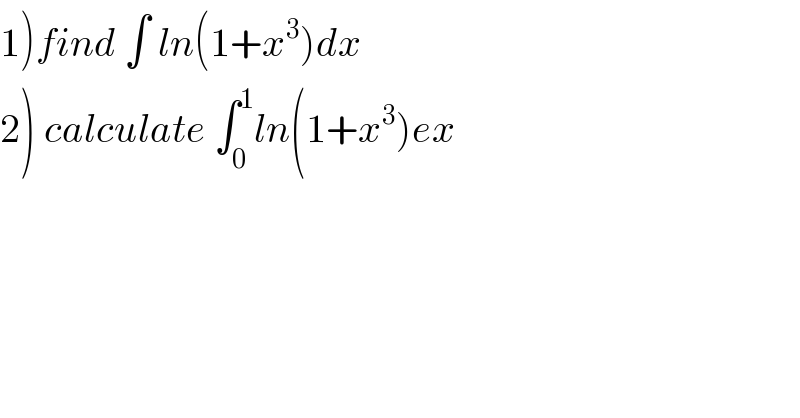
Commented by maxmathsup by imad last updated on 16/Oct/18

Commented by maxmathsup by imad last updated on 16/Oct/18
![∫_0 ^1 (dx/(1+x^3 )) =[xln(1+x^3 )−3x +ln((∣x+1∣)/(√(x^2 −x+1))) +(√3)arctan(((2x−1)/(√3)))]_0 ^1 =ln(2)−3 +ln(2) +(√3) arctan((1/(√3))) +(√3)arctan((1/(√3))) =2ln(2)−3 +2 (√3)(π/6) =2ln(2) +((π(√3))/3) −3 .](Q45767.png)
| ||
Question and Answers Forum | ||
Question Number 45632 by maxmathsup by imad last updated on 14/Oct/18 | ||
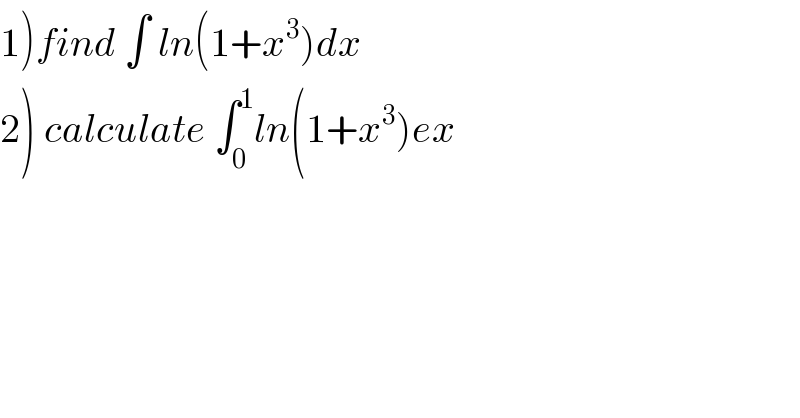 | ||
Commented by maxmathsup by imad last updated on 16/Oct/18 | ||
 | ||
Commented by maxmathsup by imad last updated on 16/Oct/18 | ||
![∫_0 ^1 (dx/(1+x^3 )) =[xln(1+x^3 )−3x +ln((∣x+1∣)/(√(x^2 −x+1))) +(√3)arctan(((2x−1)/(√3)))]_0 ^1 =ln(2)−3 +ln(2) +(√3) arctan((1/(√3))) +(√3)arctan((1/(√3))) =2ln(2)−3 +2 (√3)(π/6) =2ln(2) +((π(√3))/3) −3 .](Q45767.png) | ||