Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 45706 by Meritguide1234 last updated on 15/Oct/18

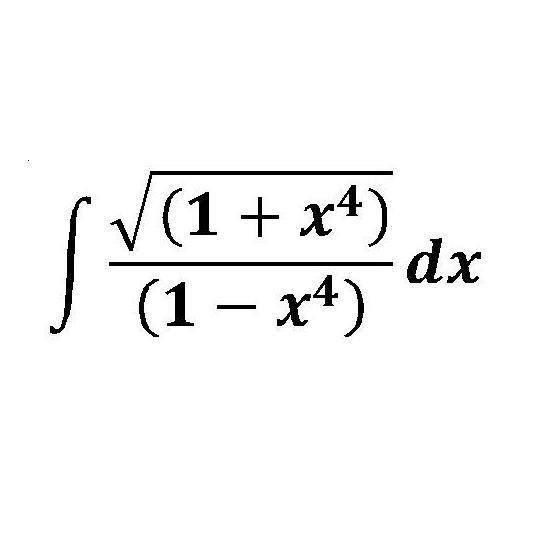
	Answered by tanmay.chaudhury50@gmail.com last updated on 17/Oct/18
	$trying to solve... ∫(((1+x^4 ))/((1−x^4 )(√(1+x^4 )) ))dx ∫((1+x^4 )/(x^2 ((1/x^2 )−x^2 )×x(√((1/x^2 )+x^2 )) ))dx ∫(((1/x^3 )+x)/(((1/x^2 )−x^2 )×{((1/x^2 )+x^2 )^2 }^(1/4) ))dx ∫((((1/x^3 )+x)dx)/(((1/x^2 )−x^2 )×{((1/x^2 )−x^2 )^2 +4}^(1/4) )) t=(1/x^2 )−x^2 (dt/dx)=((−2)/x^3 )−2x (dt/(−2))=((1/x^3 )+x)dx ∫(dt/(−2×t×(t^2 +4)^(1/4) )) ((−1)/2)∫((tdt)/(t^2 ×(t^2 +4)^(1/4) )) y^4 =t^2 +4 4y^3 ×(dy/dt)=2t ((−1)/2)∫((2y^3 dy)/((y^4 −4)×y)) =−1∫((y^2 dy)/((y^2 +1)(y^2 −1))) =((−1)/2)∫((y^2 +1+y^2 −1)/((y^2 +1)(y^2 −1)))dy ((−1)/2)[∫(dy/(y^2 −1))+∫(dy/(y^2 +1))] =((−1)/2)[{(1/2)∫(((y+1)−(y−1})/((y+1)(y−1)))+∫(dy/(y^2 +1))] ((−1)/2)[{(1/2)×∫(dy/(y−1))−(1/2)∫(dy/(y+1))+∫(dy/(y^2 +1)) dy] =((−1)/2)[(1/2)ln(((y−1)/(y+1)))+tan^(−1) y] =((−1)/2)[(1/2)ln{(((t^2 +4)^(1/4) −1)/((t^2 +4)^(1/4) +1))}+tan^(−1) (t^2 +4)^(1/4) ]+c =((−1)/2)[(1/2)ln∣(({((1/x^2 )−x^2 )^2 +4}^(1/4) −1)/({((1/x^2 )−x^2 )^2 +4}^(1/4) +2))∣+tan^(−1) {((1/x^2 )−x)^2 +4}^(1/4) +c$
	$t r y i n g t o s o l v e . . .$ $\int \frac{(1 + x^{4})}{(1 - x^{4}) \sqrt{1 + x^{4}}} d x$ $\int \frac{1 + x^{4}}{x^{2} (\frac{1}{x^{2}} - x^{2}) \times x \sqrt{\frac{1}{x^{2}} + x^{2}}} d x$ $\int \frac{\frac{1}{x^{3}} + x}{(\frac{1}{x^{2}} - x^{2}) \times {{(\frac{1}{x^{2}} + x^{2})}^{2}}^{\frac{1}{4}}} d x$ $\int \frac{(\frac{1}{x^{3}} + x) d x}{(\frac{1}{x^{2}} - x^{2}) \times {{(\frac{1}{x^{2}} - x^{2})}^{2} + 4}^{\frac{1}{4}}}$ $t = \frac{1}{x^{2}} - x^{2} \frac{d t}{d x} = \frac{- 2}{x^{3}} - 2 x \frac{d t}{- 2} = (\frac{1}{x^{3}} + x) d x$ $\int \frac{d t}{- 2 \times t \times {(t^{2} + 4)}^{\frac{1}{4}}}$ $\frac{- 1}{2} \int \frac{t d t}{t^{2} \times {(t^{2} + 4)}^{\frac{1}{4}}}$ $y^{4} = t^{2} + 4 4 y^{3} \times \frac{d y}{d t} = 2 t$ $\frac{- 1}{2} \int \frac{2 y^{3} d y}{(y^{4} - 4) \times y}$ $= - 1 \int \frac{y^{2} d y}{(y^{2} + 1) (y^{2} - 1)}$ $= \frac{- 1}{2} \int \frac{y^{2} + 1 + y^{2} - 1}{(y^{2} + 1) (y^{2} - 1)} d y$ $\frac{- 1}{2} [\int \frac{d y}{y^{2} - 1} + \int \frac{d y}{y^{2} + 1}]$ $= \frac{- 1}{2} [{\frac{1}{2} \int \frac{(y + 1) - (y - 1}}{(y + 1) (y - 1)} + \int \frac{d y}{y^{2} + 1}]$ $\frac{- 1}{2} [{\frac{1}{2} \times \int \frac{d y}{y - 1} - \frac{1}{2} \int \frac{d y}{y + 1} + \int \frac{d y}{y^{2} + 1} d y]$ $= \frac{- 1}{2} [\frac{1}{2} l n (\frac{y - 1}{y + 1}) + {t a n}^{- 1} y]$ $= \frac{- 1}{2} [\frac{1}{2} l n {\frac{{(t^{2} + 4)}^{\frac{1}{4}} - 1}{{(t^{2} + 4)}^{\frac{1}{4}} + 1}} + {t a n}^{- 1} {(t^{2} + 4)}^{\frac{1}{4}}] + c$ $= \frac{- 1}{2} [\frac{1}{2} l n ∣ \frac{{{(\frac{1}{x^{2}} - x^{2})}^{2} + 4}^{\frac{1}{4}} - 1}{{{(\frac{1}{x^{2}} - x^{2})}^{2} + 4}^{\frac{1}{4}} + 2} ∣ + {t a n}^{- 1} {{(\frac{1}{x^{2}} - x)}^{2} + 4}^{\frac{1}{4}} + c$
	Commented by Meritguide1234 last updated on 18/Oct/18

	$n i c e$
	Commented by tanmay.chaudhury50@gmail.com last updated on 18/Oct/18

	$t h a n k y o u s i r . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum