Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 45957 by maxmathsup by imad last updated on 19/Oct/18

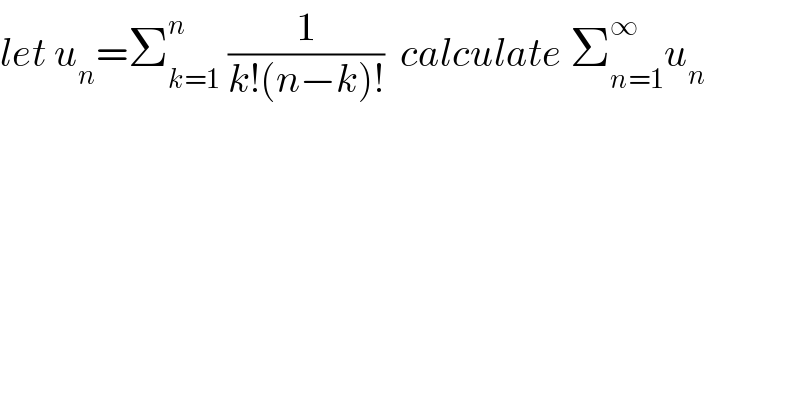
let u_n =Σ_(k=1) ^n (1/(k!(n−k)!)) calculate Σ_(n=1) ^∞ u_n

$${let}\:{u}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}!\left({n}−{k}\right)!}\:\:{calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} {u}_{{n}} \\ $$

Commented by maxmathsup by imad last updated on 20/Oct/18

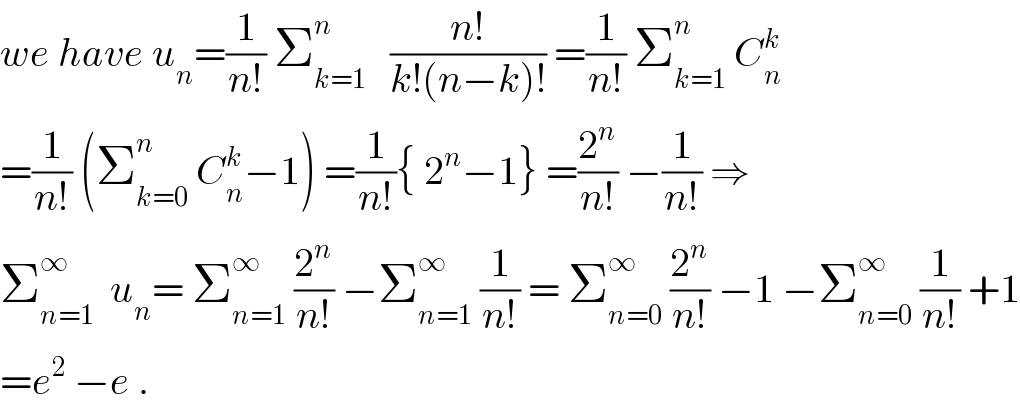
we have u_n =(1/(n!)) Σ_(k=1) ^n ((n!)/(k!(n−k)!)) =(1/(n!)) Σ_(k=1) ^n C_n ^k =(1/(n!)) (Σ_(k=0) ^n C_n ^k −1) =(1/(n!)){ 2^n −1} =(2^n /(n!)) −(1/(n!)) ⇒ Σ_(n=1) ^∞ u_n = Σ_(n=1) ^∞ (2^n /(n!)) −Σ_(n=1) ^∞ (1/(n!)) = Σ_(n=0) ^∞ (2^n /(n!)) −1 −Σ_(n=0) ^∞ (1/(n!)) +1 =e^2 −e .

$${we}\:{have}\:{u}_{{n}} =\frac{\mathrm{1}}{{n}!}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{{n}!}{{k}!\left({n}−{k}\right)!}\:=\frac{\mathrm{1}}{{n}!}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \\ $$$$=\frac{\mathrm{1}}{{n}!}\:\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} −\mathrm{1}\right)\:=\frac{\mathrm{1}}{{n}!}\left\{\:\mathrm{2}^{{n}} −\mathrm{1}\right\}\:=\frac{\mathrm{2}^{{n}} }{{n}!}\:−\frac{\mathrm{1}}{{n}!}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:{u}_{{n}} =\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}^{{n}} }{{n}!}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{{n}} }{{n}!}\:−\mathrm{1}\:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\:+\mathrm{1} \\ $$$$={e}^{\mathrm{2}} \:−{e}\:. \\ $$

Answered by Smail last updated on 19/Oct/18

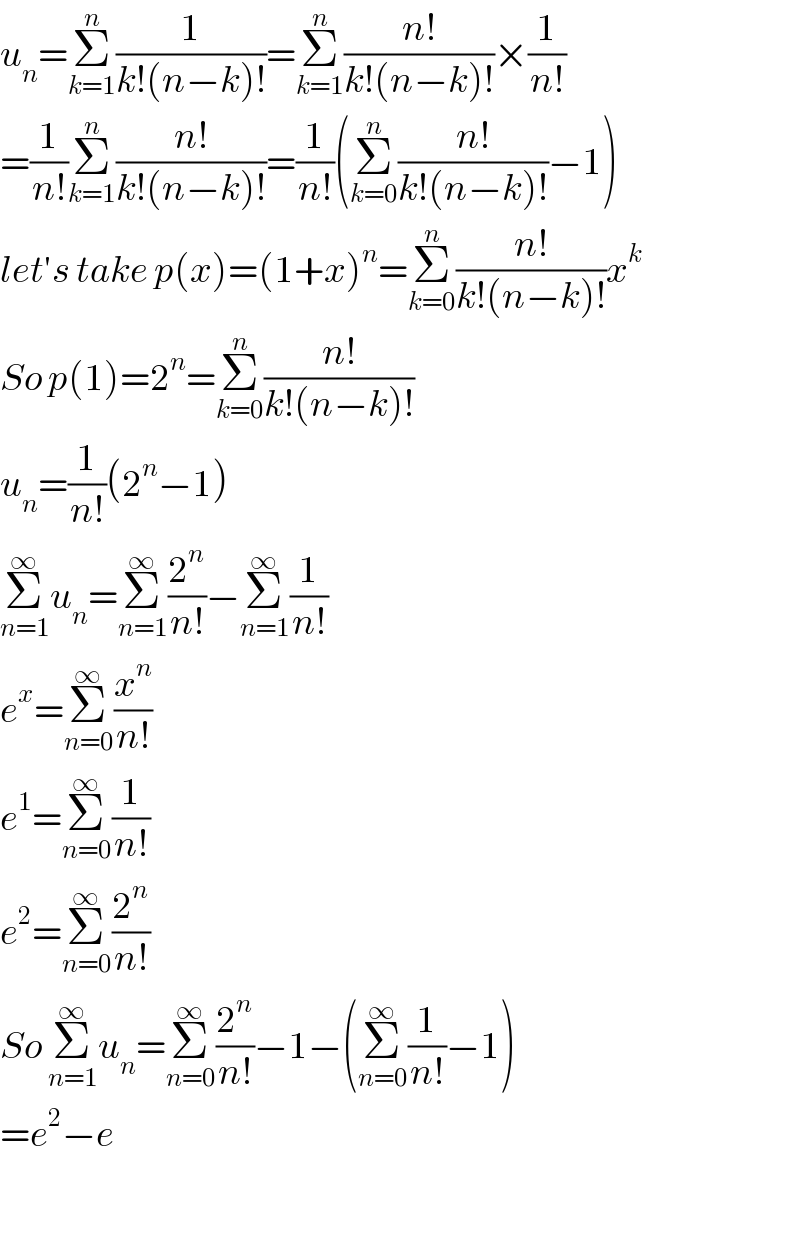
u_n =Σ_(k=1) ^n (1/(k!(n−k)!))=Σ_(k=1) ^n ((n!)/(k!(n−k)!))×(1/(n!)) =(1/(n!))Σ_(k=1) ^n ((n!)/(k!(n−k)!))=(1/(n!))(Σ_(k=0) ^n ((n!)/(k!(n−k)!))−1) let′s take p(x)=(1+x)^n =Σ_(k=0) ^n ((n!)/(k!(n−k)!))x^k So p(1)=2^n =Σ_(k=0) ^n ((n!)/(k!(n−k)!)) u_n =(1/(n!))(2^n −1) Σ_(n=1) ^∞ u_n =Σ_(n=1) ^∞ (2^n /(n!))−Σ_(n=1) ^∞ (1/(n!)) e^x =Σ_(n=0) ^∞ (x^n /(n!)) e^1 =Σ_(n=0) ^∞ (1/(n!)) e^2 =Σ_(n=0) ^∞ (2^n /(n!)) So Σ_(n=1) ^∞ u_n =Σ_(n=0) ^∞ (2^n /(n!))−1−(Σ_(n=0) ^∞ (1/(n!))−1) =e^2 −e

$${u}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}!\left({n}−{k}\right)!}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{n}!}{{k}!\left({n}−{k}\right)!}×\frac{\mathrm{1}}{{n}!} \\ $$$$=\frac{\mathrm{1}}{{n}!}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{n}!}{{k}!\left({n}−{k}\right)!}=\frac{\mathrm{1}}{{n}!}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{{k}!\left({n}−{k}\right)!}−\mathrm{1}\right) \\ $$$${let}'{s}\:{take}\:{p}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{{k}!\left({n}−{k}\right)!}{x}^{{k}} \\ $$$${So}\:{p}\left(\mathrm{1}\right)=\mathrm{2}^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{{k}!\left({n}−{k}\right)!} \\ $$$${u}_{{n}} =\frac{\mathrm{1}}{{n}!}\left(\mathrm{2}^{{n}} −\mathrm{1}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{n}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{{n}!}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$${e}^{\mathrm{1}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$${e}^{\mathrm{2}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{{n}!} \\ $$$${So}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{n}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{{n}!}−\mathrm{1}−\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}−\mathrm{1}\right) \\ $$$$={e}^{\mathrm{2}} −{e} \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 20/Oct/18

correct answer thanks...

$${correct}\:{answer}\:{thanks}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com