Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 45963 by maxmathsup by imad last updated on 19/Oct/18

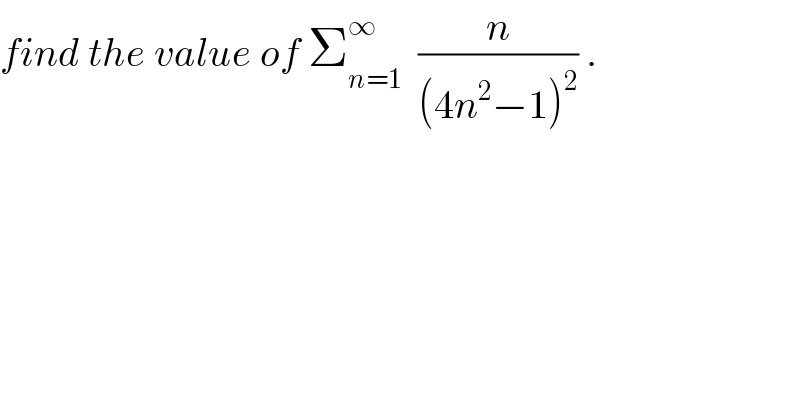
find the value of Σ_(n=1) ^∞ (n/((4n^2 −1)^2 )) .

$${find}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{n}}{\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:. \\ $$

Commented by maxmathsup by imad last updated on 23/Oct/18

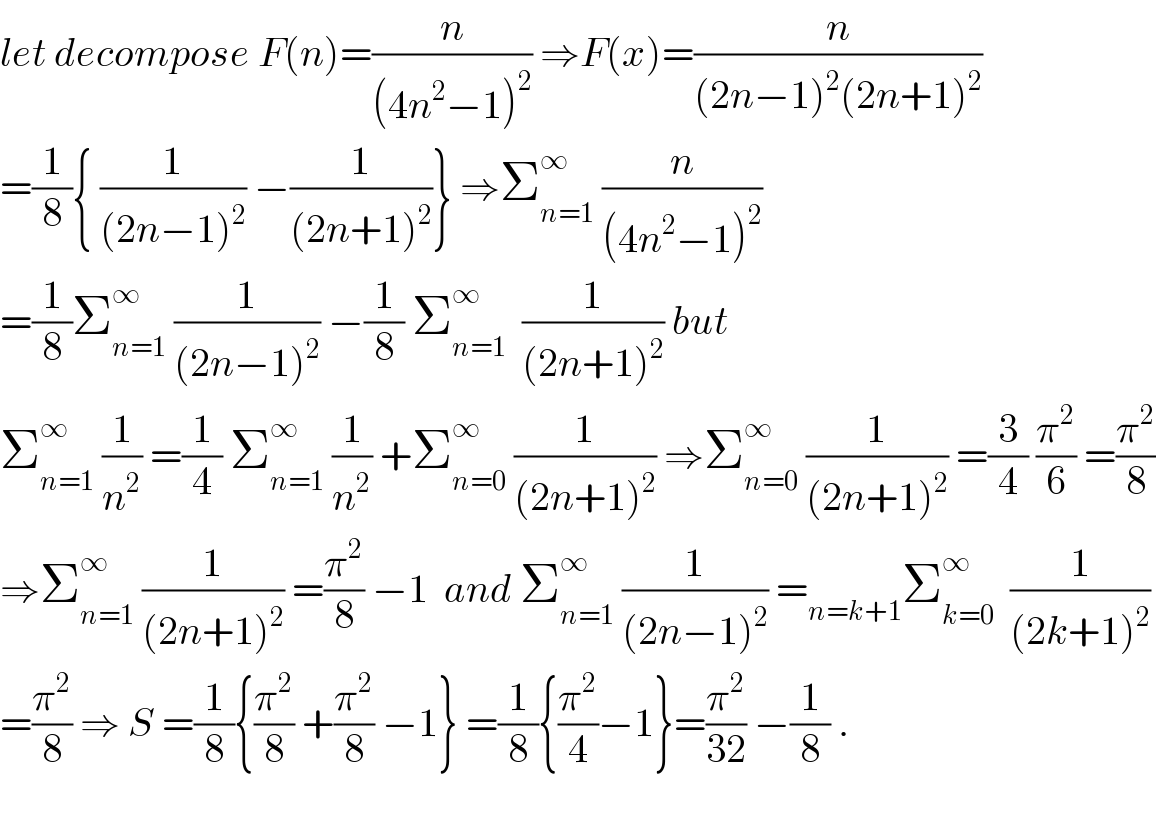
let decompose F(n)=(n/((4n^2 −1)^2 )) ⇒F(x)=(n/((2n−1)^2 (2n+1)^2 )) =(1/8){ (1/((2n−1)^2 )) −(1/((2n+1)^2 ))} ⇒Σ_(n=1) ^∞ (n/((4n^2 −1)^2 )) =(1/8)Σ_(n=1) ^∞ (1/((2n−1)^2 )) −(1/8) Σ_(n=1) ^∞ (1/((2n+1)^2 )) but Σ_(n=1) ^∞ (1/n^2 ) =(1/4) Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(3/4) (π^2 /6) =(π^2 /8) ⇒Σ_(n=1) ^∞ (1/((2n+1)^2 )) =(π^2 /8) −1 and Σ_(n=1) ^∞ (1/((2n−1)^2 )) =_(n=k+1) Σ_(k=0) ^∞ (1/((2k+1)^2 )) =(π^2 /8) ⇒ S =(1/8){(π^2 /8) +(π^2 /8) −1} =(1/8){(π^2 /4)−1}=(π^2 /(32)) −(1/8) .

$${let}\:{decompose}\:{F}\left({n}\right)=\frac{{n}}{\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{F}\left({x}\right)=\frac{{n}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right\}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{n}}{\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{8}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:{but} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{3}}{\mathrm{4}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\mathrm{1}\:\:{and}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:=_{{n}={k}+\mathrm{1}} \sum_{{k}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow\:{S}\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:+\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\mathrm{1}\right\}\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}\right\}=\frac{\pi^{\mathrm{2}} }{\mathrm{32}}\:−\frac{\mathrm{1}}{\mathrm{8}}\:. \\ $$$$ \\ $$

Answered by Smail last updated on 22/Oct/18

A=Σ_(n=1) ^∞ (n/((4n^2 −1)^2 ))=Σ_(n=1) ^∞ (n/((2n−1)^2 (2n+1)^2 )) (n/((2n−1)^2 (2n+1)^2 ))=(1/8)((1/((2n−1)^2 )) −(1/((2n+1)^2 )) A=(1/8)Σ_(n=1) ^∞ (1/((2n−1)^2 ))−(1/8)Σ_(n=1) ^∞ (1/((2n+1)^2 )) =(1/8)[Σ_(n=1) ^∞ (1/((2n−1)^2 ))+Σ_(n=1) ^∞ (1/((2n)^2 ))−(Σ_(n=1) ^∞ (1/((2n+1)^2 ))+Σ_(n=1) ^∞ (1/((2n)^2 )))] =(1/8)[Σ_(n=1) ^∞ (1/n^2 )−Σ_(n=2) ^∞ (1/n^2 )] =(1/8)(1)=(1/8)

$${A}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{{n}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right. \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} }−\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} }\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com