Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 4597 by FilupSmith last updated on 10/Feb/16

a_n =(√a_(n−1) ) a_1 =c Solve: S = lim_(n→∞) a_n

$${a}_{{n}} =\sqrt{{a}_{{n}−\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} ={c} \\ $$$$ \\ $$$$\mathrm{Solve}: \\ $$$${S}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \\ $$

Commented by FilupSmith last updated on 10/Feb/16

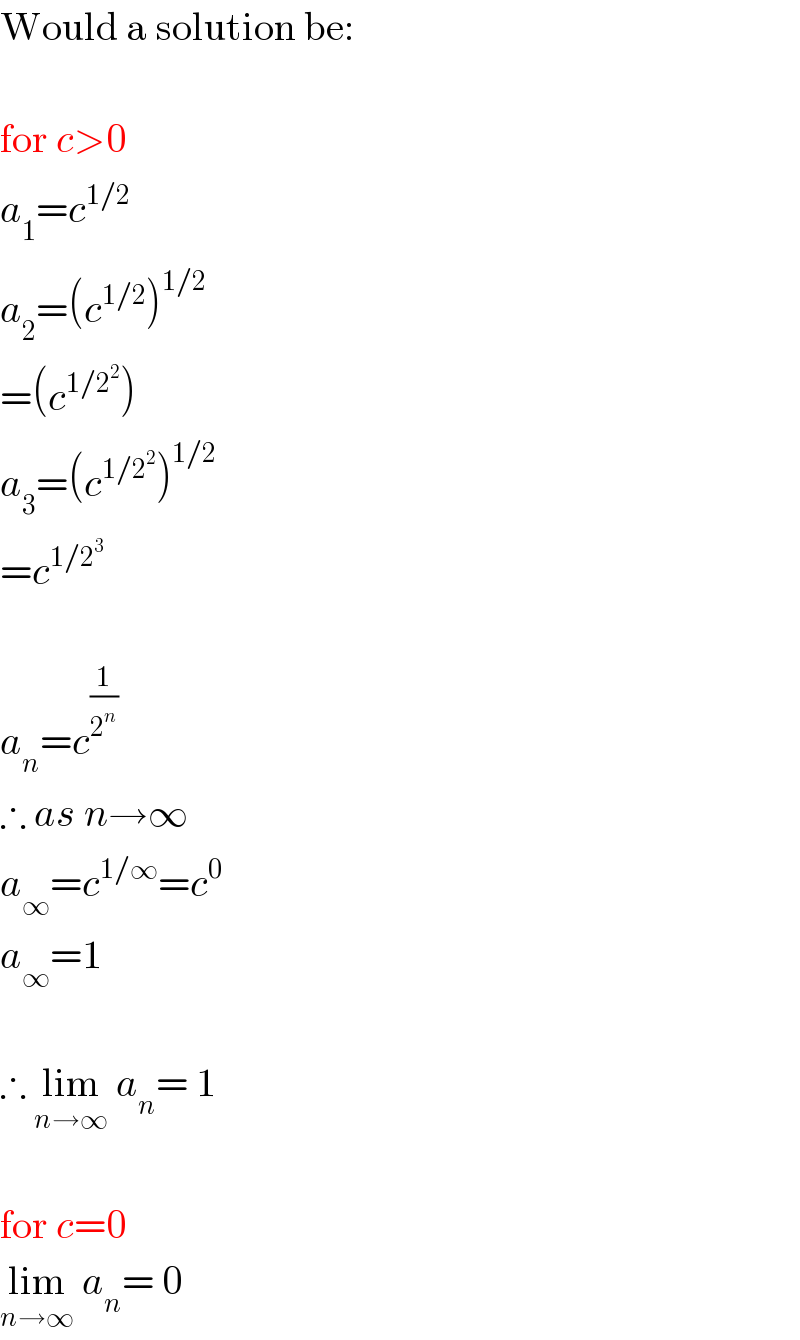
Would a solution be: for c>0 a_1 =c^(1/2) a_2 =(c^(1/2) )^(1/2) =(c^(1/2^2 ) ) a_3 =(c^(1/2^2 ) )^(1/2) =c^(1/2^3 ) a_n =c^(1/2^n ) ∴ as n→∞ a_∞ =c^(1/∞) =c^0 a_∞ =1 ∴ lim_(n→∞) a_n = 1 for c=0 lim_(n→∞) a_n = 0

$$\mathrm{Would}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{be}: \\ $$$$ \\ $$$$\mathrm{for}\:{c}>\mathrm{0} \\ $$$${a}_{\mathrm{1}} ={c}^{\mathrm{1}/\mathrm{2}} \\ $$$${a}_{\mathrm{2}} =\left({c}^{\mathrm{1}/\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} \\ $$$$=\left({c}^{\mathrm{1}/\mathrm{2}^{\mathrm{2}} } \right) \\ $$$${a}_{\mathrm{3}} =\left({c}^{\mathrm{1}/\mathrm{2}^{\mathrm{2}} } \right)^{\mathrm{1}/\mathrm{2}} \\ $$$$={c}^{\mathrm{1}/\mathrm{2}^{\mathrm{3}} } \\ $$$$ \\ $$$${a}_{{n}} ={c}^{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }} \\ $$$$\therefore\:{as}\:{n}\rightarrow\infty \\ $$$${a}_{\infty} ={c}^{\mathrm{1}/\infty} ={c}^{\mathrm{0}} \\ $$$${a}_{\infty} =\mathrm{1} \\ $$$$ \\ $$$$\therefore\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} =\:\mathrm{1} \\ $$$$ \\ $$$$\mathrm{for}\:{c}=\mathrm{0} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} =\:\mathrm{0} \\ $$

Commented by Yozzii last updated on 10/Feb/16

This appears to be legitimate for if c=0, a_n =0^(1/2^(n−1) ) =0 ∀n∈N⇒lim_(n→+∞) a_n =lim_(n→+∞) 0=0. The term a_∞ does not exist by the way. It′s better to say ′ as n→∞, 2^(n−1) →∞ ⇒(1/2^(n−1) )→0⇒c^(1/2^(n−1) ) →c^0 =1⇒a_n →1.′ To further convince your audience of the obvious pattern that a_n =c^(1/2^(n−1) ) , given that a_1 =c>0 and a_(n+1) =(√a_n ), use induction on n. (I saw that you wrote a_1 =c^(1/2) when the information gave a_1 =c. It′s really a_2 =(√a_1 )=c^(1/2) ⇒ a_3 =(√a_2 )=c^(1/2^2 ) ⇒a_4 =(√a_3 )=c^(1/2^3 ) ⇒...⇒a_n =c^(1/2^(n−1) ) (n∈N).)

$${This}\:{appears}\:{to}\:{be}\:{legitimate}\:{for}\:{if} \\ $$$${c}=\mathrm{0},\:{a}_{{n}} =\mathrm{0}^{\mathrm{1}/\mathrm{2}^{{n}−\mathrm{1}} } =\mathrm{0}\:\:\forall{n}\in\mathbb{N}\Rightarrow\underset{{n}\rightarrow+\infty} {\mathrm{lim}}{a}_{{n}} =\underset{{n}\rightarrow+\infty} {\mathrm{lim}0}=\mathrm{0}. \\ $$$${The}\:{term}\:{a}_{\infty} \:{does}\:{not}\:{exist}\:{by}\:{the}\:{way}. \\ $$$${It}'{s}\:{better}\:{to}\:{say}\:'\:{as}\:{n}\rightarrow\infty,\:\mathrm{2}^{{n}−\mathrm{1}} \rightarrow\infty \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\rightarrow\mathrm{0}\Rightarrow{c}^{\mathrm{1}/\mathrm{2}^{{n}−\mathrm{1}} } \rightarrow{c}^{\mathrm{0}} =\mathrm{1}\Rightarrow{a}_{{n}} \rightarrow\mathrm{1}.' \\ $$$${To}\:{further}\:{convince}\:{your}\:{audience} \\ $$$${of}\:{the}\:{obvious}\:{pattern}\:{that}\:{a}_{{n}} ={c}^{\mathrm{1}/\mathrm{2}^{{n}−\mathrm{1}} } , \\ $$$${given}\:{that}\:{a}_{\mathrm{1}} ={c}>\mathrm{0}\:{and}\:{a}_{{n}+\mathrm{1}} =\sqrt{{a}_{{n}} }, \\ $$$${use}\:{induction}\:{on}\:{n}.\:\left({I}\:{saw}\:{that}\:{you}\right. \\ $$$${wrote}\:{a}_{\mathrm{1}} ={c}^{\mathrm{1}/\mathrm{2}} \:{when}\:{the}\:{information} \\ $$$${gave}\:{a}_{\mathrm{1}} ={c}.\:{It}'{s}\:{really}\:{a}_{\mathrm{2}} =\sqrt{{a}_{\mathrm{1}} }={c}^{\mathrm{1}/\mathrm{2}} \Rightarrow \\ $$$$\left.{a}_{\mathrm{3}} =\sqrt{{a}_{\mathrm{2}} }={c}^{\mathrm{1}/\mathrm{2}^{\mathrm{2}} } \Rightarrow{a}_{\mathrm{4}} =\sqrt{{a}_{\mathrm{3}} }={c}^{\mathrm{1}/\mathrm{2}^{\mathrm{3}} } \Rightarrow...\Rightarrow{a}_{{n}} ={c}^{\mathrm{1}/\mathrm{2}^{{n}−\mathrm{1}} } \:\:\left({n}\in\mathbb{N}\right).\right) \\ $$$$ \\ $$

Commented by FilupSmith last updated on 11/Feb/16

Thanks. I do not know induction. I have been meaning to learn but i can′t find an easy to understand explanation

$$\mathrm{Thanks}.\:\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{know}\:\mathrm{induction}.\:\mathrm{I}\:\mathrm{have} \\ $$$$\mathrm{been}\:\mathrm{meaning}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{but}\:\mathrm{i}\:\mathrm{can}'\mathrm{t} \\ $$$$\mathrm{find}\:\mathrm{an}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{explanation} \\ $$

Commented by Yozzii last updated on 11/Feb/16

The underlying principle of mathematical induction is the idea that you can obtain an integer k+1 if you know what k is,being an integer. So, given an integer k you can get the next integer by adding 1 to k⇒k+1. So, since you know what your initial integer is, e.g 1, you can find any integer greater than (or less than) 1 if you continue on from 1 to 2 ,then 2 to 3 ,then 3 to 4, ...., then k to k+1,then....to infinity. You can assign a mathematical idea P that depends on n to use induction to show that P(n) is true for all integers n since from, say P(1), you can deduce P(k),P(k+1),P(k+2)....

$${The}\:{underlying}\:{principle}\:{of}\: \\ $$$${mathematical}\:{induction}\:{is}\: \\ $$$${the}\:{idea}\:{that}\:{you}\:{can}\:{obtain}\:{an}\:{integer} \\ $$$${k}+\mathrm{1}\:{if}\:{you}\:{know}\:{what}\:{k}\:{is},{being}\:{an} \\ $$$${integer}.\:{So},\:{given}\:{an}\:{integer}\:{k}\: \\ $$$${you}\:{can}\:{get}\:{the}\:{next}\:{integer}\:{by}\:{adding} \\ $$$$\mathrm{1}\:{to}\:{k}\Rightarrow{k}+\mathrm{1}.\:{So},\:{since}\:{you}\:{know}\: \\ $$$${what}\:{your}\:{initial}\:{integer}\:{is},\:{e}.{g}\:\mathrm{1}, \\ $$$${you}\:{can}\:{find}\:{any}\:{integer}\:{greater}\:{than} \\ $$$$\left({or}\:{less}\:{than}\right)\:\mathrm{1}\:{if}\:{you}\:{continue}\:{on} \\ $$$${from}\:\mathrm{1}\:{to}\:\mathrm{2}\:,{then}\:\mathrm{2}\:{to}\:\mathrm{3}\:,{then}\:\mathrm{3}\:{to}\:\mathrm{4}, \\ $$$$....,\:{then}\:{k}\:{to}\:{k}+\mathrm{1},{then}....{to}\:{infinity}. \\ $$$${You}\:{can}\:{assign}\:{a}\:{mathematical} \\ $$$${idea}\:{P}\:\:{that}\:{depends}\:{on}\:{n}\:{to}\:{use}\: \\ $$$${induction}\:{to}\:{show}\:{that}\:{P}\left({n}\right)\:{is}\:{true} \\ $$$${for}\:{all}\:{integers}\:{n}\:{since}\:{from},\:{say}\:{P}\left(\mathrm{1}\right), \\ $$$${you}\:{can}\:{deduce}\:{P}\left({k}\right),{P}\left({k}+\mathrm{1}\right),{P}\left({k}+\mathrm{2}\right).... \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com