
Question Number 4614 by love math last updated on 14/Feb/16

$$\sqrt{{x}^{{log}_{\mathrm{2}} \sqrt{{x}}} }>\mathrm{2} \\ $$
Commented byYozzii last updated on 14/Feb/16
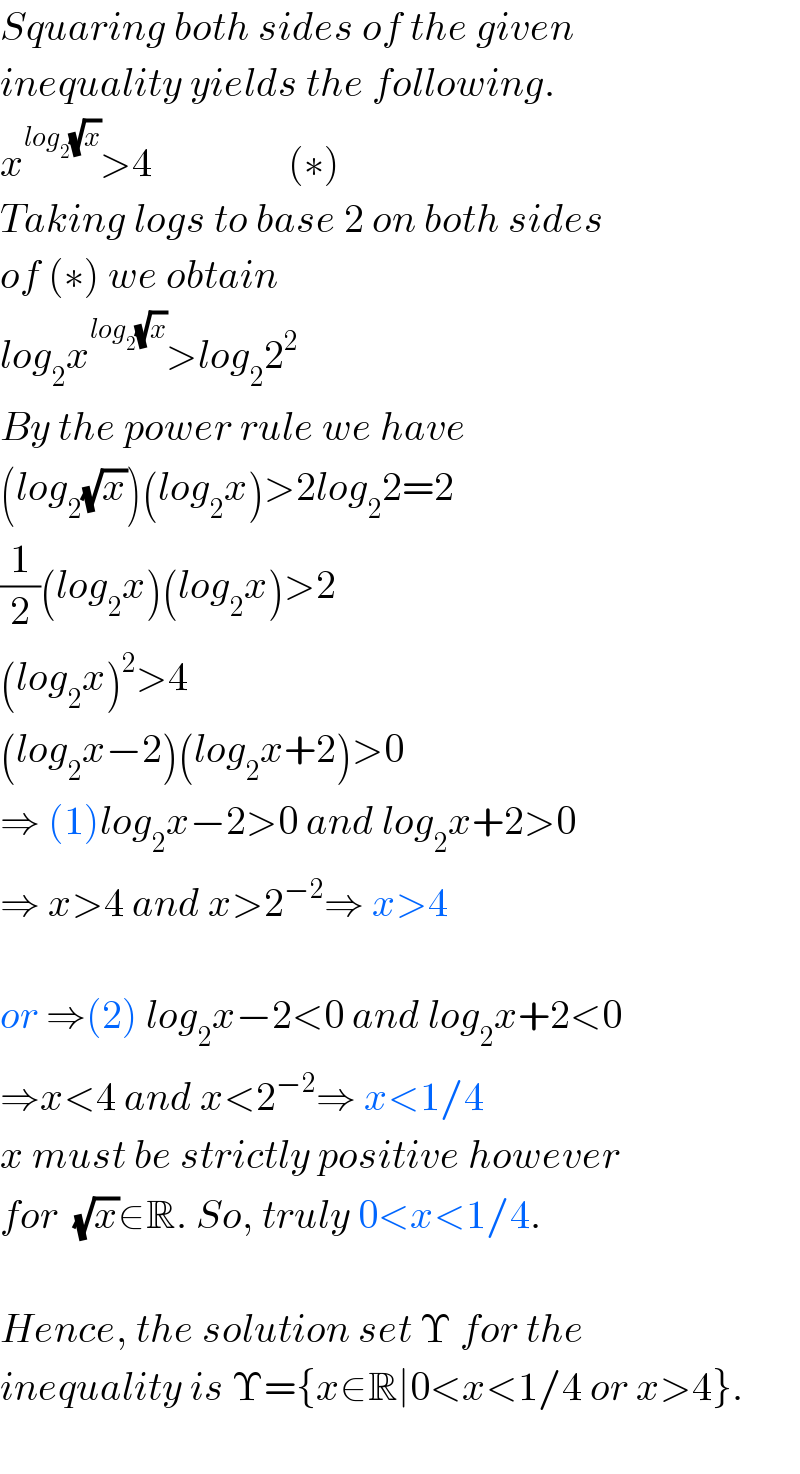
$${Squaring}\:{both}\:{sides}\:{of}\:{the}\:{given}\: \\ $$ $${inequality}\:{yields}\:{the}\:{following}. \\ $$ $${x}^{{log}_{\mathrm{2}} \sqrt{{x}}} >\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\ast\right) \\ $$ $${Taking}\:{logs}\:{to}\:{base}\:\mathrm{2}\:{on}\:{both}\:{sides} \\ $$ $${of}\:\left(\ast\right)\:{we}\:{obtain}\: \\ $$ $${log}_{\mathrm{2}} {x}^{{log}_{\mathrm{2}} \sqrt{{x}}} >{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}} \\ $$ $${By}\:{the}\:{power}\:{rule}\:{we}\:{have}\: \\ $$ $$\left({log}_{\mathrm{2}} \sqrt{{x}}\right)\left({log}_{\mathrm{2}} {x}\right)>\mathrm{2}{log}_{\mathrm{2}} \mathrm{2}=\mathrm{2} \\ $$ $$\frac{\mathrm{1}}{\mathrm{2}}\left({log}_{\mathrm{2}} {x}\right)\left({log}_{\mathrm{2}} {x}\right)>\mathrm{2} \\ $$ $$\left({log}_{\mathrm{2}} {x}\right)^{\mathrm{2}} >\mathrm{4} \\ $$ $$\left({log}_{\mathrm{2}} {x}−\mathrm{2}\right)\left({log}_{\mathrm{2}} {x}+\mathrm{2}\right)>\mathrm{0} \\ $$ $$\Rightarrow\:\left(\mathrm{1}\right){log}_{\mathrm{2}} {x}−\mathrm{2}>\mathrm{0}\:{and}\:{log}_{\mathrm{2}} {x}+\mathrm{2}>\mathrm{0} \\ $$ $$\Rightarrow\:{x}>\mathrm{4}\:{and}\:{x}>\mathrm{2}^{−\mathrm{2}} \Rightarrow\:{x}>\mathrm{4} \\ $$ $$ \\ $$ $${or}\:\Rightarrow\left(\mathrm{2}\right)\:{log}_{\mathrm{2}} {x}−\mathrm{2}<\mathrm{0}\:{and}\:{log}_{\mathrm{2}} {x}+\mathrm{2}<\mathrm{0} \\ $$ $$\Rightarrow{x}<\mathrm{4}\:{and}\:{x}<\mathrm{2}^{−\mathrm{2}} \Rightarrow\:{x}<\mathrm{1}/\mathrm{4} \\ $$ $${x}\:{must}\:{be}\:{strictly}\:{positive}\:{however} \\ $$ $${for}\:\:\sqrt{{x}}\in\mathbb{R}.\:{So},\:{truly}\:\mathrm{0}<{x}<\mathrm{1}/\mathrm{4}. \\ $$ $$ \\ $$ $${Hence},\:{the}\:{solution}\:{set}\:\Upsilon\:{for}\:{the}\: \\ $$ $${inequality}\:{is}\:\Upsilon=\left\{{x}\in\mathbb{R}\mid\mathrm{0}<{x}<\mathrm{1}/\mathrm{4}\:{or}\:{x}>\mathrm{4}\right\}. \\ $$ $$ \\ $$
