Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 4668 by FilupSmith last updated on 20/Feb/16

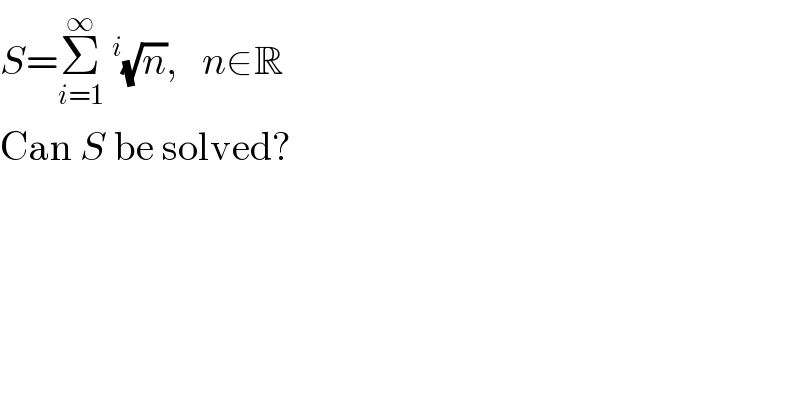
S=Σ_(i=1) ^∞ ^i (√n), n∈R Can S be solved?

$${S}=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\:^{{i}} \sqrt{{n}},\:\:\:{n}\in\mathbb{R} \\ $$$$\mathrm{Can}\:{S}\:\mathrm{be}\:\mathrm{solved}? \\ $$

Answered by Yozzii last updated on 20/Feb/16

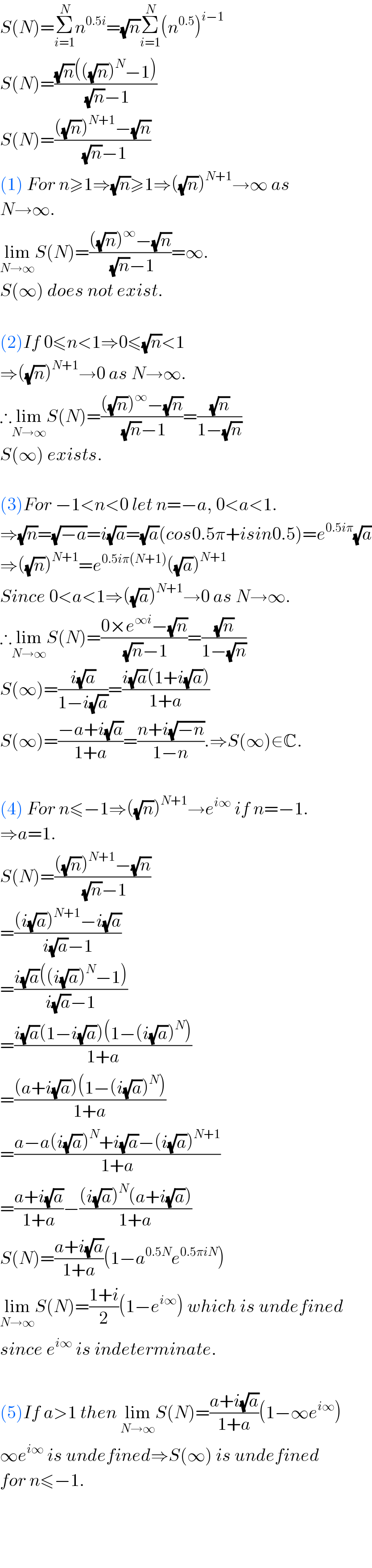
S(N)=Σ_(i=1) ^N n^(0.5i) =(√n)Σ_(i=1) ^N (n^(0.5) )^(i−1) S(N)=(((√n)(((√n))^N −1))/((√n)−1)) S(N)=((((√n))^(N+1) −(√n))/((√n)−1)) (1) For n≥1⇒(√n)≥1⇒((√n))^(N+1) →∞ as N→∞. lim_(N→∞) S(N)=((((√n))^∞ −(√n))/((√n)−1))=∞. S(∞) does not exist. (2)If 0≤n<1⇒0≤(√n)<1 ⇒((√n))^(N+1) →0 as N→∞. ∴lim_(N→∞) S(N)=((((√n))^∞ −(√n))/((√n)−1))=((√n)/(1−(√n))) S(∞) exists. (3)For −1<n<0 let n=−a, 0<a<1. ⇒(√n)=(√(−a))=i(√a)=(√a)(cos0.5π+isin0.5)=e^(0.5iπ) (√a) ⇒((√n))^(N+1) =e^(0.5iπ(N+1)) ((√a))^(N+1) Since 0<a<1⇒((√a))^(N+1) →0 as N→∞. ∴lim_(N→∞) S(N)=((0×e^(∞i) −(√n))/((√n)−1))=((√n)/(1−(√n))) S(∞)=((i(√a))/(1−i(√a)))=((i(√a)(1+i(√a)))/(1+a)) S(∞)=((−a+i(√a))/(1+a))=((n+i(√(−n)))/(1−n)).⇒S(∞)∈C. (4) For n≤−1⇒((√n))^(N+1) →e^(i∞) if n=−1. ⇒a=1. S(N)=((((√n))^(N+1) −(√n))/((√n)−1)) =(((i(√a))^(N+1) −i(√a))/(i(√a)−1)) =((i(√a)((i(√a))^N −1))/(i(√a)−1)) =((i(√a)(1−i(√a))(1−(i(√a))^N ))/(1+a)) =(((a+i(√a))(1−(i(√a))^N ))/(1+a)) =((a−a(i(√a))^N +i(√a)−(i(√a))^(N+1) )/(1+a)) =((a+i(√a))/(1+a))−(((i(√a))^N (a+i(√a)))/(1+a)) S(N)=((a+i(√a))/(1+a))(1−a^(0.5N) e^(0.5πiN) ) lim_(N→∞) S(N)=((1+i)/2)(1−e^(i∞) ) which is undefined since e^(i∞) is indeterminate. (5)If a>1 then lim_(N→∞) S(N)=((a+i(√a))/(1+a))(1−∞e^(i∞) ) ∞e^(i∞) is undefined⇒S(∞) is undefined for n≤−1.

$${S}\left({N}\right)=\underset{{i}=\mathrm{1}} {\overset{{N}} {\sum}}{n}^{\mathrm{0}.\mathrm{5}{i}} =\sqrt{{n}}\underset{{i}=\mathrm{1}} {\overset{{N}} {\sum}}\left({n}^{\mathrm{0}.\mathrm{5}} \right)^{{i}−\mathrm{1}} \\ $$$${S}\left({N}\right)=\frac{\sqrt{{n}}\left(\left(\sqrt{{n}}\right)^{{N}} −\mathrm{1}\right)}{\sqrt{{n}}−\mathrm{1}} \\ $$$${S}\left({N}\right)=\frac{\left(\sqrt{{n}}\right)^{{N}+\mathrm{1}} −\sqrt{{n}}}{\sqrt{{n}}−\mathrm{1}} \\ $$$$\left(\mathrm{1}\right)\:{For}\:{n}\geqslant\mathrm{1}\Rightarrow\sqrt{{n}}\geqslant\mathrm{1}\Rightarrow\left(\sqrt{{n}}\right)^{{N}+\mathrm{1}} \rightarrow\infty\:{as}\: \\ $$$${N}\rightarrow\infty. \\ $$$$\underset{{N}\rightarrow\infty} {\mathrm{lim}}{S}\left({N}\right)=\frac{\left(\sqrt{{n}}\right)^{\infty} −\sqrt{{n}}}{\sqrt{{n}}−\mathrm{1}}=\infty. \\ $$$${S}\left(\infty\right)\:{does}\:{not}\:{exist}.\: \\ $$$$ \\ $$$$\left(\mathrm{2}\right){If}\:\mathrm{0}\leqslant{n}<\mathrm{1}\Rightarrow\mathrm{0}\leqslant\sqrt{{n}}<\mathrm{1} \\ $$$$\Rightarrow\left(\sqrt{{n}}\right)^{{N}+\mathrm{1}} \rightarrow\mathrm{0}\:{as}\:{N}\rightarrow\infty. \\ $$$$\therefore\underset{{N}\rightarrow\infty} {\mathrm{lim}}{S}\left({N}\right)=\frac{\left(\sqrt{{n}}\right)^{\infty} −\sqrt{{n}}}{\sqrt{{n}}−\mathrm{1}}=\frac{\sqrt{{n}}}{\mathrm{1}−\sqrt{{n}}} \\ $$$${S}\left(\infty\right)\:{exists}. \\ $$$$ \\ $$$$\left(\mathrm{3}\right){For}\:−\mathrm{1}<{n}<\mathrm{0}\:{let}\:{n}=−{a},\:\mathrm{0}<{a}<\mathrm{1}. \\ $$$$\Rightarrow\sqrt{{n}}=\sqrt{−{a}}={i}\sqrt{{a}}=\sqrt{{a}}\left({cos}\mathrm{0}.\mathrm{5}\pi+{isin}\mathrm{0}.\mathrm{5}\right)={e}^{\mathrm{0}.\mathrm{5}{i}\pi} \sqrt{{a}} \\ $$$$\Rightarrow\left(\sqrt{{n}}\right)^{{N}+\mathrm{1}} ={e}^{\mathrm{0}.\mathrm{5}{i}\pi\left({N}+\mathrm{1}\right)} \left(\sqrt{{a}}\right)^{{N}+\mathrm{1}} \\ $$$${Since}\:\mathrm{0}<{a}<\mathrm{1}\Rightarrow\left(\sqrt{{a}}\right)^{{N}+\mathrm{1}} \rightarrow\mathrm{0}\:{as}\:{N}\rightarrow\infty. \\ $$$$\therefore\underset{{N}\rightarrow\infty} {\mathrm{lim}}{S}\left({N}\right)=\frac{\mathrm{0}×{e}^{\infty{i}} −\sqrt{{n}}}{\sqrt{{n}}−\mathrm{1}}=\frac{\sqrt{{n}}}{\mathrm{1}−\sqrt{{n}}} \\ $$$${S}\left(\infty\right)=\frac{{i}\sqrt{{a}}}{\mathrm{1}−{i}\sqrt{{a}}}=\frac{{i}\sqrt{{a}}\left(\mathrm{1}+{i}\sqrt{{a}}\right)}{\mathrm{1}+{a}} \\ $$$${S}\left(\infty\right)=\frac{−{a}+{i}\sqrt{{a}}}{\mathrm{1}+{a}}=\frac{{n}+{i}\sqrt{−{n}}}{\mathrm{1}−{n}}.\Rightarrow{S}\left(\infty\right)\in\mathbb{C}. \\ $$$$ \\ $$$$\left(\mathrm{4}\right)\:{For}\:{n}\leqslant−\mathrm{1}\Rightarrow\left(\sqrt{{n}}\right)^{{N}+\mathrm{1}} \rightarrow{e}^{{i}\infty} \:{if}\:{n}=−\mathrm{1}. \\ $$$$\Rightarrow{a}=\mathrm{1}. \\ $$$${S}\left({N}\right)=\frac{\left(\sqrt{{n}}\right)^{{N}+\mathrm{1}} −\sqrt{{n}}}{\sqrt{{n}}−\mathrm{1}} \\ $$$$=\frac{\left({i}\sqrt{{a}}\right)^{{N}+\mathrm{1}} −{i}\sqrt{{a}}}{{i}\sqrt{{a}}−\mathrm{1}} \\ $$$$=\frac{{i}\sqrt{{a}}\left(\left({i}\sqrt{{a}}\right)^{{N}} −\mathrm{1}\right)}{{i}\sqrt{{a}}−\mathrm{1}} \\ $$$$=\frac{{i}\sqrt{{a}}\left(\mathrm{1}−{i}\sqrt{{a}}\right)\left(\mathrm{1}−\left({i}\sqrt{{a}}\right)^{{N}} \right)}{\mathrm{1}+{a}} \\ $$$$=\frac{\left({a}+{i}\sqrt{{a}}\right)\left(\mathrm{1}−\left({i}\sqrt{{a}}\right)^{{N}} \right)}{\mathrm{1}+{a}} \\ $$$$=\frac{{a}−{a}\left({i}\sqrt{{a}}\right)^{{N}} +{i}\sqrt{{a}}−\left({i}\sqrt{{a}}\right)^{{N}+\mathrm{1}} }{\mathrm{1}+{a}} \\ $$$$=\frac{{a}+{i}\sqrt{{a}}}{\mathrm{1}+{a}}−\frac{\left({i}\sqrt{{a}}\right)^{{N}} \left({a}+{i}\sqrt{{a}}\right)}{\mathrm{1}+{a}} \\ $$$${S}\left({N}\right)=\frac{{a}+{i}\sqrt{{a}}}{\mathrm{1}+{a}}\left(\mathrm{1}−{a}^{\mathrm{0}.\mathrm{5}{N}} {e}^{\mathrm{0}.\mathrm{5}\pi{iN}} \right) \\ $$$$\underset{{N}\rightarrow\infty} {\mathrm{lim}}{S}\left({N}\right)=\frac{\mathrm{1}+{i}}{\mathrm{2}}\left(\mathrm{1}−{e}^{{i}\infty} \right)\:{which}\:{is}\:{undefined} \\ $$$${since}\:{e}^{{i}\infty} \:{is}\:{indeterminate}. \\ $$$$ \\ $$$$\left(\mathrm{5}\right){If}\:{a}>\mathrm{1}\:{then}\:\underset{{N}\rightarrow\infty} {\mathrm{lim}}{S}\left({N}\right)=\frac{{a}+{i}\sqrt{{a}}}{\mathrm{1}+{a}}\left(\mathrm{1}−\infty{e}^{{i}\infty} \right) \\ $$$$\infty{e}^{{i}\infty} \:{is}\:{undefined}\Rightarrow{S}\left(\infty\right)\:{is}\:{undefined} \\ $$$${for}\:{n}\leqslant−\mathrm{1}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com