Question Number 47019 by ajfour last updated on 04/Nov/18
Commented by ajfour last updated on 04/Nov/18
$${If}\:{at}\:{its}\:{roots}\:\:{x}=−\mathrm{3}\:{and}\:{x}=\mathrm{2} \\ $$$${the}\:{biquadratic}\:{also}\:{has}\:{its} \\ $$$${points}\:{of}\:{inflexion},\:{find}\:{its} \\ $$$${other}\:{two}\:{roots}\:\alpha\:{and}\:\beta. \\ $$
Commented by ajfour last updated on 04/Nov/18
$${shown}\:{graph}\:{is}\:{just}\:{to}\:{help} \\ $$$${roughly}\:{depict}\:{the}\:{question}! \\ $$
Answered by MJS last updated on 04/Nov/18
$${y}={ax}^{\mathrm{4}} +{bx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+{e} \\ $$$${y}''=\mathrm{12}{ax}^{\mathrm{2}} +\mathrm{6}{bx}+\mathrm{2}{c} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{81}{a}−\mathrm{27}{b}+\mathrm{9}{c}−\mathrm{3}{d}+{e}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{16}{a}+\mathrm{8}{b}+\mathrm{4}{c}+\mathrm{2}{d}+{e}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{108}{a}−\mathrm{18}{b}+\mathrm{2}{c}=\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{48}{a}+\mathrm{12}{b}+\mathrm{2}{c}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$${y}={ax}^{\mathrm{4}} +\mathrm{2}{ax}^{\mathrm{3}} −\mathrm{36}{ax}^{\mathrm{2}} −\mathrm{37}{ax}+\mathrm{186}{a} \\ $$$${a}\left({x}+\mathrm{3}\right)\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{31}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\alpha=−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}};\:\beta=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
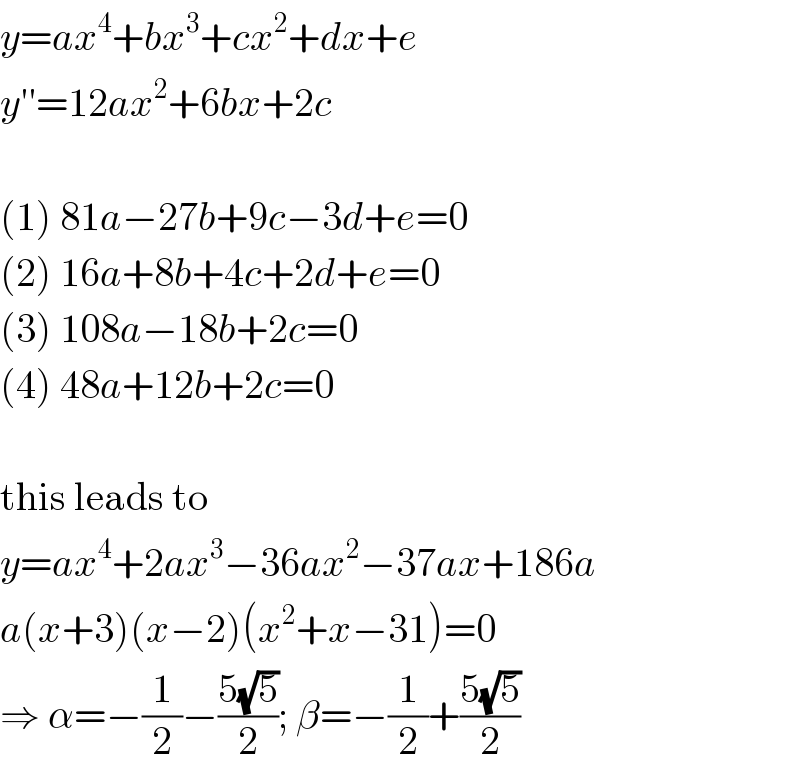
Commented by MJS last updated on 04/Nov/18
![(x+3)(x−2)(x+(1/2)+((5(√3))/2))(x+(1/2)−((5(√3))/2))= =x^4 +2x^3 −((47)/2)x^2 −((49)/2)x+111 (d^2 /dx^2 )[x^4 +2x^3 −((47)/2)x^2 −((49)/2)x+111]=12x^2 +12x−47 x=−3 ⇒ 12x^2 +12x−47=25 x=2 ⇒ 12x^2 +12x−47=25 so something went wrong](Q47051.png)
$$\left({x}+\mathrm{3}\right)\left({x}−\mathrm{2}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)= \\ $$$$={x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\frac{\mathrm{47}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{2}}{x}+\mathrm{111} \\ $$$$\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\frac{\mathrm{47}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{2}}{x}+\mathrm{111}\right]=\mathrm{12}{x}^{\mathrm{2}} +\mathrm{12}{x}−\mathrm{47} \\ $$$${x}=−\mathrm{3}\:\Rightarrow\:\mathrm{12}{x}^{\mathrm{2}} +\mathrm{12}{x}−\mathrm{47}=\mathrm{25} \\ $$$${x}=\mathrm{2}\:\Rightarrow\:\mathrm{12}{x}^{\mathrm{2}} +\mathrm{12}{x}−\mathrm{47}=\mathrm{25} \\ $$$$\mathrm{so}\:\mathrm{something}\:\mathrm{went}\:\mathrm{wrong} \\ $$
Commented by ajfour last updated on 04/Nov/18
$${yes}\:{Sir},\:{i}\:{got}\:{my}\:{error},\:{thanks}! \\ $$
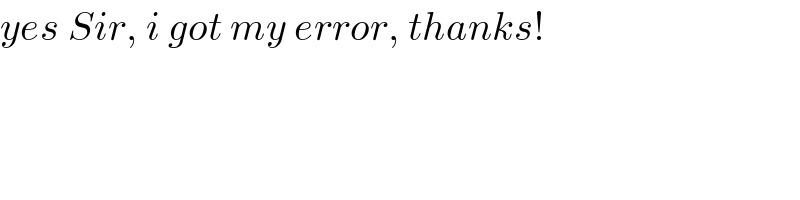
Commented by MJS last updated on 04/Nov/18
$$\mathrm{as}\:\mathrm{always},\:\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
Commented by peter frank last updated on 04/Nov/18
$$\mathrm{pls}\:\mathrm{help}\:\mathrm{QN}\:\mathrm{46813} \\ $$
Answered by ajfour last updated on 04/Nov/18
![y=a(x^2 +x−6)(x^2 +px+q) y ′=a(2x+1)(x^2 +px+q) +a(x^2 +x−6)(2x+p) y ′′=a[2(x^2 +px+q)+(2x+1)(2x+p) +(2x+1)(2x+p)+2(x^2 +x−6)] ⇒ y′′=2a[x^2 +px+q +(2x+1)(2x+p) +x^2 +x−6] ⇒ y′′=a[6x^2 +3(p+1)x+(q+p−6)] as its roots are x=−3, 2 ⇒ −(((p+1))/2) = −1 ⇒ p =1 and q+p−6 = −36 ⇒ q = −31 hence roots of x^2 +px+q =0 ⇒ x^2 +x−31=0 that is α, β are = ((−1±(√(1+124)))/2) = ((−1±5(√5))/2) .](Q47052.png)
$${y}={a}\left({x}^{\mathrm{2}} +{x}−\mathrm{6}\right)\left({x}^{\mathrm{2}} +{px}+{q}\right) \\ $$$${y}\:'={a}\left(\mathrm{2}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +{px}+{q}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:+{a}\left({x}^{\mathrm{2}} +{x}−\mathrm{6}\right)\left(\mathrm{2}{x}+{p}\right) \\ $$$${y}\:''={a}\left[\mathrm{2}\left({x}^{\mathrm{2}} +{px}+{q}\right)+\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}+{p}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:+\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}+{p}\right)+\mathrm{2}\left({x}^{\mathrm{2}} +{x}−\mathrm{6}\right)\right] \\ $$$$\Rightarrow\:{y}''=\mathrm{2}{a}\left[{x}^{\mathrm{2}} +{px}+{q}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}+{p}\right) \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{x}^{\mathrm{2}} +{x}−\mathrm{6}\right] \\ $$$$\Rightarrow\:{y}''={a}\left[\mathrm{6}{x}^{\mathrm{2}} +\mathrm{3}\left({p}+\mathrm{1}\right){x}+\left({q}+{p}−\mathrm{6}\right)\right] \\ $$$${as}\:{its}\:{roots}\:{are}\:{x}=−\mathrm{3},\:\mathrm{2} \\ $$$$\Rightarrow\:\:−\frac{\left({p}+\mathrm{1}\right)}{\mathrm{2}}\:=\:−\mathrm{1}\:\:\:\Rightarrow\:{p}\:=\mathrm{1} \\ $$$$\:\:{and}\:\:{q}+{p}−\mathrm{6}\:=\:−\mathrm{36} \\ $$$$\Rightarrow\:\:\:{q}\:=\:−\mathrm{31} \\ $$$$\:\:{hence}\:{roots}\:{of}\:{x}^{\mathrm{2}} +{px}+{q}\:=\mathrm{0} \\ $$$$\:\:\:\Rightarrow\:\:{x}^{\mathrm{2}} +{x}−\mathrm{31}=\mathrm{0} \\ $$$${that}\:{is}\:\alpha,\:\beta\:\:{are} \\ $$$$\:\:\:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{124}}}{\mathrm{2}}\:=\:\frac{−\mathrm{1}\pm\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\:. \\ $$