Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 4704 by lakshaysethi039 last updated on 25/Feb/16

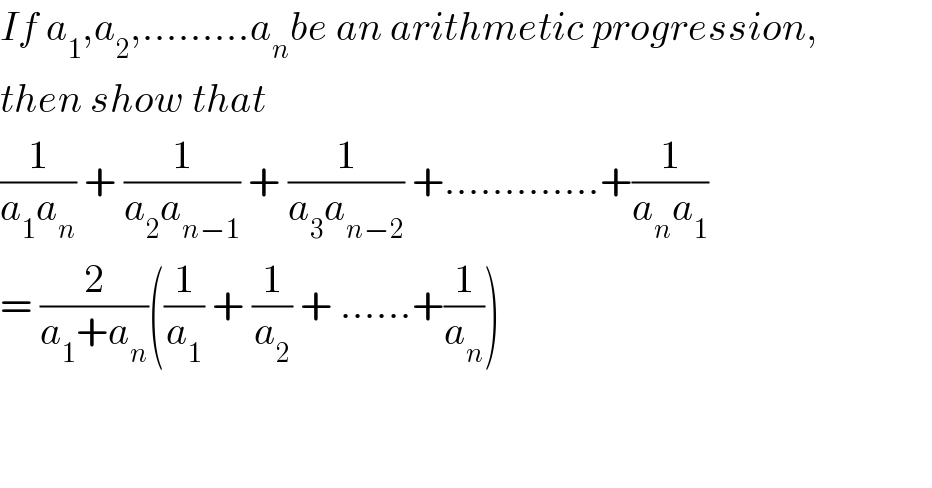
If a_1 ,a_2 ,.........a_n be an arithmetic progression, then show that (1/(a_1 a_n )) + (1/(a_2 a_(n−1) )) + (1/(a_3 a_(n−2) )) +.............+(1/(a_n a_1 )) = (2/(a_1 +a_n ))((1/a_1 ) + (1/a_2 ) + ......+(1/a_n ))

$${If}\:{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,.........{a}_{{n}} {be}\:{an}\:{arithmetic}\:{progression}, \\ $$$${then}\:{show}\:{that} \\ $$$$\frac{\mathrm{1}}{{a}_{\mathrm{1}} {a}_{{n}} }\:+\:\frac{\mathrm{1}}{{a}_{\mathrm{2}} {a}_{{n}−\mathrm{1}} }\:+\:\frac{\mathrm{1}}{{a}_{\mathrm{3}} {a}_{{n}−\mathrm{2}} }\:+.............+\frac{\mathrm{1}}{{a}_{{n}} {a}_{\mathrm{1}} }\: \\ $$$$=\:\frac{\mathrm{2}}{{a}_{\mathrm{1}} +{a}_{{n}} }\left(\frac{\mathrm{1}}{{a}_{\mathrm{1}} }\:+\:\frac{\mathrm{1}}{{a}_{\mathrm{2}} }\:+\:......+\frac{\mathrm{1}}{{a}_{{n}} }\right) \\ $$$$ \\ $$$$ \\ $$

Commented by Yozzii last updated on 25/Feb/16

Interesting property of A.Ps of non−zero terms. I′ve never seen this before.

$${Interesting}\:{property}\:{of}\:{A}.{Ps}\:{of}\: \\ $$$${non}−{zero}\:{terms}.\:{I}'{ve}\:{never}\:{seen}\:{this} \\ $$$${before}. \\ $$

Answered by Yozzii last updated on 25/Feb/16

Let S_n =Σ_(i=1) ^n a_i ^(−1) and J=(1/(a_1 a_n ))+(1/(a_2 a_(n−1) ))+(1/(a_3 a_(n−2) ))...+(1/(a_n a_1 )). First calculate sums that yield the denominators of terms of J in terms of a_i . (1) a_1 ^(−1) +a_n ^(−1) =((a_1 +a_n )/(a_1 a_n )) (2) a_2 ^(−1) +a_(n−1) ^(−1) =((a_2 +a_(n−1) )/(a_2 a_(n−1) )) (3) a_3 ^(−1) +a_(n−2) ^(−1) =((a_3 +a_(n−2) )/(a_3 a_(n−2) )) (4) a_4 ^(−1) +a_(n−3) ^(−1) =((a_4 +a_(n−3) )/(a_4 a_(n−3) )) ⋮ (n) a_n ^(−1) +a_1 ^(−1) =((a_n +a_1 )/(a_1 a_n )) Adding lines (1)→(n) we see that all a_i ^(−1) are added twice. Hence, we may write 2(Σ_(i=1) ^n a_i ^(−1) )=((a_1 +a_n )/(a_1 a_n ))+((a_2 +a_(n−1) )/(a_2 a_(n−1) ))+((a_3 +a_(n−2) )/(a_3 a_(n−2) ))+((a_4 +a_(n−3) )/(a_4 a_(n−3) ))+...+((a_n +a_1 )/(a_1 a_n )). (∗) We are given that {a_i }_(i=1) ^n is an arithmetic progression. Therefore, a_2 −a_1 =a_3 −a_2 =a_4 −a_3 =...=a_(n−2) −a_(n−3) =a_(n−1) −a_(n−2) =a_n −a_(n−1) . Using these equations we obtain a_2 −a_1 =a_n −a_(n−1 ) , or a_1 +a_n =a_2 +a_(n−1) . Similarly we have a_(n−1) −a_(n−2) =a_3 −a_2 so that a_(n−2) +a_3 =a_(n−1) +a_2 =a_1 +a_n . Also, a_(n−2) −a_(n−3) =a_4 −a_3 ⇒a_4 +a_(n−3) =a_3 +a_(n−2) =a_1 +a_n . Upon repeated use of this process we obtain the numerators of the terms on the r.h.s of (∗) all being equal to a_1 +a_n . ∴(a_1 +a_n ){(1/(a_1 a_n ))+(1/(a_2 a_(n−1) ))+(1/(a_3 a_(n−2) ))+(1/(a_4 a_(n−3) ))+...+(1/(a_1 a_n ))}=2S_n or (a_1 +a_n )J=2S_n ⇒J=(2/(a_1 +a_n ))S_n This is valid iff a_i ≠0 for 1≤i≤n. □

$${Let}\:{S}_{{n}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} ^{−\mathrm{1}} \:{and}\:{J}=\frac{\mathrm{1}}{{a}_{\mathrm{1}} {a}_{{n}} }+\frac{\mathrm{1}}{{a}_{\mathrm{2}} {a}_{{n}−\mathrm{1}} }+\frac{\mathrm{1}}{{a}_{\mathrm{3}} {a}_{{n}−\mathrm{2}} }...+\frac{\mathrm{1}}{{a}_{{n}} {a}_{\mathrm{1}} }. \\ $$$${First}\:{calculate}\:{sums}\:{that}\:{yield}\:{the}\: \\ $$$${denominators}\:{of}\:{terms}\:{of}\:{J}\:{in}\:{terms}\:{of}\:{a}_{{i}} . \\ $$$$\left(\mathrm{1}\right)\:{a}_{\mathrm{1}} ^{−\mathrm{1}} +{a}_{{n}} ^{−\mathrm{1}} =\frac{{a}_{\mathrm{1}} +{a}_{{n}} }{{a}_{\mathrm{1}} {a}_{{n}} } \\ $$$$\left(\mathrm{2}\right)\:{a}_{\mathrm{2}} ^{−\mathrm{1}} +{a}_{{n}−\mathrm{1}} ^{−\mathrm{1}} =\frac{{a}_{\mathrm{2}} +{a}_{{n}−\mathrm{1}} }{{a}_{\mathrm{2}} {a}_{{n}−\mathrm{1}} } \\ $$$$\left(\mathrm{3}\right)\:{a}_{\mathrm{3}} ^{−\mathrm{1}} +{a}_{{n}−\mathrm{2}} ^{−\mathrm{1}} =\frac{{a}_{\mathrm{3}} +{a}_{{n}−\mathrm{2}} }{{a}_{\mathrm{3}} {a}_{{n}−\mathrm{2}} } \\ $$$$\left(\mathrm{4}\right)\:{a}_{\mathrm{4}} ^{−\mathrm{1}} +{a}_{{n}−\mathrm{3}} ^{−\mathrm{1}} =\frac{{a}_{\mathrm{4}} +{a}_{{n}−\mathrm{3}} }{{a}_{\mathrm{4}} {a}_{{n}−\mathrm{3}} } \\ $$$$\vdots \\ $$$$\left({n}\right)\:{a}_{{n}} ^{−\mathrm{1}} +{a}_{\mathrm{1}} ^{−\mathrm{1}} =\frac{{a}_{{n}} +{a}_{\mathrm{1}} }{{a}_{\mathrm{1}} {a}_{{n}} } \\ $$$${Adding}\:{lines}\:\left(\mathrm{1}\right)\rightarrow\left({n}\right)\:{we}\:{see}\:{that}\: \\ $$$${all}\:{a}_{{i}} ^{−\mathrm{1}} \:{are}\:{added}\:{twice}.\:{Hence},\:{we}\:{may} \\ $$$${write}\: \\ $$$$\mathrm{2}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} ^{−\mathrm{1}} \right)=\frac{{a}_{\mathrm{1}} +{a}_{{n}} }{{a}_{\mathrm{1}} {a}_{{n}} }+\frac{{a}_{\mathrm{2}} +{a}_{{n}−\mathrm{1}} }{{a}_{\mathrm{2}} {a}_{{n}−\mathrm{1}} }+\frac{{a}_{\mathrm{3}} +{a}_{{n}−\mathrm{2}} }{{a}_{\mathrm{3}} {a}_{{n}−\mathrm{2}} }+\frac{{a}_{\mathrm{4}} +{a}_{{n}−\mathrm{3}} }{{a}_{\mathrm{4}} {a}_{{n}−\mathrm{3}} }+...+\frac{{a}_{{n}} +{a}_{\mathrm{1}} }{{a}_{\mathrm{1}} {a}_{{n}} }.\:\:\left(\ast\right) \\ $$$${We}\:{are}\:{given}\:{that}\:\left\{{a}_{{i}} \right\}_{{i}=\mathrm{1}} ^{{n}} \:{is}\:{an}\: \\ $$$${arithmetic}\:{progression}.\:{Therefore}, \\ $$$${a}_{\mathrm{2}} −{a}_{\mathrm{1}} ={a}_{\mathrm{3}} −{a}_{\mathrm{2}} ={a}_{\mathrm{4}} −{a}_{\mathrm{3}} =...={a}_{{n}−\mathrm{2}} −{a}_{{n}−\mathrm{3}} ={a}_{{n}−\mathrm{1}} −{a}_{{n}−\mathrm{2}} ={a}_{{n}} −{a}_{{n}−\mathrm{1}} . \\ $$$${Using}\:{these}\:{equations}\:{we}\:{obtain} \\ $$$${a}_{\mathrm{2}} −{a}_{\mathrm{1}} ={a}_{{n}} −{a}_{{n}−\mathrm{1}\:} ,\:{or}\:{a}_{\mathrm{1}} +{a}_{{n}} ={a}_{\mathrm{2}} +{a}_{{n}−\mathrm{1}} . \\ $$$${Similarly}\:{we}\:{have}\:{a}_{{n}−\mathrm{1}} −{a}_{{n}−\mathrm{2}} ={a}_{\mathrm{3}} −{a}_{\mathrm{2}} \\ $$$${so}\:{that}\:{a}_{{n}−\mathrm{2}} +{a}_{\mathrm{3}} ={a}_{{n}−\mathrm{1}} +{a}_{\mathrm{2}} ={a}_{\mathrm{1}} +{a}_{{n}} . \\ $$$${Also},\:{a}_{{n}−\mathrm{2}} −{a}_{{n}−\mathrm{3}} ={a}_{\mathrm{4}} −{a}_{\mathrm{3}} \\ $$$$\Rightarrow{a}_{\mathrm{4}} +{a}_{{n}−\mathrm{3}} ={a}_{\mathrm{3}} +{a}_{{n}−\mathrm{2}} ={a}_{\mathrm{1}} +{a}_{{n}} . \\ $$$${Upon}\:{repeated}\:{use}\:{of}\:{this}\:{process}\:{we} \\ $$$${obtain}\:{the}\:{numerators}\:{of}\:{the}\:{terms}\:{on} \\ $$$${the}\:{r}.{h}.{s}\:{of}\:\left(\ast\right)\:{all}\:{being}\:{equal}\:{to}\:{a}_{\mathrm{1}} +{a}_{{n}} . \\ $$$$\therefore\left({a}_{\mathrm{1}} +{a}_{{n}} \right)\left\{\frac{\mathrm{1}}{{a}_{\mathrm{1}} {a}_{{n}} }+\frac{\mathrm{1}}{{a}_{\mathrm{2}} {a}_{{n}−\mathrm{1}} }+\frac{\mathrm{1}}{{a}_{\mathrm{3}} {a}_{{n}−\mathrm{2}} }+\frac{\mathrm{1}}{{a}_{\mathrm{4}} {a}_{{n}−\mathrm{3}} }+...+\frac{\mathrm{1}}{{a}_{\mathrm{1}} {a}_{{n}} }\right\}=\mathrm{2}{S}_{{n}} \\ $$$${or}\:\left({a}_{\mathrm{1}} +{a}_{{n}} \right){J}=\mathrm{2}{S}_{{n}} \\ $$$$\Rightarrow{J}=\frac{\mathrm{2}}{{a}_{\mathrm{1}} +{a}_{{n}} }{S}_{{n}} \:\:\:\: \\ $$$${This}\:{is}\:{valid}\:{iff}\:{a}_{{i}} \neq\mathrm{0}\:{for}\:\mathrm{1}\leqslant{i}\leqslant{n}.\:\:\:\:\:\Box \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com