Question Number 47182 by maxmathsup by imad last updated on 05/Nov/18
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{x}} \sqrt{\mathrm{1}−\sqrt{{x}}}{dx}\: \\ $$
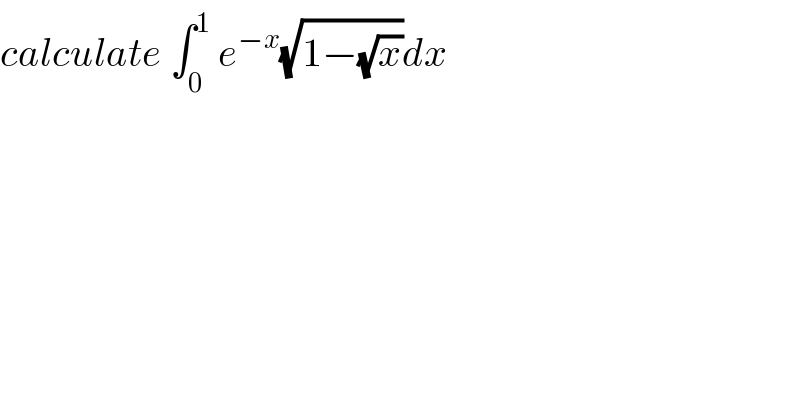
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Nov/18
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Nov/18
$${graph}\:{of}\:{e}^{−{x}} \sqrt{\mathrm{1}−\sqrt{{x}}\:} \\ $$$$\mathrm{0}.\mathrm{50}\:>\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}} \sqrt{\mathrm{1}−\sqrt{{x}}}\:\:{dx}>\mathrm{0} \\ $$
Commented by maxmathsup by imad last updated on 11/Nov/18
![let determine a approximat value of A =∫_0 ^1 e^(−x) (√(1−(√x)))dx we have e^u =1+(u/(1!)) +(u^2 /(2!)) +....⇒e^(−x) =1−x +(x^2 /2) −...⇒0≤ e^(−x) ≤1−x+(x^2 /2) ⇒ 0≤e^(−x) (√(1−(√x)))≤(1−x+(x^2 /2))(√(1−(√x))) ⇒0≤ ∫_0 ^1 e^(−x) (√(1−(√x)))dx≤∫_0 ^1 (1−x+(x^2 /2))(√(1−(√x)))dx changement (√(1−(√x)))=t give 1−(√x)=t^2 ⇒(√x)=1−t^2 ⇒x=(1−t^2 )^2 =t^4 −2t^2 +1 ⇒ ∫_0 ^1 (1−x+(x^2 /2))(√(1−(√x)))dx=−∫_0 ^1 (1−t^4 +2t^2 −1 +(((t^4 −2t^2 +1)^2 )/2))t(4t^3 −4t)dt =−2 ∫_0 ^1 (−2t^4 +4t^2 +( t^8 +4t^4 +1 +2(−2t^6 +t^4 −2t^2 )(t^4 −t^2 )dt =−2 ∫_0 ^1 (−2t^4 +4t^2 +t^8 +6t^4 −4t^6 −4t^2 +1)(t^4 −t^2 )dt =−2 ∫_0 ^1 (t^8 −4t^6 −2t^4 −4t^2 +1)(t^4 −t^2 )dt =−2 ∫_0 ^1 ( t^(12) −t^(10) −4t^(10) +4t^8 −2t^8 +2t^6 −4t^6 +4t^4 )dt =−2 ∫_0 ^1 (t^(12) −5t^(10) +2t^8 −2t^6 +4t^4 )dt =−2[(t^(13) /(13)) −((5t^(11) )/(11)) +((2t^9 )/9) −((2t^7 )/7) +((4t^5 )/5)]_0 ^1 =−2( (1/(13)) −(5/(11)) +(2/9) −(2/7) +(4/5))=−(2/(13)) +((10)/(11)) −(4/9) +(4/7) −(8/5) =α_0 ⇒0< A≤α_0](Q47545.png)
$${let}\:{determine}\:{a}\:{approximat}\:{value}\:{of}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{x}} \sqrt{\mathrm{1}−\sqrt{{x}}}{dx}\:{we}\:{have} \\ $$$${e}^{{u}} =\mathrm{1}+\frac{{u}}{\mathrm{1}!}\:+\frac{{u}^{\mathrm{2}} }{\mathrm{2}!}\:+....\Rightarrow{e}^{−{x}} =\mathrm{1}−{x}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:−...\Rightarrow\mathrm{0}\leqslant\:{e}^{−{x}} \leqslant\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{0}\leqslant{e}^{−{x}} \sqrt{\mathrm{1}−\sqrt{{x}}}\leqslant\left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sqrt{\mathrm{1}−\sqrt{{x}}}\:\Rightarrow\mathrm{0}\leqslant\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{x}} \sqrt{\mathrm{1}−\sqrt{{x}}}{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sqrt{\mathrm{1}−\sqrt{{x}}}{dx} \\ $$$${changement}\:\sqrt{\mathrm{1}−\sqrt{{x}}}={t}\:{give}\:\mathrm{1}−\sqrt{{x}}={t}^{\mathrm{2}} \:\Rightarrow\sqrt{{x}}=\mathrm{1}−{t}^{\mathrm{2}} \:\Rightarrow{x}=\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} ={t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sqrt{\mathrm{1}−\sqrt{{x}}}{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}\:+\frac{\left({t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\right){t}\left(\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}\right){dt} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{2}{t}^{\mathrm{4}} \:+\mathrm{4}{t}^{\mathrm{2}} \:+\left(\:{t}^{\mathrm{8}} +\mathrm{4}{t}^{\mathrm{4}} \:+\mathrm{1}\:+\mathrm{2}\left(−\mathrm{2}{t}^{\mathrm{6}} \:+{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \right)\left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} \right){dt}\right.\right. \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{2}{t}^{\mathrm{4}} \:+\mathrm{4}{t}^{\mathrm{2}} \:+{t}^{\mathrm{8}} \:+\mathrm{6}{t}^{\mathrm{4}} \:−\mathrm{4}{t}^{\mathrm{6}} −\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} \right){dt} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}^{\mathrm{8}} −\mathrm{4}{t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} \right){dt} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\:{t}^{\mathrm{12}} −{t}^{\mathrm{10}} −\mathrm{4}{t}^{\mathrm{10}} \:+\mathrm{4}{t}^{\mathrm{8}} \:−\mathrm{2}{t}^{\mathrm{8}} \:+\mathrm{2}{t}^{\mathrm{6}} −\mathrm{4}{t}^{\mathrm{6}} \:+\mathrm{4}{t}^{\mathrm{4}} \right){dt} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}^{\mathrm{12}} −\mathrm{5}{t}^{\mathrm{10}} \:+\mathrm{2}{t}^{\mathrm{8}} \:−\mathrm{2}{t}^{\mathrm{6}} \:+\mathrm{4}{t}^{\mathrm{4}} \right){dt} \\ $$$$=−\mathrm{2}\left[\frac{{t}^{\mathrm{13}} }{\mathrm{13}}\:−\frac{\mathrm{5}{t}^{\mathrm{11}} }{\mathrm{11}}\:+\frac{\mathrm{2}{t}^{\mathrm{9}} }{\mathrm{9}}\:−\frac{\mathrm{2}{t}^{\mathrm{7}} }{\mathrm{7}}\:+\frac{\mathrm{4}{t}^{\mathrm{5}} }{\mathrm{5}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\mathrm{2}\left(\:\frac{\mathrm{1}}{\mathrm{13}}\:−\frac{\mathrm{5}}{\mathrm{11}}\:+\frac{\mathrm{2}}{\mathrm{9}}\:−\frac{\mathrm{2}}{\mathrm{7}}\:+\frac{\mathrm{4}}{\mathrm{5}}\right)=−\frac{\mathrm{2}}{\mathrm{13}}\:+\frac{\mathrm{10}}{\mathrm{11}}\:−\frac{\mathrm{4}}{\mathrm{9}}\:+\frac{\mathrm{4}}{\mathrm{7}}\:−\frac{\mathrm{8}}{\mathrm{5}}\:=\alpha_{\mathrm{0}} \:\Rightarrow\mathrm{0}<\:{A}\leqslant\alpha_{\mathrm{0}} \\ $$