Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 4719 by prakash jain last updated on 29/Feb/16

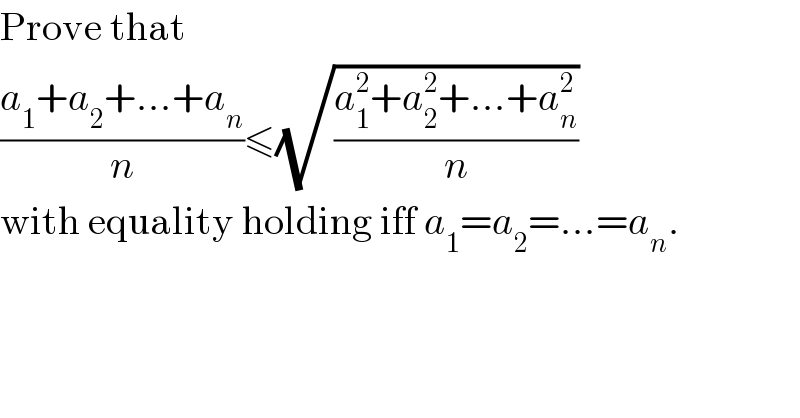
Prove that ((a_1 +a_2 +...+a_n )/n)≤(√((a_1 ^2 +a_2 ^2 +...+a_n ^2 )/n)) with equality holding iff a_1 =a_2 =...=a_n .

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\frac{{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...+{a}_{{n}} }{{n}}\leqslant\sqrt{\frac{{a}_{\mathrm{1}} ^{\mathrm{2}} +{a}_{\mathrm{2}} ^{\mathrm{2}} +...+{a}_{{n}} ^{\mathrm{2}} }{{n}}} \\ $$$$\mathrm{with}\:\mathrm{equality}\:\mathrm{holding}\:\mathrm{iff}\:{a}_{\mathrm{1}} ={a}_{\mathrm{2}} =...={a}_{{n}} . \\ $$

Commented by Yozzii last updated on 29/Feb/16

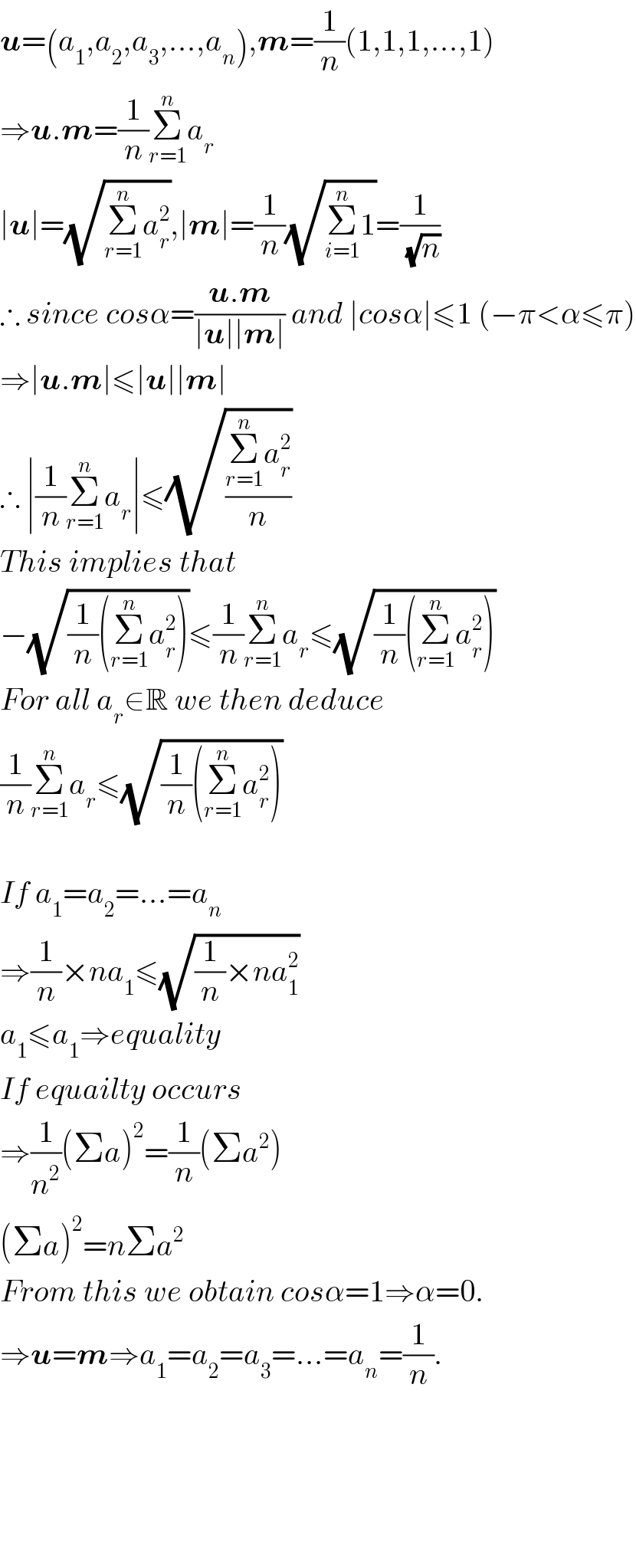
u=(a_1 ,a_2 ,a_3 ,...,a_n ),m=(1/n)(1,1,1,...,1) ⇒u.m=(1/n)Σ_(r=1) ^n a_r ∣u∣=(√(Σ_(r=1) ^n a_r ^2 )),∣m∣=(1/n)(√(Σ_(i=1) ^n 1))=(1/(√n)) ∴ since cosα=((u.m)/(∣u∣∣m∣)) and ∣cosα∣≤1 (−π<α≤π) ⇒∣u.m∣≤∣u∣∣m∣ ∴ ∣(1/n)Σ_(r=1) ^n a_r ∣≤(√((Σ_(r=1) ^n a_r ^2 )/n)) This implies that −(√((1/n)(Σ_(r=1) ^n a_r ^2 )))≤(1/n)Σ_(r=1) ^n a_r ≤(√((1/n)(Σ_(r=1) ^n a_r ^2 ))) For all a_r ∈R we then deduce (1/n)Σ_(r=1) ^n a_r ≤(√((1/n)(Σ_(r=1) ^n a_r ^2 ))) If a_1 =a_2 =...=a_n ⇒(1/n)×na_1 ≤(√((1/n)×na_1 ^2 )) a_1 ≤a_1 ⇒equality If equailty occurs ⇒(1/n^2 )(Σa)^2 =(1/n)(Σa^2 ) (Σa)^2 =nΣa^2 From this we obtain cosα=1⇒α=0. ⇒u=m⇒a_1 =a_2 =a_3 =...=a_n =(1/n).

$$\boldsymbol{{u}}=\left({a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,{a}_{\mathrm{3}} ,...,{a}_{{n}} \right),\boldsymbol{{m}}=\frac{\mathrm{1}}{{n}}\left(\mathrm{1},\mathrm{1},\mathrm{1},...,\mathrm{1}\right) \\ $$$$\Rightarrow\boldsymbol{{u}}.\boldsymbol{{m}}=\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} \\ $$$$\mid\boldsymbol{{u}}\mid=\sqrt{\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} ^{\mathrm{2}} },\mid\boldsymbol{{m}}\mid=\frac{\mathrm{1}}{{n}}\sqrt{\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1}}=\frac{\mathrm{1}}{\sqrt{{n}}} \\ $$$$\therefore\:{since}\:{cos}\alpha=\frac{\boldsymbol{{u}}.\boldsymbol{{m}}}{\mid\boldsymbol{{u}}\mid\mid\boldsymbol{{m}}\mid}\:{and}\:\mid{cos}\alpha\mid\leqslant\mathrm{1}\:\left(−\pi<\alpha\leqslant\pi\right) \\ $$$$\Rightarrow\mid\boldsymbol{{u}}.\boldsymbol{{m}}\mid\leqslant\mid\boldsymbol{{u}}\mid\mid\boldsymbol{{m}}\mid \\ $$$$\therefore\:\mid\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} \mid\leqslant\sqrt{\frac{\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} ^{\mathrm{2}} }{{n}}} \\ $$$${This}\:{implies}\:{that}\: \\ $$$$−\sqrt{\frac{\mathrm{1}}{{n}}\left(\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} ^{\mathrm{2}} \right)}\leqslant\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} \leqslant\sqrt{\frac{\mathrm{1}}{{n}}\left(\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} ^{\mathrm{2}} \right)} \\ $$$${For}\:{all}\:{a}_{{r}} \in\mathbb{R}\:{we}\:{then}\:{deduce}\: \\ $$$$\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} \leqslant\sqrt{\frac{\mathrm{1}}{{n}}\left(\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{r}} ^{\mathrm{2}} \right)} \\ $$$$ \\ $$$${If}\:{a}_{\mathrm{1}} ={a}_{\mathrm{2}} =...={a}_{{n}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{n}}×{na}_{\mathrm{1}} \leqslant\sqrt{\frac{\mathrm{1}}{{n}}×{na}_{\mathrm{1}} ^{\mathrm{2}} } \\ $$$${a}_{\mathrm{1}} \leqslant{a}_{\mathrm{1}} \Rightarrow{equality} \\ $$$${If}\:{equailty}\:{occurs} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\Sigma{a}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{{n}}\left(\Sigma{a}^{\mathrm{2}} \right) \\ $$$$\left(\Sigma{a}\right)^{\mathrm{2}} ={n}\Sigma{a}^{\mathrm{2}} \\ $$$${From}\:{this}\:{we}\:{obtain}\:{cos}\alpha=\mathrm{1}\Rightarrow\alpha=\mathrm{0}. \\ $$$$\Rightarrow\boldsymbol{{u}}=\boldsymbol{{m}}\Rightarrow{a}_{\mathrm{1}} ={a}_{\mathrm{2}} ={a}_{\mathrm{3}} =...={a}_{{n}} =\frac{\mathrm{1}}{{n}}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com