Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 4720 by prakash jain last updated on 29/Feb/16

Prove or counterexample that if a finite number of terms of a series are given then a infinite number of formulas for n^(th) term exists which satisfy the given finite number of terms. For example 33,9,33,44,? 4 terms are given if a_n =f(n) then there are infinite number of distinct f_k (n) such for all k. f_k (1)=a_1 ,f_k (2)=a_2 ,f_k (3)=a_3 ,f_k (4)=a_4 and there exists m∈N such thatf_k (m)≠f_j (m) if k≠j

$$\mathrm{Prove}\:\mathrm{or}\:\mathrm{counterexample}\:\mathrm{that}\:\mathrm{if}\:\mathrm{a}\:\mathrm{finite}\:\mathrm{number}\: \\ $$$$\mathrm{of}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{series}\:\mathrm{are}\:\mathrm{given}\:\mathrm{then}\:\mathrm{a}\:\mathrm{infinite}\:\mathrm{number} \\ $$$$\mathrm{of}\:\mathrm{formulas}\:\mathrm{for}\:{n}^{{th}} \:\mathrm{term}\:\mathrm{exists}\:\mathrm{which}\:\mathrm{satisfy} \\ $$$$\mathrm{the}\:\mathrm{given}\:\mathrm{finite}\:\mathrm{number}\:\mathrm{of}\:\mathrm{terms}. \\ $$$$\mathrm{For}\:\mathrm{example} \\ $$$$\mathrm{33},\mathrm{9},\mathrm{33},\mathrm{44},? \\ $$$$\mathrm{4}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{given}\:\mathrm{if}\:{a}_{{n}} ={f}\left({n}\right)\:\mathrm{then}\:\mathrm{there}\:\mathrm{are} \\ $$$$\mathrm{infinite}\:\mathrm{number}\:\mathrm{of}\:\mathrm{distinct}\:{f}_{{k}} \left({n}\right)\:\mathrm{such}\:\mathrm{for} \\ $$$$\mathrm{all}\:{k}. \\ $$$${f}_{{k}} \left(\mathrm{1}\right)={a}_{\mathrm{1}} ,{f}_{{k}} \left(\mathrm{2}\right)={a}_{\mathrm{2}} ,{f}_{{k}} \left(\mathrm{3}\right)={a}_{\mathrm{3}} ,{f}_{{k}} \left(\mathrm{4}\right)={a}_{\mathrm{4}} \\ $$$$\mathrm{and}\:\mathrm{there}\:\mathrm{exists}\:{m}\in\mathbb{N}\:\mathrm{such}\:\mathrm{that}{f}_{{k}} \left({m}\right)\neq{f}_{{j}} \left({m}\right)\: \\ $$$$\mathrm{if}\:{k}\neq{j} \\ $$

Answered by 123456 last updated on 29/Feb/16

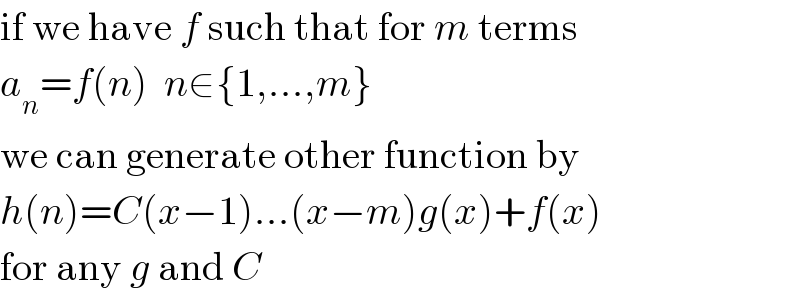
if we have f such that for m terms a_n =f(n) n∈{1,...,m} we can generate other function by h(n)=C(x−1)...(x−m)g(x)+f(x) for any g and C

$$\mathrm{if}\:\mathrm{we}\:\mathrm{have}\:{f}\:\mathrm{such}\:\mathrm{that}\:\mathrm{for}\:{m}\:\mathrm{terms} \\ $$$${a}_{{n}} ={f}\left({n}\right)\:\:{n}\in\left\{\mathrm{1},...,{m}\right\} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{generate}\:\mathrm{other}\:\mathrm{function}\:\mathrm{by} \\ $$$${h}\left({n}\right)={C}\left({x}−\mathrm{1}\right)...\left({x}−{m}\right){g}\left({x}\right)+{f}\left({x}\right) \\ $$$$\mathrm{for}\:\mathrm{any}\:{g}\:\mathrm{and}\:{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com