
Question and Answers Forum
Question Number 47266 by MrW3 last updated on 07/Nov/18

Commented by MrW3 last updated on 07/Nov/18

Answered by ajfour last updated on 08/Nov/18
![L_G ^� = ∫r^� ×(ω^� ×r^� )dm G being the centroid (mass center) and origin of x, y, z axes is G. L_G = ∫[(r^� .r^� )ω^� −(ω^� .r^� )r^� ]dm l^� = ai^� +bj^� +ck^� ; r^� =xi^� +yj^� +zk^� ω^� = ω((l^� /l)) L^� =(ω/l)∫[(ai^� +bj^� +ck^� )(x^2 +y^2 +z^2 ) −(xi^� +yj^� +zk^� )(ax+by+cz)]dm =(ω/l)∫ Σ{[a(y^2 +z^2 )−x(by+cz)]i^� }dm = ((𝛒 ω)/l)∫_(−c/2) ^( c/2) ∫_(−b/2) ^( b/2) ∫_(−a/2) ^( a/2) ( Σ{[a(y^2 +z^2 )−x(by+cz)]i^� )dxdydz =((ρ ω)/l)∫∫_(−b/2) ^( b/2) (Σ{a^2 (y^2 +z^2 )}i^� )dydz =((ρω)/l)∫_(−c/2) ^( c/2) (Σ{a^2 ((b^3 /(12))+bz^2 )}i^� )dz =((ρω)/l)Σ{a^2 (((b^3 c)/(12))+((bc^3 )/(12)))}i^� = ((ρ ω)/l)Σ{a[((abc)/(12))(b^2 +c^2 )]}i^� =((ρω)/l)×((abc)/(12)){a(b^2 +c^2 )i^� +b(c^2 +a^2 )j^� +c(a^2 +b^2 )k^� } L_G ^� = ((ρabcω)/(12(√(a^2 +b^2 +c^2 ))))Σ{a(b^2 +c^2 )i^� } and since ρabc = M L_G ^� = ((Mω)/(12(√(a^2 +b^2 +c^2 ))))Σ{a(b^2 +c^2 )i^� } Generally L_G ^� = ∫r^� ×(ω^� ×r^� )dm = ∫(xi^� +yj^� +zk^� )× determinant ((i^� ,j^� ,k^� ),(ω_x ,ω_y ,ω_z ),(x,y,z))dm =∫ determinant ((i^� ,j^� ,k^� ),(x,y,z),((ω_y z−ω_z y),(ω_z x−ω_x z),(ω_x y−ω_y x)))dm =Σ[∫{y(ω_x y−ω_y x)−z(ω_z x−ω_x z)}dm]i^� =Σ[∫{ω_x (y^2 +z^2 )−ω_y (xy)−ω_z (zx)}dm]i^� and since I_x =∫(y^2 +z^2 )dm I_(xy) = ∫xydm L_x = I_x ω_x −I_(xy) ω_y −I_(zx) ω_z L_y = −I_(xy) ω_x +I_y ω_y −I_(yz) ω_z L_z = −I_(zx) ω_x −I_(yz) ω_y +I_z ω_z Inertia tensor is ((I_x ,(−I_(xy) ),(−I_(zx) )),((−I_(xy) ),I_y ,(−I_(yz) )),((−I_(zx) ),(−I_(yz) ),I_z ) ) For this very question Inertia tensor is ((((M/(12))(b^2 +c^2 )),0,0),(0,((M/(12))(c^2 +a^2 )),0),(0,0,((M/(12))(a^2 +b^2 ))) ) If chosen coordinate system is Gxyz , the pricipal axes of inertia_(−−−−−−−−−−−−−−−−) , then the centroidal mass products of inertia of a body with respect to these prinxipal axes of inertia, are zero. I_(xy) = I_(yz) = I_(zx) = 0 . And I_x , I_y , I_z are called the principal centroidal moments of ineetia of the body. About any other point fixed point O L_O ^� = r^� ×mv_(cm) ^� +L_G ^� r^� being the position vector of G relative to O. _________________________.](Q47271.png)
Commented by MrW3 last updated on 07/Nov/18
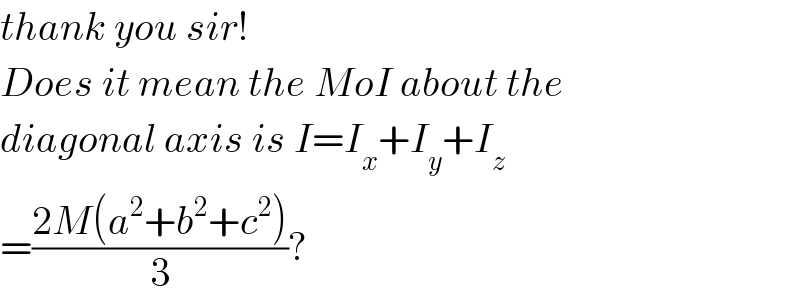
Commented by ajfour last updated on 08/Nov/18
![No, MoI will be a tensor for asymmetric orientations (9 components) We need MoI to know angular momentum: For x- component L_x , we just need to attach ω_x , ω_y , and ω_z respectively to each element in first row of the inertia tensor found. similarly for L_y and L_z we shall rather use respectively the 2^(nd) and 3^(rd) row. L_x =Mω_x ( ((b^2 +c^2 )/(12))) L_x = ((Mω)/(√(a^2 +b^2 +c^2 ))){a(((b^2 +c^2 )/(12)))} L_x =((Mωa(b^2 +c^2 ))/(12(√(a^2 +b^2 +c^2 )))) = ((Mω)/(12))(b^2 +c^2 )cos α α being angle of diagonal with x- axes. So L_(diagonal) =ΣL_x cos α = ((Mω)/(12))[((a^2 (b^2 +c^2 )+b^2 (c^2 +a^2 )+c^2 (a^2 +b^2 ))/(a^2 +b^2 +c^2 ))] If b=c=a we get I_(diagonal) = ((Ma^2 )/6) .](Q47281.png)
Commented by mr W last updated on 07/Nov/18

Commented by mr W last updated on 07/Nov/18

Commented by ajfour last updated on 08/Nov/18

