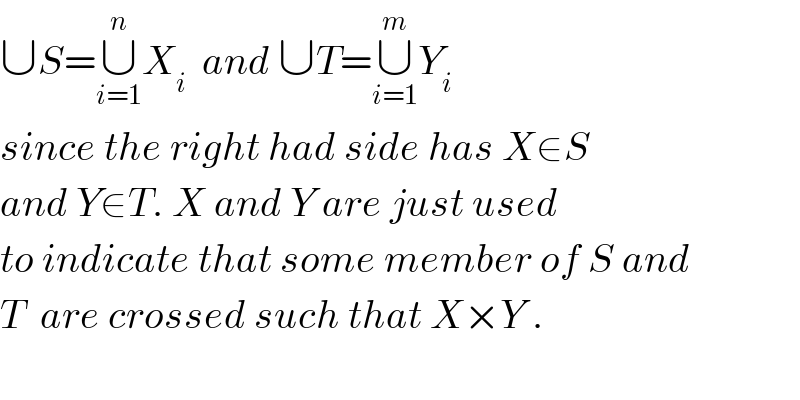Question and Answers Forum
Question Number 4733 by Yozzii last updated on 02/Mar/16

Commented by Yozzii last updated on 02/Mar/16
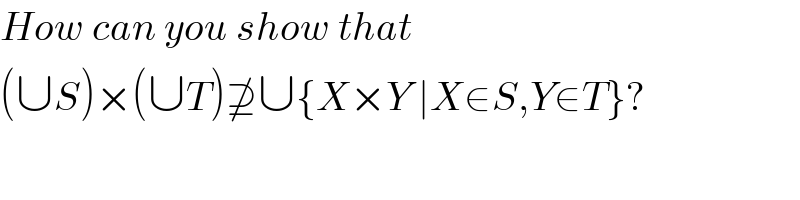
Commented by prakash jain last updated on 02/Mar/16

Commented by Yozzii last updated on 02/Mar/16

Commented by prakash jain last updated on 02/Mar/16
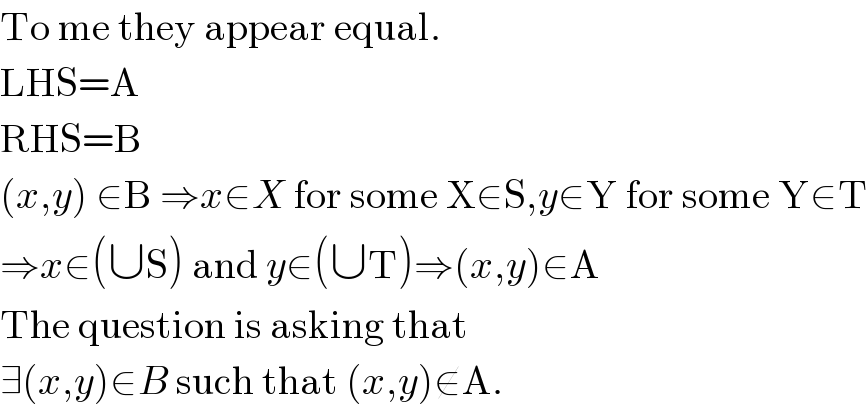
Commented by Yozzii last updated on 02/Mar/16
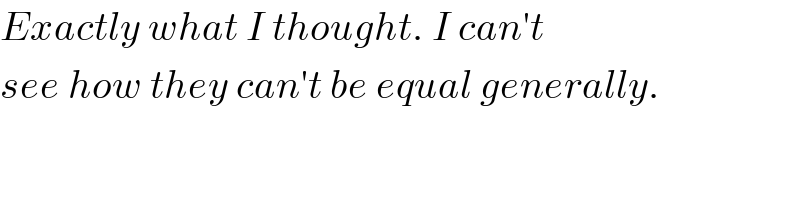
Commented by prakash jain last updated on 04/Mar/16

Commented by 123456 last updated on 04/Mar/16
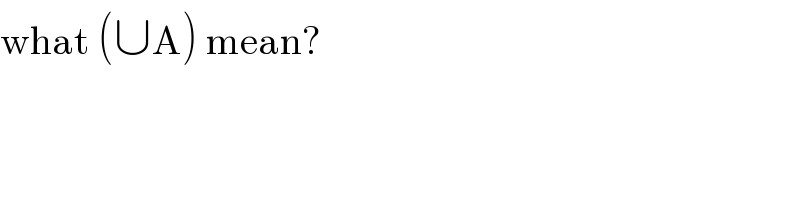
Commented by Yozzii last updated on 04/Mar/16
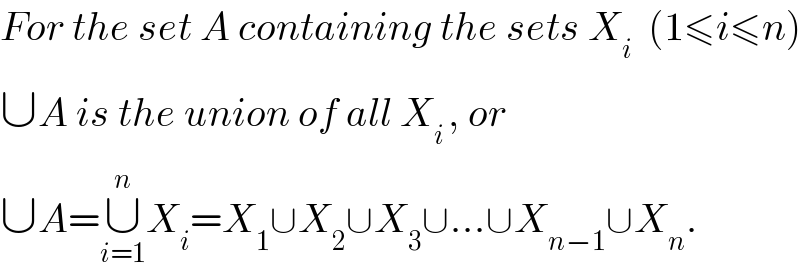
Commented by 123456 last updated on 04/Mar/16
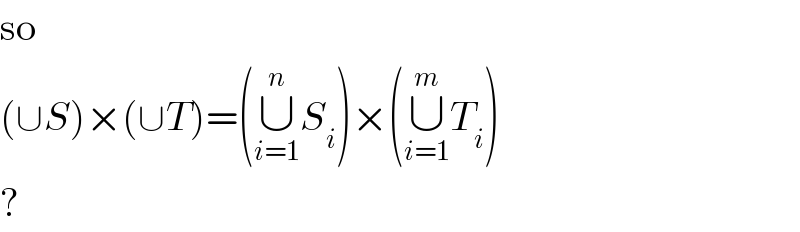
Commented by Yozzii last updated on 04/Mar/16