Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 47433 by Tawa1 last updated on 09/Nov/18

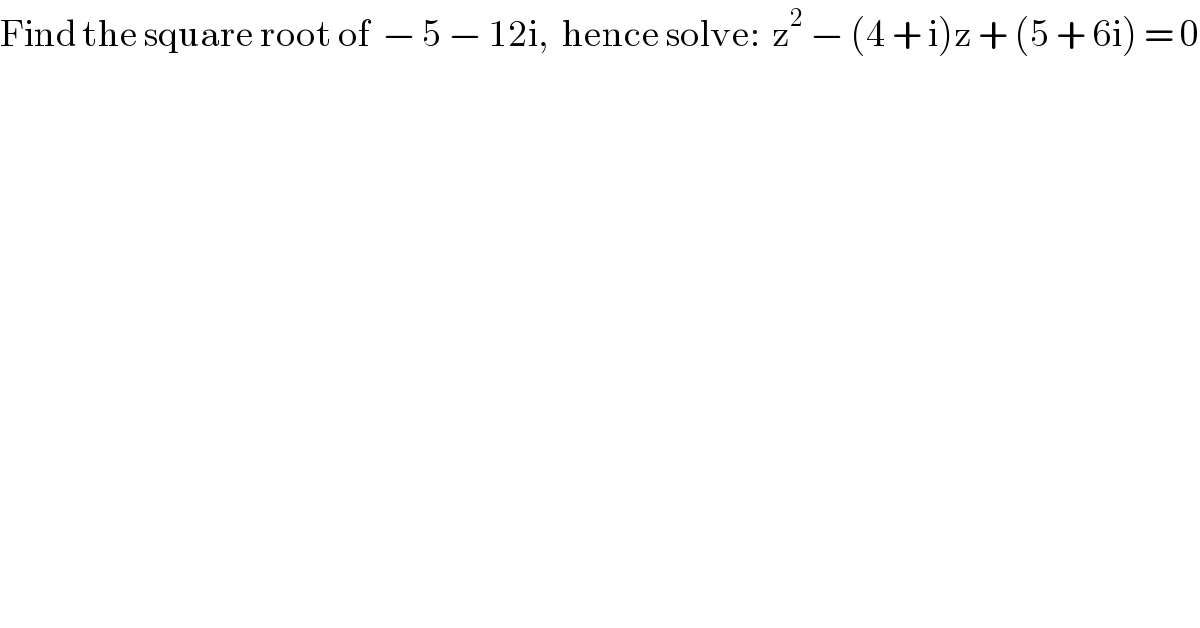
Find the square root of − 5 − 12i, hence solve: z^2 − (4 + i)z + (5 + 6i) = 0

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{square}\:\mathrm{root}\:\mathrm{of}\:\:−\:\mathrm{5}\:−\:\mathrm{12i},\:\:\mathrm{hence}\:\mathrm{solve}:\:\:\mathrm{z}^{\mathrm{2}} \:−\:\left(\mathrm{4}\:+\:\mathrm{i}\right)\mathrm{z}\:+\:\left(\mathrm{5}\:+\:\mathrm{6i}\right)\:=\:\mathrm{0} \\ $$

Commented by peter frank last updated on 10/Nov/18

let a+ib=(√(-5−12i)) a^2 −b^2 +2abi=-5−12i by comparison a^2 −b^2 =-5......(1) 2abi=-12i⇒2ab=-12....(2) a=(±2 or±3) b=(±3 or±2) a+ib=±(2+3i) or±(3+2i)

$$\mathrm{let}\:\mathrm{a}+\mathrm{ib}=\sqrt{-\mathrm{5}−\mathrm{12i}} \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} +\mathrm{2abi}=-\mathrm{5}−\mathrm{12i} \\ $$$$\mathrm{by}\:\mathrm{comparison} \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} =-\mathrm{5}......\left(\mathrm{1}\right) \\ $$$$\mathrm{2abi}=-\mathrm{12i}\Rightarrow\mathrm{2ab}=-\mathrm{12}....\left(\mathrm{2}\right) \\ $$$$\mathrm{a}=\left(\pm\mathrm{2}\:\mathrm{or}\pm\mathrm{3}\right) \\ $$$$\mathrm{b}=\left(\pm\mathrm{3}\:\mathrm{or}\pm\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\mathrm{a}+\mathrm{ib}=\pm\left(\mathrm{2}+\mathrm{3i}\right)\:\mathrm{or}\pm\left(\mathrm{3}+\mathrm{2i}\right) \\ $$$$ \\ $$$$ \\ $$

Commented by Tawa1 last updated on 10/Nov/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by maxmathsup by imad last updated on 10/Nov/18

∣−5−12i∣=(√(25+144))=(√(169))=13 ⇒−5−12i =13(−(5/(13)) −((12)/(13))i)=r e^(iπ) ((5/(13))+((12)/(13))i)and (5/(13))+((12)/(13))i=e^(iθ) wih r=13 and cosθ =−(5/(13)) and sinθ =−((12)/(13)) ⇒tanθ=((12)/5) and r=13 and θ=arctan(((12)/(5 ))) ⇒−5−12i =13e^(i(π +arctan(((12)/5))) ⇒ (√(−5−12i))=+^− (√(13))e^(i((π/2)+(1/2)arctan(((12)/5)))) for the equation z^2 −(4+i)z+5+6i =0 Δ =(4+i)^2 −4(5+6i) =16+8i−1−20−24i =−5+16i ⇒ z_1 =((4+i+(√(−5+16i)))/2) and z_2 =((4+i−(√(−5+16i)))/2) we see there no relation between the 2 Questions..

$$\mid−\mathrm{5}−\mathrm{12}{i}\mid=\sqrt{\mathrm{25}+\mathrm{144}}=\sqrt{\mathrm{169}}=\mathrm{13}\:\Rightarrow−\mathrm{5}−\mathrm{12}{i}\:=\mathrm{13}\left(−\frac{\mathrm{5}}{\mathrm{13}}\:−\frac{\mathrm{12}}{\mathrm{13}}{i}\right)={r}\:{e}^{{i}\pi} \left(\frac{\mathrm{5}}{\mathrm{13}}+\frac{\mathrm{12}}{\mathrm{13}}{i}\right){and} \\ $$$$\frac{\mathrm{5}}{\mathrm{13}}+\frac{\mathrm{12}}{\mathrm{13}}{i}={e}^{{i}\theta} \:\:\:{wih}\:{r}=\mathrm{13}\:{and}\:{cos}\theta\:=−\frac{\mathrm{5}}{\mathrm{13}}\:\:{and}\:{sin}\theta\:=−\frac{\mathrm{12}}{\mathrm{13}}\:\Rightarrow{tan}\theta=\frac{\mathrm{12}}{\mathrm{5}} \\ $$$${and}\:{r}=\mathrm{13}\:{and}\:\theta={arctan}\left(\frac{\mathrm{12}}{\mathrm{5}\:}\right)\:\Rightarrow−\mathrm{5}−\mathrm{12}{i}\:=\mathrm{13}{e}^{{i}\left(\pi\:+{arctan}\left(\frac{\mathrm{12}}{\mathrm{5}}\right)\right.} \:\Rightarrow \\ $$$$\sqrt{−\mathrm{5}−\mathrm{12}{i}}=\overset{−} {+}\sqrt{\mathrm{13}}{e}^{{i}\left(\frac{\pi}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{12}}{\mathrm{5}}\right)\right)} \\ $$$${for}\:{the}\:{equation}\:{z}^{\mathrm{2}} −\left(\mathrm{4}+{i}\right){z}+\mathrm{5}+\mathrm{6}{i}\:=\mathrm{0} \\ $$$$\Delta\:=\left(\mathrm{4}+{i}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{5}+\mathrm{6}{i}\right)\:=\mathrm{16}+\mathrm{8}{i}−\mathrm{1}−\mathrm{20}−\mathrm{24}{i}\:=−\mathrm{5}+\mathrm{16}{i}\:\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =\frac{\mathrm{4}+{i}+\sqrt{−\mathrm{5}+\mathrm{16}{i}}}{\mathrm{2}}\:{and}\:{z}_{\mathrm{2}} =\frac{\mathrm{4}+{i}−\sqrt{−\mathrm{5}+\mathrm{16}{i}}}{\mathrm{2}} \\ $$$${we}\:{see}\:{there}\:{no}\:{relation}\:{between}\:{the}\:\mathrm{2}\:{Questions}.. \\ $$

Commented by Tawa1 last updated on 10/Nov/18

God bless you sir. The correct question should be. z^2 − (4 + i)z + (5 + 5i) = 0. Please check sir. God bless you

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\:\mathrm{The}\:\mathrm{correct}\:\mathrm{question}\:\mathrm{should}\:\mathrm{be}. \\ $$$$\mathrm{z}^{\mathrm{2}} \:−\:\left(\mathrm{4}\:+\:\mathrm{i}\right)\mathrm{z}\:+\:\left(\mathrm{5}\:+\:\mathrm{5i}\right)\:=\:\mathrm{0}.\:\:\:\:\:\mathrm{Please}\:\mathrm{check}\:\mathrm{sir}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$

Commented by maxmathsup by imad last updated on 10/Nov/18

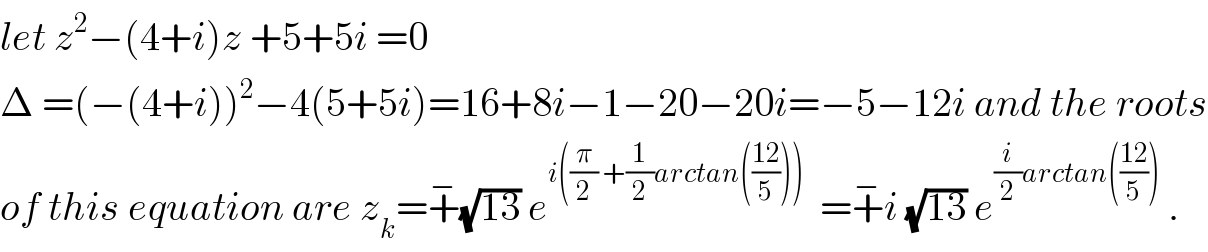
let z^2 −(4+i)z +5+5i =0 Δ =(−(4+i))^2 −4(5+5i)=16+8i−1−20−20i=−5−12i and the roots of this equation are z_k =+^− (√(13)) e^(i((π/2) +(1/2)arctan(((12)/5)))) =+^− i (√(13)) e^((i/2)arctan(((12)/5))) .

$${let}\:{z}^{\mathrm{2}} −\left(\mathrm{4}+{i}\right){z}\:+\mathrm{5}+\mathrm{5}{i}\:=\mathrm{0} \\ $$$$\Delta\:=\left(−\left(\mathrm{4}+{i}\right)\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{5}+\mathrm{5}{i}\right)=\mathrm{16}+\mathrm{8}{i}−\mathrm{1}−\mathrm{20}−\mathrm{20}{i}=−\mathrm{5}−\mathrm{12}{i}\:{and}\:{the}\:{roots} \\ $$$${of}\:{this}\:{equation}\:{are}\:{z}_{{k}} =\overset{−} {+}\sqrt{\mathrm{13}}\:{e}^{{i}\left(\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{12}}{\mathrm{5}}\right)\right)} \:\:=\overset{−} {+}{i}\:\sqrt{\mathrm{13}}\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{12}}{\mathrm{5}}\right)} \:. \\ $$

Commented by Tawa1 last updated on 10/Nov/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by Smail last updated on 10/Nov/18

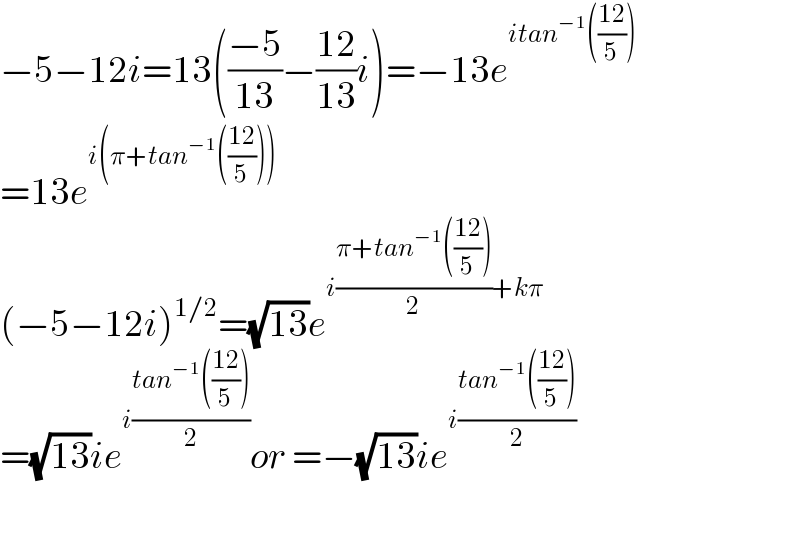
−5−12i=13(((−5)/(13))−((12)/(13))i)=−13e^(itan^(−1) (((12)/5))) =13e^(i(π+tan^(−1) (((12)/5)))) (−5−12i)^(1/2) =(√(13))e^(i((π+tan^(−1) (((12)/5)))/2)+kπ) =(√(13))ie^(i((tan^(−1) (((12)/5)))/2)) or =−(√(13))ie^(i((tan^(−1) (((12)/5)))/2))

$$−\mathrm{5}−\mathrm{12}{i}=\mathrm{13}\left(\frac{−\mathrm{5}}{\mathrm{13}}−\frac{\mathrm{12}}{\mathrm{13}}{i}\right)=−\mathrm{13}{e}^{{itan}^{−\mathrm{1}} \left(\frac{\mathrm{12}}{\mathrm{5}}\right)} \\ $$$$=\mathrm{13}{e}^{{i}\left(\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{12}}{\mathrm{5}}\right)\right)} \\ $$$$\left(−\mathrm{5}−\mathrm{12}{i}\right)^{\mathrm{1}/\mathrm{2}} =\sqrt{\mathrm{13}}{e}^{{i}\frac{\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{12}}{\mathrm{5}}\right)}{\mathrm{2}}+{k}\pi} \\ $$$$=\sqrt{\mathrm{13}}{ie}^{{i}\frac{{tan}^{−\mathrm{1}} \left(\frac{\mathrm{12}}{\mathrm{5}}\right)}{\mathrm{2}}} {or}\:=−\sqrt{\mathrm{13}}{ie}^{{i}\frac{{tan}^{−\mathrm{1}} \left(\frac{\mathrm{12}}{\mathrm{5}}\right)}{\mathrm{2}}} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 10/Nov/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com