Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 4751 by Yozzii last updated on 04/Mar/16

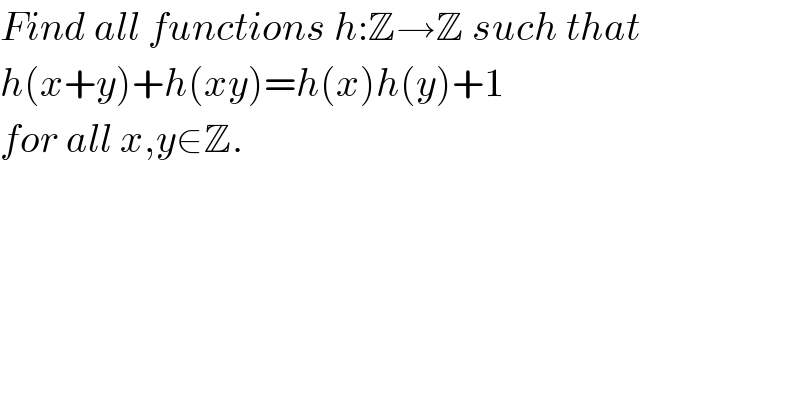
Find all functions h:Z→Z such that h(x+y)+h(xy)=h(x)h(y)+1 for all x,y∈Z.

$${Find}\:{all}\:{functions}\:{h}:\mathbb{Z}\rightarrow\mathbb{Z}\:{such}\:{that} \\ $$$${h}\left({x}+{y}\right)+{h}\left({xy}\right)={h}\left({x}\right){h}\left({y}\right)+\mathrm{1} \\ $$$${for}\:{all}\:{x},{y}\in\mathbb{Z}. \\ $$

Commented by prakash jain last updated on 06/Mar/16

y=0 h(x)+h(0)=h(x)h(0)+1 h(x)(1−h(0))=1−h(0) ⇒h(x)=1 or h(0)=1 One solution h(x)=1 case 2: h(0)=1 y=−x h(0)+h(−x^2 )=[h(x)][h(−x)]+1 h(x)h(−x)=h(−x^2 )

$${y}=\mathrm{0} \\ $$$${h}\left({x}\right)+{h}\left(\mathrm{0}\right)={h}\left({x}\right){h}\left(\mathrm{0}\right)+\mathrm{1} \\ $$$${h}\left({x}\right)\left(\mathrm{1}−{h}\left(\mathrm{0}\right)\right)=\mathrm{1}−{h}\left(\mathrm{0}\right) \\ $$$$\Rightarrow{h}\left({x}\right)=\mathrm{1}\:{or}\:{h}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{One}\:\mathrm{solution}\:{h}\left({x}\right)=\mathrm{1} \\ $$$${case}\:\mathrm{2}:\:{h}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${y}=−{x} \\ $$$${h}\left(\mathrm{0}\right)+{h}\left(−{x}^{\mathrm{2}} \right)=\left[{h}\left({x}\right)\right]\left[{h}\left(−{x}\right)\right]+\mathrm{1} \\ $$$${h}\left({x}\right){h}\left(−{x}\right)={h}\left(−{x}^{\mathrm{2}} \right) \\ $$

Commented by prakash jain last updated on 07/Mar/16

Since only integers are required h(0)=1 x=1,y=−1 h(0)+h(−1)=h(1)h(−1)+1⇒h(1)=1 or h(−1)=0 case h(1)=1 h(n+1)+h(n)=h(n)h(1)+1 h(n+1)=1 ⇒h(x)=1 for x≥0 ...(A) Let h(−1)=k x=−2,y=1 h(−1)+h(−2)=h(−1)h(1)+1 h(−2)=1 x=−1,y=−1 h(−2)+h(1)=h(−1)h(1)+1 h(−2)=k x=1,y=−3 h(−2)+h(−3)=h(−3)h(1)+1 h(−2)=1⇒k=1 x=−2,y=−1 h(−3)+h(2)=h(−2)h(1)+1⇒h(−3)=1 if h(1)=1⇒h(x)=1 ∀x∈Z case h(−1)=0 Corrections in blue. x=2,y=−1 h(1)+h(−2)=h(2)h(−1)+1 x=−n,y=−1 h(−n−1)+h(−n)=h(−n)h(−1)+1 h(−n−1)=−h(−n) The above line also wrong h(−1)=0 h(−n−1)=1−h(−n) ⇒h(1)=1 (wrong) ⇒h(x)=1 contradicts h(−1)=0 too many mistakes in handling h(−1)=0 will redo. So it looks like h(x)=1 is the only solution. Are there any other solutions in answer?

$$\mathrm{Since}\:\mathrm{only}\:\mathrm{integers}\:\mathrm{are}\:\mathrm{required}\: \\ $$$${h}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${x}=\mathrm{1},{y}=−\mathrm{1} \\ $$$${h}\left(\mathrm{0}\right)+{h}\left(−\mathrm{1}\right)={h}\left(\mathrm{1}\right){h}\left(−\mathrm{1}\right)+\mathrm{1}\Rightarrow{h}\left(\mathrm{1}\right)=\mathrm{1}\:{or}\:{h}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$${case}\:{h}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:{h}\left({n}+\mathrm{1}\right)+{h}\left({n}\right)={h}\left({n}\right){h}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$$\:\:\:\:\:\:{h}\left({n}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\Rightarrow{h}\left({x}\right)=\mathrm{1}\:{for}\:{x}\geqslant\mathrm{0}\:\:\:...\left({A}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{Let}\:{h}\left(−\mathrm{1}\right)={k} \\ $$$$\:\:\:\:\:\:\:{x}=−\mathrm{2},{y}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{h}\left(−\mathrm{1}\right)+{h}\left(−\mathrm{2}\right)={h}\left(−\mathrm{1}\right){h}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{h}\left(−\mathrm{2}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{x}=−\mathrm{1},{y}=−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{h}\left(−\mathrm{2}\right)+{h}\left(\mathrm{1}\right)={h}\left(−\mathrm{1}\right){h}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{h}\left(−\mathrm{2}\right)={k} \\ $$$$\:\:\:\:\:\:{x}=\mathrm{1},{y}=−\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{h}\left(−\mathrm{2}\right)+{h}\left(−\mathrm{3}\right)={h}\left(−\mathrm{3}\right){h}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{h}\left(−\mathrm{2}\right)=\mathrm{1}\Rightarrow{k}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{x}=−\mathrm{2},{y}=−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{h}\left(−\mathrm{3}\right)+{h}\left(\mathrm{2}\right)={h}\left(−\mathrm{2}\right){h}\left(\mathrm{1}\right)+\mathrm{1}\Rightarrow{h}\left(−\mathrm{3}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{if}\:{h}\left(\mathrm{1}\right)=\mathrm{1}\Rightarrow{h}\left({x}\right)=\mathrm{1}\:\forall{x}\in\mathbb{Z} \\ $$$${case}\:{h}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{Corrections}\:\mathrm{in}\:\mathrm{blue}. \\ $$$$\:\:\:\:\:{x}=\mathrm{2},{y}=−\mathrm{1} \\ $$$$\:\:\:\:\:{h}\left(\mathrm{1}\right)+{h}\left(−\mathrm{2}\right)={h}\left(\mathrm{2}\right){h}\left(−\mathrm{1}\right)+\mathrm{1} \\ $$$$\:\:\:\:\:{x}=−{n},{y}=−\mathrm{1} \\ $$$$\:\:\:\:\:{h}\left(−{n}−\mathrm{1}\right)+{h}\left(−{n}\right)={h}\left(−{n}\right){h}\left(−\mathrm{1}\right)+\mathrm{1} \\ $$$$\:\:\:\:\:{h}\left(−{n}−\mathrm{1}\right)=−{h}\left(−{n}\right) \\ $$$$\:\:\:\:\:\mathrm{The}\:\mathrm{above}\:\mathrm{line}\:\mathrm{also}\:\mathrm{wrong}\:{h}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:{h}\left(−{n}−\mathrm{1}\right)=\mathrm{1}−{h}\left(−{n}\right) \\ $$$$\:\:\:\:\:\Rightarrow{h}\left(\mathrm{1}\right)=\mathrm{1}\:\left({wrong}\right) \\ $$$$\:\:\:\:\:\Rightarrow{h}\left({x}\right)=\mathrm{1}\:{contradicts}\:{h}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:{too}\:{many}\:{mistakes}\:{in}\:{handling}\:{h}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:{will}\:{redo}. \\ $$$$\mathrm{So}\:\mathrm{it}\:\mathrm{looks}\:\mathrm{like}\:{h}\left({x}\right)=\mathrm{1}\:\mathrm{is}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}. \\ $$$$\mathrm{Are}\:\mathrm{there}\:\mathrm{any}\:\mathrm{other}\:\mathrm{solutions}\:\mathrm{in}\:\mathrm{answer}? \\ $$

Commented by Yozzii last updated on 07/Mar/16

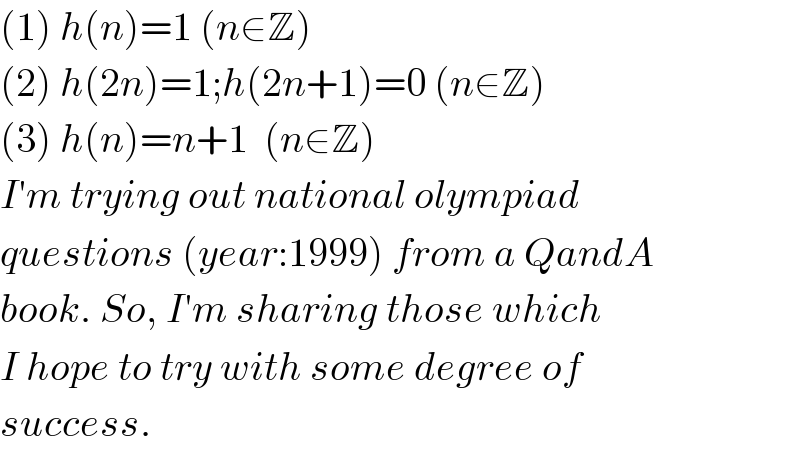
(1) h(n)=1 (n∈Z) (2) h(2n)=1;h(2n+1)=0 (n∈Z) (3) h(n)=n+1 (n∈Z) I′m trying out national olympiad questions (year:1999) from a QandA book. So, I′m sharing those which I hope to try with some degree of success.

$$\left(\mathrm{1}\right)\:{h}\left({n}\right)=\mathrm{1}\:\left({n}\in\mathbb{Z}\right) \\ $$$$\left(\mathrm{2}\right)\:{h}\left(\mathrm{2}{n}\right)=\mathrm{1};{h}\left(\mathrm{2}{n}+\mathrm{1}\right)=\mathrm{0}\:\left({n}\in\mathbb{Z}\right) \\ $$$$\left(\mathrm{3}\right)\:{h}\left({n}\right)={n}+\mathrm{1}\:\:\left({n}\in\mathbb{Z}\right) \\ $$$${I}'{m}\:{trying}\:{out}\:{national}\:{olympiad} \\ $$$${questions}\:\left({year}:\mathrm{1999}\right)\:{from}\:{a}\:{QandA}\: \\ $$$${book}.\:{So},\:{I}'{m}\:{sharing}\:{those}\:{which} \\ $$$${I}\:{hope}\:{to}\:{try}\:{with}\:{some}\:{degree}\:{of}\: \\ $$$${success}. \\ $$

Commented by prakash jain last updated on 07/Mar/16

I will check for mistakes in my arguments. I thin mistake may be in handling the case h(−1)=0

$$\mathrm{I}\:\mathrm{will}\:\mathrm{check}\:\mathrm{for}\:\mathrm{mistakes}\:\mathrm{in}\:\mathrm{my}\:\mathrm{arguments}. \\ $$$$\mathrm{I}\:\mathrm{thin}\:\mathrm{mistake}\:\mathrm{may}\:\mathrm{be}\:\mathrm{in}\:\mathrm{handling}\:\mathrm{the}\:\mathrm{case} \\ $$$${h}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$

Commented by prakash jain last updated on 07/Mar/16

h(0)=1 case h(−1)=0 h(x+y)+h(xy)=h(x)h(y)+1 x=n,y=−1 h(n−1)+h(−n)=h(n)h(−1)+1 h(n−1)=1−h(−n) The above is linear equation solution a: h(n)=an+b a(n−1)+b=1−(−an+b) an−a+b=1+an−b −a+b=1−b⇒b=((1+a)/2) h(n)=an+((1+a)/2) h(−1)=0⇒0=−a+((1+a)/2)⇒a=1 h(n)=n+1 (solution a) h(x+y)+h(xy)=h(x)h(y)+1 x+y+1+(xy+1)=(x+1)(y+1)+1 h(−n−1)=1−h(−n) or h(n−1)=1−h(n) given h(−1)=0,h(0)=1 h(n)=1−h(n−1) h(1)=1−h(0)=0 h(2)=1−h(1)=1 or h(n)= { ((0 n odd)),((1 n even)) :}

$${h}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{case}\:{h}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$${h}\left({x}+{y}\right)+{h}\left({xy}\right)={h}\left({x}\right){h}\left({y}\right)+\mathrm{1} \\ $$$${x}={n},{y}=−\mathrm{1} \\ $$$${h}\left({n}−\mathrm{1}\right)+{h}\left(−{n}\right)={h}\left({n}\right){h}\left(−\mathrm{1}\right)+\mathrm{1} \\ $$$${h}\left({n}−\mathrm{1}\right)=\mathrm{1}−{h}\left(−{n}\right) \\ $$$$\mathrm{The}\:\mathrm{above}\:\mathrm{is}\:\mathrm{linear}\:\mathrm{equation} \\ $$$${solution}\:{a}: \\ $$$${h}\left({n}\right)={an}+{b} \\ $$$${a}\left({n}−\mathrm{1}\right)+{b}=\mathrm{1}−\left(−{an}+{b}\right) \\ $$$${an}−{a}+{b}=\mathrm{1}+{an}−{b} \\ $$$$−{a}+{b}=\mathrm{1}−{b}\Rightarrow{b}=\frac{\mathrm{1}+{a}}{\mathrm{2}} \\ $$$${h}\left({n}\right)={an}+\frac{\mathrm{1}+{a}}{\mathrm{2}} \\ $$$${h}\left(−\mathrm{1}\right)=\mathrm{0}\Rightarrow\mathrm{0}=−{a}+\frac{\mathrm{1}+{a}}{\mathrm{2}}\Rightarrow{a}=\mathrm{1} \\ $$$${h}\left({n}\right)={n}+\mathrm{1}\:\left({solution}\:{a}\right) \\ $$$${h}\left({x}+{y}\right)+{h}\left({xy}\right)={h}\left({x}\right){h}\left({y}\right)+\mathrm{1} \\ $$$${x}+{y}+\mathrm{1}+\left({xy}+\mathrm{1}\right)=\left({x}+\mathrm{1}\right)\left({y}+\mathrm{1}\right)+\mathrm{1} \\ $$$$ \\ $$$${h}\left(−{n}−\mathrm{1}\right)=\mathrm{1}−{h}\left(−{n}\right) \\ $$$$\mathrm{or}\:{h}\left({n}−\mathrm{1}\right)=\mathrm{1}−{h}\left({n}\right)\:\:\mathrm{given}\:{h}\left(−\mathrm{1}\right)=\mathrm{0},{h}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${h}\left({n}\right)=\mathrm{1}−{h}\left({n}−\mathrm{1}\right) \\ $$$${h}\left(\mathrm{1}\right)=\mathrm{1}−{h}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${h}\left(\mathrm{2}\right)=\mathrm{1}−{h}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${or}\:{h}\left({n}\right)=\begin{cases}{\mathrm{0}\:{n}\:{odd}}\\{\mathrm{1}\:{n}\:{even}}\end{cases} \\ $$

Commented by Yozzii last updated on 07/Mar/16

Looks like thats one approach to figuring out the answer. Nice!

$${Looks}\:{like}\:{thats}\:{one}\:{approach}\:{to}\: \\ $$$${figuring}\:{out}\:{the}\:{answer}.\:{Nice}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com