
Question and Answers Forum
Question Number 47566 by tanmay.chaudhury50@gmail.com last updated on 11/Nov/18
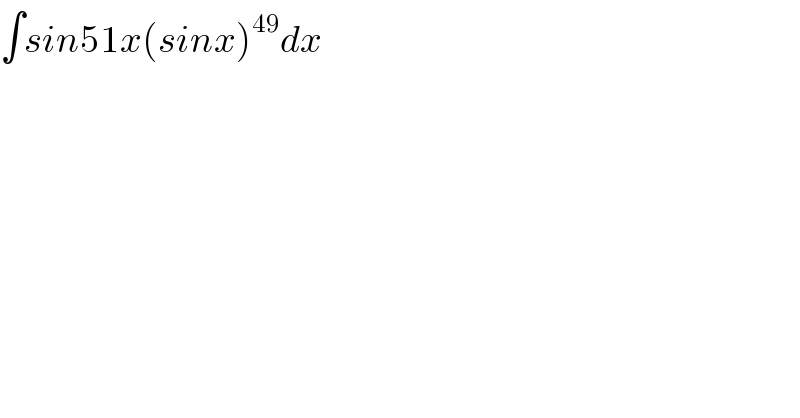
Answered by Smail last updated on 12/Nov/18
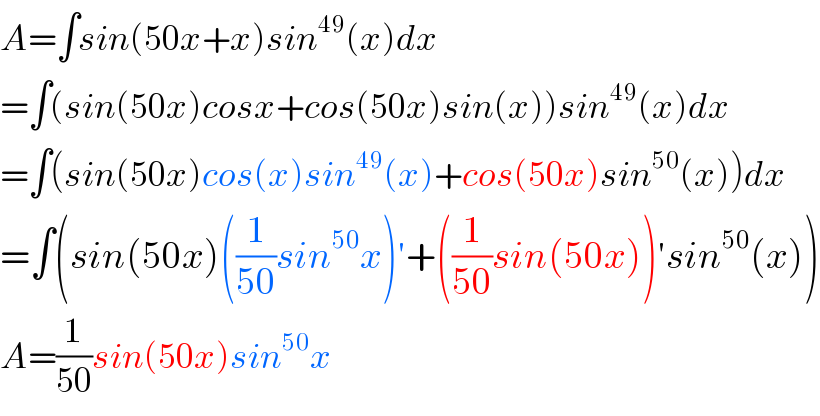
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Nov/18
^(49) dx ∫sin50xcosx(sinx)^(49) +cos50x(sinx)^(50) dx (1/(50))∫sin50x×50cosx(sinx)^(49) +50cos50x(sinx)^(50) dx (1/(50))∫[sin50x×(d/dx){(sinx)^(50) }+(sinx)^(50) ×(d/dx)(sin50x)]dx (1/(50))∫(d/dx){sin50x×(sinx)^(50) }dx (1/(50))×{sin50x×(sinx)^(50) }+c](Q47601.png)
| ||
Question and Answers Forum | ||
Question Number 47566 by tanmay.chaudhury50@gmail.com last updated on 11/Nov/18 | ||
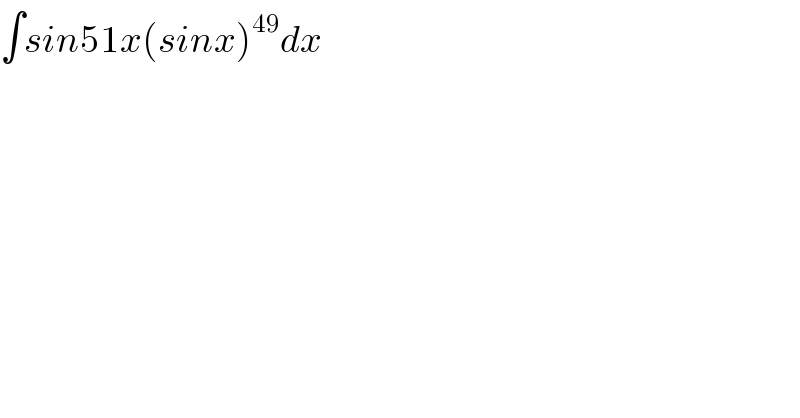 | ||
Answered by Smail last updated on 12/Nov/18 | ||
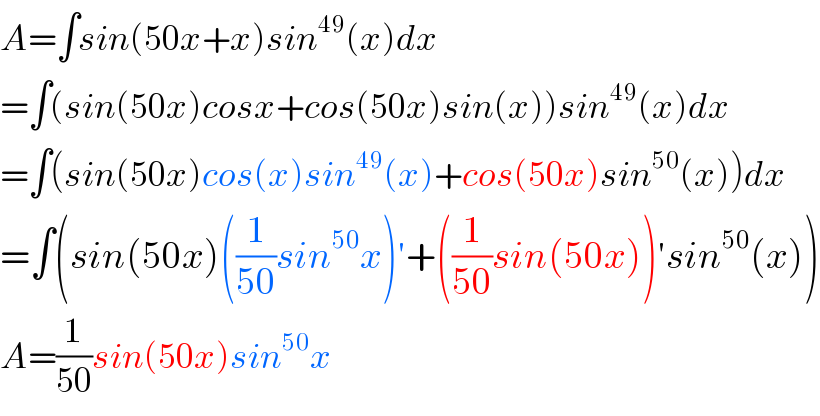 | ||
| ||
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Nov/18 | ||
^(49) dx ∫sin50xcosx(sinx)^(49) +cos50x(sinx)^(50) dx (1/(50))∫sin50x×50cosx(sinx)^(49) +50cos50x(sinx)^(50) dx (1/(50))∫[sin50x×(d/dx){(sinx)^(50) }+(sinx)^(50) ×(d/dx)(sin50x)]dx (1/(50))∫(d/dx){sin50x×(sinx)^(50) }dx (1/(50))×{sin50x×(sinx)^(50) }+c](Q47601.png) | ||
| ||