
Question Number 4758 by madscientist last updated on 05/Mar/16
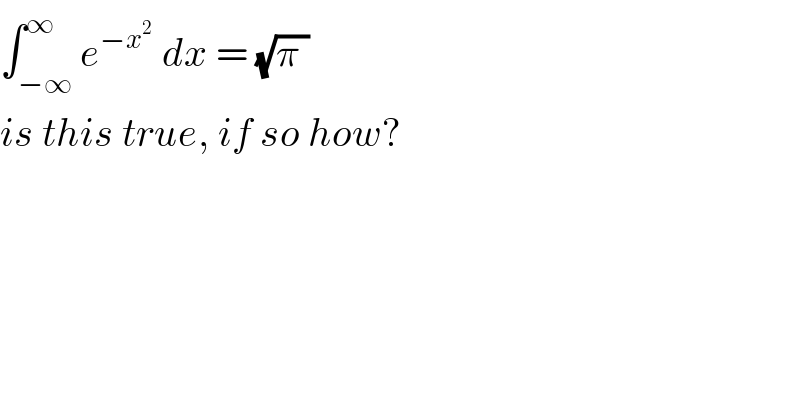
$$\int_{−\infty} ^{\infty} {e}^{−{x}^{\mathrm{2}\:} } \:{dx}\:=\:\sqrt{\pi\:} \\ $$$${is}\:{this}\:{true},\:{if}\:{so}\:{how}? \\ $$
Answered by Yozzii last updated on 05/Mar/16
![Let f(x)=e^(−x^2 ) (x∈R). Since f(−x)=e^(−(−x)^2 ) =e^(−x^2 ) =f(x) then f(x) is an even function. In general, for g(u) being an even function, ∫_(−a) ^a g(u)du=2∫_0 ^a g(u)du if the integral exists wholly on u∈[−a,a]. Now let I(a)=∫_(−a) ^a f(x)dx. Then, I(a)=2∫_0 ^a f(x)dx since f(x) is even. Let us now determine l=lim_(a→∞) I(a)=lim_(a→∞) 2∫_0 ^a f(x)dx.⇒l=2∫_0 ^∞ e^(−x^2 ) dx. Substitute u=x^2 where x≥0.⇒x=(√u). Also, du=2xdx=2(√u)dx⇒(1/2)u^(−1/2) du=dx. At x=0,u=0^2 =0 and as x→∞,x^2 →∞ ⇒u→∞. l hence becomes l=2∫_0 ^∞ 0.5u^(−1/2) e^(−u) du=∫_0 ^∞ u^(−1/2) e^(−u) du. The gamma function Γ is given by the form Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt (x>0). So truly l=Γ(1/2). From the equation for 0<x<1 Γ(x)Γ(1−x)=(π/(sinπx)), let x=1/2. ⇒Γ^2 (0.5)=(π/(sin0.5π))=π⇒Γ(0.5)=±(√π). Since f(x)>0 for all x≥0, the integral ought to be non−negative. Hence, Γ(0.5)=(√π) only.⇒ l=(√π). But l is equivalent to the form ∫_(−∞) ^∞ e^(−x^2 ) dx. So, ∫_(−∞) ^∞ e^(−x^2 ) dx=(√π). The mathematical statement is true.](Q4759.png)
$${Let}\:{f}\left({x}\right)={e}^{−{x}^{\mathrm{2}} } \:\left({x}\in\mathbb{R}\right).\:{Since}\:{f}\left(−{x}\right)={e}^{−\left(−{x}\right)^{\mathrm{2}} } ={e}^{−{x}^{\mathrm{2}} } ={f}\left({x}\right) \\ $$$${then}\:{f}\left({x}\right)\:{is}\:{an}\:{even}\:{function}.\:{In}\:{general}, \\ $$$${for}\:{g}\left({u}\right)\:{being}\:{an}\:{even}\:{function},\:\int_{−{a}} ^{{a}} {g}\left({u}\right){du}=\mathrm{2}\int_{\mathrm{0}} ^{{a}} {g}\left({u}\right){du} \\ $$$${if}\:{the}\:{integral}\:{exists}\:{wholly}\:{on}\:{u}\in\left[−{a},{a}\right]. \\ $$$${Now}\:{let}\:{I}\left({a}\right)=\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}.\:{Then},\:{I}\left({a}\right)=\mathrm{2}\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx} \\ $$$${since}\:{f}\left({x}\right)\:{is}\:{even}.\:{Let}\:{us}\:{now}\:{determine} \\ $$$${l}=\underset{{a}\rightarrow\infty} {\mathrm{lim}}{I}\left({a}\right)=\underset{{a}\rightarrow\infty} {\mathrm{lim}2}\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}.\Rightarrow{l}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}. \\ $$$${Substitute}\:{u}={x}^{\mathrm{2}} \:{where}\:{x}\geqslant\mathrm{0}.\Rightarrow{x}=\sqrt{{u}}. \\ $$$${Also},\:{du}=\mathrm{2}{xdx}=\mathrm{2}\sqrt{{u}}{dx}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}{u}^{−\mathrm{1}/\mathrm{2}} {du}={dx}. \\ $$$${At}\:{x}=\mathrm{0},{u}=\mathrm{0}^{\mathrm{2}} =\mathrm{0}\:{and}\:{as}\:{x}\rightarrow\infty,{x}^{\mathrm{2}} \rightarrow\infty \\ $$$$\Rightarrow{u}\rightarrow\infty.\:{l}\:{hence}\:{becomes}\: \\ $$$${l}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{0}.\mathrm{5}{u}^{−\mathrm{1}/\mathrm{2}} {e}^{−{u}} {du}=\int_{\mathrm{0}} ^{\infty} {u}^{−\mathrm{1}/\mathrm{2}} {e}^{−{u}} {du}. \\ $$$${The}\:{gamma}\:{function}\:\Gamma\:{is}\:{given}\:{by}\:{the} \\ $$$${form}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}\:\left({x}>\mathrm{0}\right).\:{So}\:{truly} \\ $$$${l}=\Gamma\left(\mathrm{1}/\mathrm{2}\right).\:{From}\:{the}\:{equation}\:{for}\:\mathrm{0}<{x}<\mathrm{1} \\ $$$$\Gamma\left({x}\right)\Gamma\left(\mathrm{1}−{x}\right)=\frac{\pi}{{sin}\pi{x}},\:{let}\:{x}=\mathrm{1}/\mathrm{2}. \\ $$$$\Rightarrow\Gamma^{\mathrm{2}} \left(\mathrm{0}.\mathrm{5}\right)=\frac{\pi}{{sin}\mathrm{0}.\mathrm{5}\pi}=\pi\Rightarrow\Gamma\left(\mathrm{0}.\mathrm{5}\right)=\pm\sqrt{\pi}. \\ $$$${Since}\:{f}\left({x}\right)>\mathrm{0}\:{for}\:{all}\:{x}\geqslant\mathrm{0},\:{the}\:{integral} \\ $$$${ought}\:{to}\:{be}\:{non}−{negative}.\:{Hence},\:\Gamma\left(\mathrm{0}.\mathrm{5}\right)=\sqrt{\pi} \\ $$$${only}.\Rightarrow\:{l}=\sqrt{\pi}.\:{But}\:{l}\:{is}\:{equivalent}\:{to}\:{the} \\ $$$${form}\:\int_{−\infty} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}.\:{So},\:\int_{−\infty} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}=\sqrt{\pi}.\: \\ $$$${The}\:{mathematical}\:{statement}\:{is}\:{true}. \\ $$$$ \\ $$$$ \\ $$
