Question and Answers Forum
Question Number 47735 by behi83417@gmail.com last updated on 14/Nov/18

Commented by mr W last updated on 14/Nov/18

Commented by behi83417@gmail.com last updated on 14/Nov/18

Commented by MJS last updated on 14/Nov/18
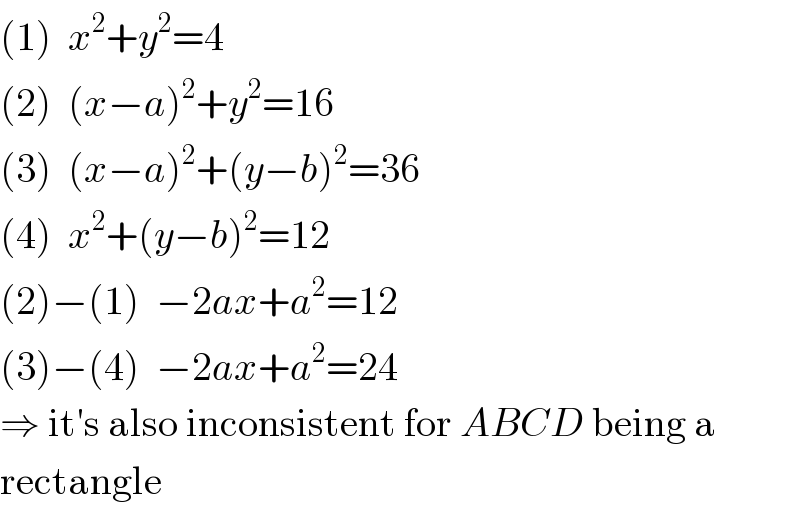
Commented by MJS last updated on 14/Nov/18
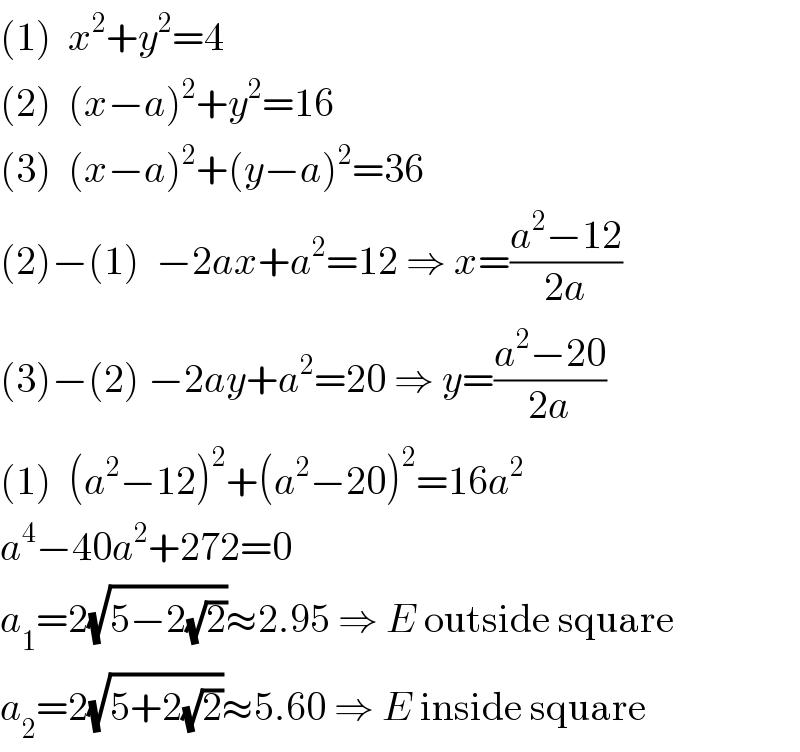
Commented by behi83417@gmail.com last updated on 14/Nov/18

Answered by mr W last updated on 14/Nov/18
![a=distance to vertex A=2 b=distance to vertex B=4 c=distance to vertex C=6 l=side length of square x,y=distance to side BC and AB x^2 +y^2 =b^2 a^2 =(l−x)^2 +y^2 =l^2 −2lx+x^2 +y^2 =l^2 +b^2 −2lx ⇒x=((l^2 +b^2 −a^2 )/(2l)) c^2 =x^2 +(l−y)^2 =x^2 +y^2 +l^2 −2ly=l^2 +b^2 −2ly ⇒y=((l^2 +b^2 −c^2 )/(2l)) (((l^2 +b^2 −a^2 )/(2l)))^2 +(((l^2 +b^2 −c^2 )/(2l)))^2 =b^2 2l^4 +2(2b^2 −a^2 −c^2 )l^2 +[2b^4 +a^4 +c^4 −2(a^2 +c^2 )b^2 ]=4b^2 l^2 2l^4 −2(a^2 +c^2 )l^2 +[2b^4 +a^4 +c^4 −2(a^2 +c^2 )b^2 ]=0 l^2 =(((a^2 +c^2 )±(√((a^4 +c^4 +2a^2 c^2 )−2[2b^4 +a^4 +c^4 −2(a^2 +c^2 )b^2 ])))/2) l^2 =((a^2 +c^2 ±(√([(a+c)^2 −2b^2 ][2b^2 −(a−c)^2 ])))/2) l^2 =((a^2 +c^2 ±(√((a+(√2)b+c)(−a+(√2)b+c)(a−(√2)b+c)(a+(√2)b−c))))/2) l^2 =((2^2 +6^2 ±(√((64−2×16)(2×16−16))))/2) l^2 =20±8(√2) ⇒l=2(√(5±2(√2)))=5.59 or 2.95](Q47760.png)
Commented by behi83417@gmail.com last updated on 14/Nov/18
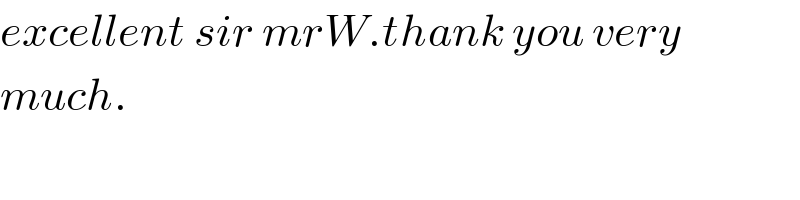
Commented by mr W last updated on 14/Nov/18

Commented by mr W last updated on 14/Nov/18

Commented by behi83417@gmail.com last updated on 14/Nov/18