
Question and Answers Forum
Question Number 47737 by ajfour last updated on 14/Nov/18
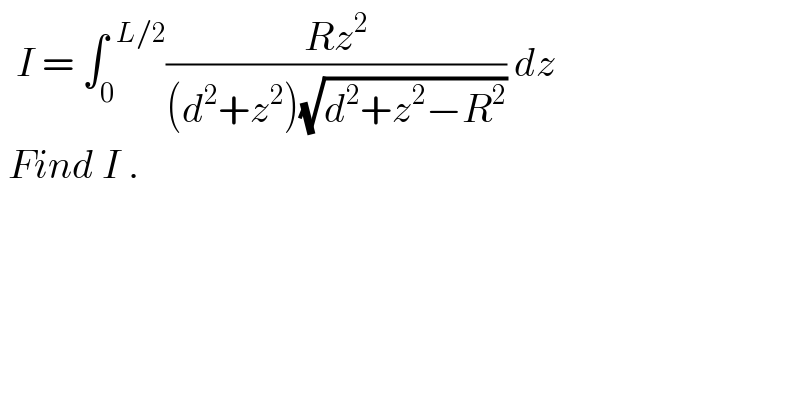
Answered by MJS last updated on 14/Nov/18
![R∫(z^2 /((z^2 +d^2 )(√(z^2 +d^2 −R^2 ))))dz= =R∫(dz/(√(z^2 +d^2 −R^(2 ) )))−d^2 R∫(dz/((z^2 +d^2 )(√(z^2 +d^2 −R^2 )))) R∫(dz/(√(z^2 +d^2 −R^(2 ) )))= [t=(z/(√(d^2 −R^2 ))) → dz=(√(d^2 −R^2 ))dt] =R∫(dt/(√(t^2 +1)))=Rln (t+(√(t^2 +1))) =Rln ((z+(√(z^2 +d^2 −R^2 )))/(√(d^2 −R^2 ))) −d^2 R∫(dz/((z^2 +d^2 )(√(z^2 +d^2 −R^2 ))))= [z=(√(d^2 −R^2 ))tan u → u=arctan (z/(√(d^2 −R^2 ))); dz=(√(d^2 −R^2 ))sec^2 u du] =−d^2 R∫(((√(d^2 −R^2 ))sec^2 u)/((d^2 +(d^2 −R^2 )tan^2 u)(√(d^2 −R^2 +(d^2 −R^2 )tan^2 u))))du= =−d^2 R∫((sec u)/(d^2 +(d^2 −R^2 )tan^2 u))du=−d^2 R∫((cos u)/(d^2 −R^2 sin^2 u))du= [v=sin u → du=(dv/(cos u))] =−d^2 R∫(dv/(d^2 −R^2 v^2 ))=−d^2 R∫(dv/((d+Rv)(d−Rv)))= =(dR/2)∫(dv/(d−Rv))−(dR/2)∫(dv/(d+Rv))= =(d/2)ln ((d−Rv)/(d+Rv)) =(d/2)ln ((d−Rsin u)/(d+Rsin u))= =(d/2)ln ((d−Rsin arctan (z/(√(d^2 −R^2 ))))/(d+Rsin arctan (z/(√(d^2 −R^2 )))))= =(d/2)ln ((d−R(z/(√(z^2 +d^2 −R^2 ))))/(d+R(z/(√(z^2 +d^2 −R^2 ))))) =(d/2)ln ((d(√(z^2 +d^2 −R^2 ))−Rz)/(d(√(z^2 +d^2 −R^2 ))+Rz)) ∫((Rz^2 )/((z^2 +d^2 )(√(z^2 +d^2 −R^2 ))))dz= Rln ∣((z+(√(z^2 +d^2 −R^2 )))/(√(d^2 −R^2 )))∣ +(d/2)ln ∣((Rz−d(√(z^2 +d^2 −R^2 )))/(Rz+d(√(z^2 +d^2 −R^2 ))))∣ +C](Q47751.png)
Commented by MJS last updated on 14/Nov/18
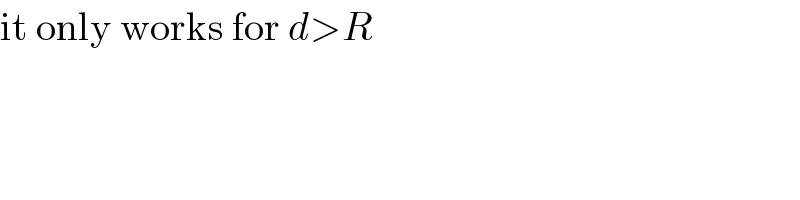
Commented by MJS last updated on 14/Nov/18

Commented by ajfour last updated on 14/Nov/18

Commented by ajfour last updated on 14/Nov/18

