Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 47836 by Aknabob1 last updated on 15/Nov/18

$$prove{cosec}^2\theta -cot\theta cosec\theta =1$$

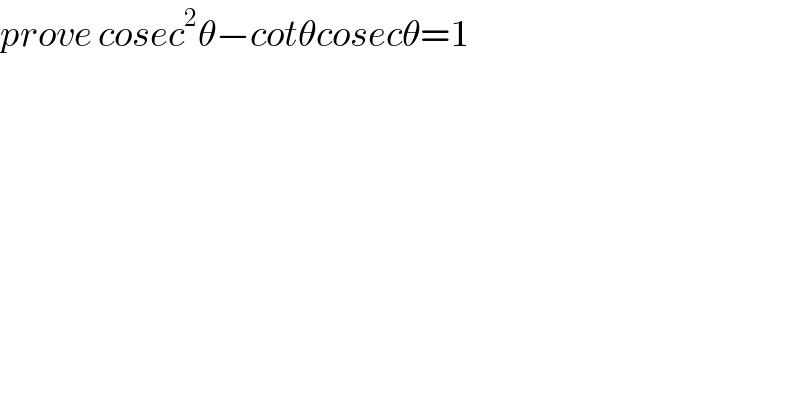
Answered by $@ty@m last updated on 15/Nov/18

$$LHS={cosec}^2\theta -cot\theta cosec\theta$$$$={cosec}^2\theta -\frac{\cos \theta }{\sin \theta }\times \frac{1}{\sin \theta }$$$$=\frac{1}{\sin {}^2\theta }-\frac{\cos \theta }{\sin {}^2\theta }$$$$=\frac{1-\cos \theta }{\sin {}^2\theta }$$$$=\frac{1-\cos \theta }{1-\cos {}^2\theta }$$$$=\frac{1}{1+\cos \theta }$$$$\ne 1$$$$Thequestioniswrong.$$$$Maybetypoerror.$$$$Pl.check$$

Commented by Aknabob1 last updated on 15/Nov/18

$$thanksiappreciate$$

Answered by peter frank last updated on 15/Nov/18

$$\mathrm{cosec}\theta (\mathrm{cosec}\theta -\cot \theta )$$$$\mathrm{cosec}\theta (\frac{1}{\sin \theta }-\frac{\cos \theta }{\sin \theta })$$$$\frac{\mathrm{cosec}\theta }{\sin \theta }(1-\cos \theta )$$$$\frac{1-\cos \theta }{{\sin }^2\theta }=\frac{1-\cos \theta }{1-{\cos }^2\theta }$$$$=\frac{1-\cos \theta }{1+\cos \theta }$$$$\mathrm{hence}{cosec}^2\theta -cot\theta cosec\theta \ne 1$$$$$$

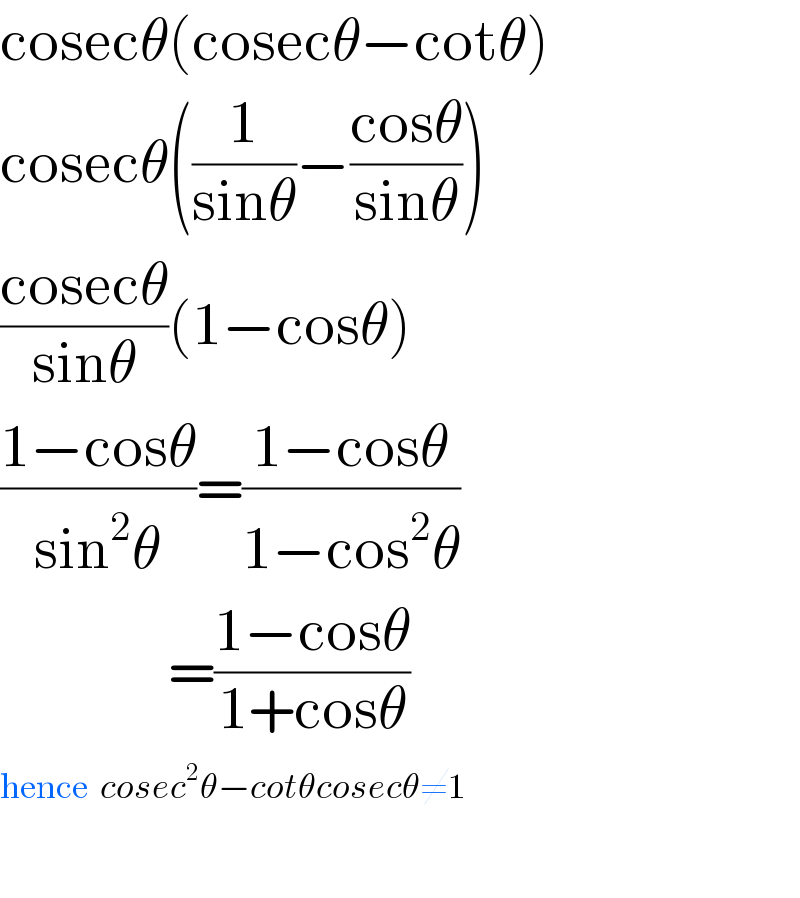
Commented by Aknabob1 last updated on 15/Nov/18

$$thanksiappreciate$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com