calculate A_p =∫_0 ^1 ((x^p −1)/(ln(x)))dx with p>0.


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 47850 by maxmathsup by imad last updated on 15/Nov/18

$c a l c u l a t e A_{p} = \int_{0}^{1} \frac{x^{p} - 1}{l n (x)} d x w i t h p > 0 .$
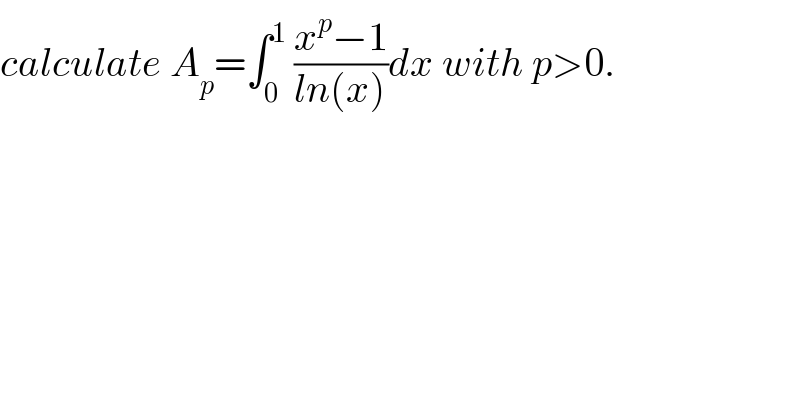
Commented bytanmay.chaudhury50@gmail.com last updated on 16/Nov/18

$i h a v e t r i e d f o l l o w i n g w a y$ $A_{p} = \int_{0}^{1} \frac{x^{p} - 1}{l n x} d x$ $\frac{{d A}_{p}}{d p} = \int_{0}^{1} \frac{\partial}{\partial p} (\frac{x^{p} - 1}{l n x}) d x$ $= \int_{0}^{1} \frac{x^{p} l n x}{l n x} d x$ $= \int_{0}^{1} x^{p} d x$ $=∣ \frac{x^{p + 1}}{p + 1} ∣_{0}^{1} = \frac{1}{p + 1}$ ${d A}_{p} = \frac{d p}{p + 1}$ $\int {d A}_{p} = \int \frac{d p}{p + 1}$ $A_{p} = l n (p + 1) + c$ $n o w i n q u e s t i o n p > 0$ $s o h e r e i s t o p p e d f u r t h e r . . .$ $b u t i f p = 0 a s s u m e d$ $t h e n \int_{0}^{1} \frac{x^{p} - 1}{l n x} d x$ $\int_{0}^{1} \frac{x^{0} - 1}{l n x} d x = 0 = A_{p = 0}$ $t h e n$ $A_{p} = l n (p + 1) + c$ $A_{p = 0} = l n (0 + 1) + c$ $0 = 0 + c$ $c = 0$ $A_{p} = l n (p + 1)$ $s o A_{p} = \int_{0}^{1} \frac{x^{p} - 1}{l n x} d x = l n (p + 1)$ $p l s c h e c k s i r . . .$
Commented bymaxmathsup by imad last updated on 17/Nov/18

$c h a n g e m e n t l n (x) = - t g i v e A_{p} = - \int_{0}^{\infty} \frac{e^{- p t} - 1}{- t} (- e^{- t}) d t$ $= - \int_{0}^{\infty} \frac{e^{- (p + 1) t} - e^{- t}}{t} d t = \int_{0}^{\infty} \frac{e^{- t} - e^{- (p + 1) t}}{t} d t l e t$ $f (p) = \int_{0}^{\infty} \frac{e^{- t} - e^{- (p + 1) t}}{t} d t \Rightarrow f^{^{'}} (p) = \int_{0}^{\infty} \frac{\partial}{\partial p} (\frac{e^{- t} - e^{- t} e^{- p t}}{t}) d t$ $= \int_{0}^{\infty} \frac{- e^{- t} (- t) e^{- p t}}{t} d t = \int_{0}^{\infty} e^{- (p + 1) t} d t = {[- \frac{1}{p + 1} e^{- (p + 1) t}]}_{t = 0}^{\infty}$ $= \frac{1}{p + 1} \Rightarrow f (p) = l n (p + 1) + λ b u t λ = {l i m}_{x \to 0} (f (p) - l n (p + 1)) = 0 \Rightarrow$ $A_{p} = f (p) = l n (p + 1)$ $★ \int_{0}^{1} \frac{x^{p} - 1}{l n (x)} d x = l n (p + 1) ★ w i t h p > 0 .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 16/Nov/18

	$w e k n o w$ $\int_{0}^{1} x^{k} d x =∣ \frac{x^{k + 1}}{k + 1} ∣_{0}^{1} = \frac{1}{k + 1}$ $n o w i n t r e g a t e b o t h s i d e w . r . t k i n t h e i n t e r v a l$ $s a y q t o p$ $\int_{q}^{p} d k [\int_{0}^{1} x^{k} d x] = \int_{q}^{p} \frac{d k}{1 + k}$ $t a k i n g h e l p f r o m a d v a n c e d l e v e l i n t r e g a t i o n$ $\int_{0}^{1} d x \int_{q}^{p} x^{k} d k =∣ l n (1 + k) ∣_{q}^{p}$ $\int_{0}^{1} d x [∣ \frac{x^{k}}{l n x} ∣_{q}^{p}] = l n (\frac{1 + p}{1 + q})$ $\int_{0}^{1} \frac{x^{p} - x^{q}}{l n x} d x = l n (\frac{1 + p}{1 + q}) = l n (1 + p) - l n (1 + q)$ $n o w p u t q = 0 b o t h s i d e$ $\int_{0}^{1} \frac{x^{p} - 1}{l n x} d x = l n (1 + p) a n s$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum