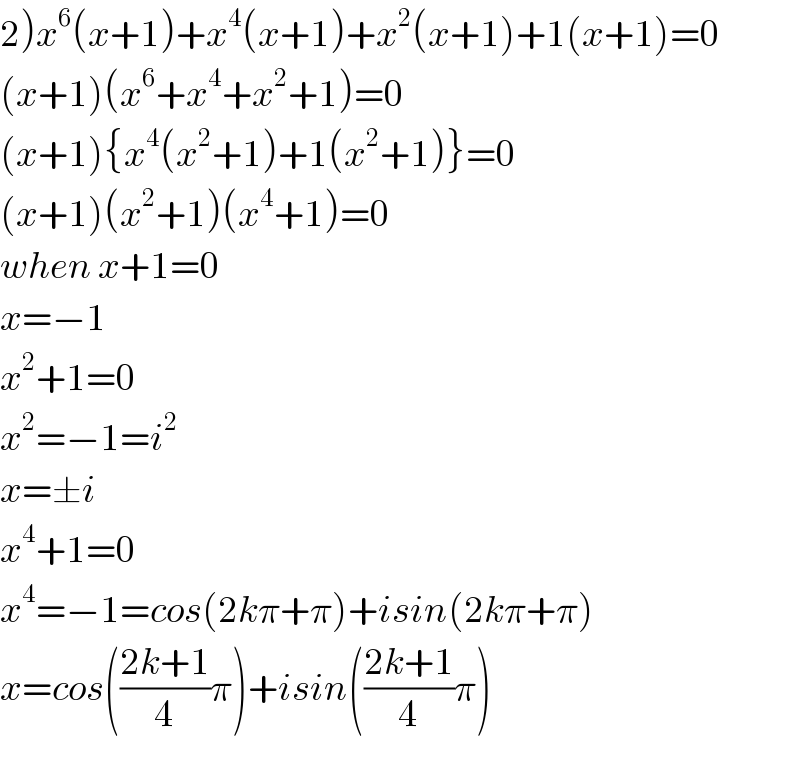Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 47986 by behi83417@gmail.com last updated on 17/Nov/18

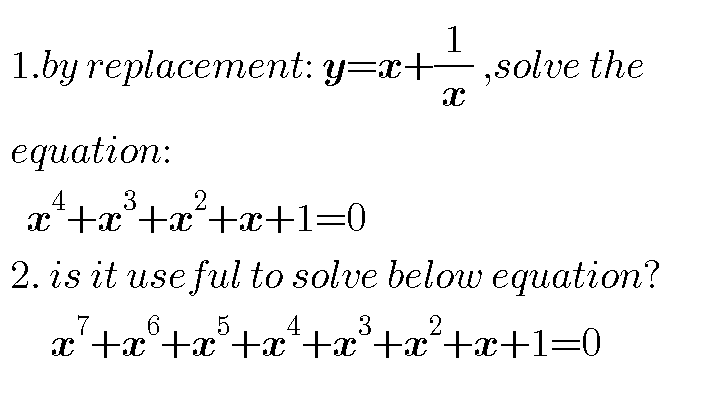
Commented by maxmathsup by imad last updated on 18/Nov/18

2) (e) ⇔ ((1−x^8 )/(1−x)) =0 ⇔ x^8 =1 and x≠1 x=r e^(iθ) ⇒r^8 e^(i8θ) =e^(i2kπ) ⇒ r=1and 8θ=2kπ ⇒ x_k =e^(i((kπ)/4)) with k ∈[[1,7]] are the roots of this equation.

$$\left.\mathrm{2}\right)\:\left({e}\right)\:\Leftrightarrow\:\frac{\mathrm{1}−{x}^{\mathrm{8}} }{\mathrm{1}−{x}}\:=\mathrm{0}\:\:\Leftrightarrow\:{x}^{\mathrm{8}} =\mathrm{1}\:\:\:{and}\:{x}\neq\mathrm{1}\:\:\:{x}={r}\:{e}^{{i}\theta} \:\Rightarrow{r}^{\mathrm{8}} \:{e}^{{i}\mathrm{8}\theta} ={e}^{{i}\mathrm{2}{k}\pi} \:\Rightarrow \\ $$$${r}=\mathrm{1}{and}\:\mathrm{8}\theta=\mathrm{2}{k}\pi\:\Rightarrow\:{x}_{{k}} ={e}^{{i}\frac{{k}\pi}{\mathrm{4}}} \:\:\:{with}\:{k}\:\in\left[\left[\mathrm{1},\mathrm{7}\right]\right]\:{are}\:{the}\:{roots}\:{of}\:{this}\:{equation}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 18/Nov/18

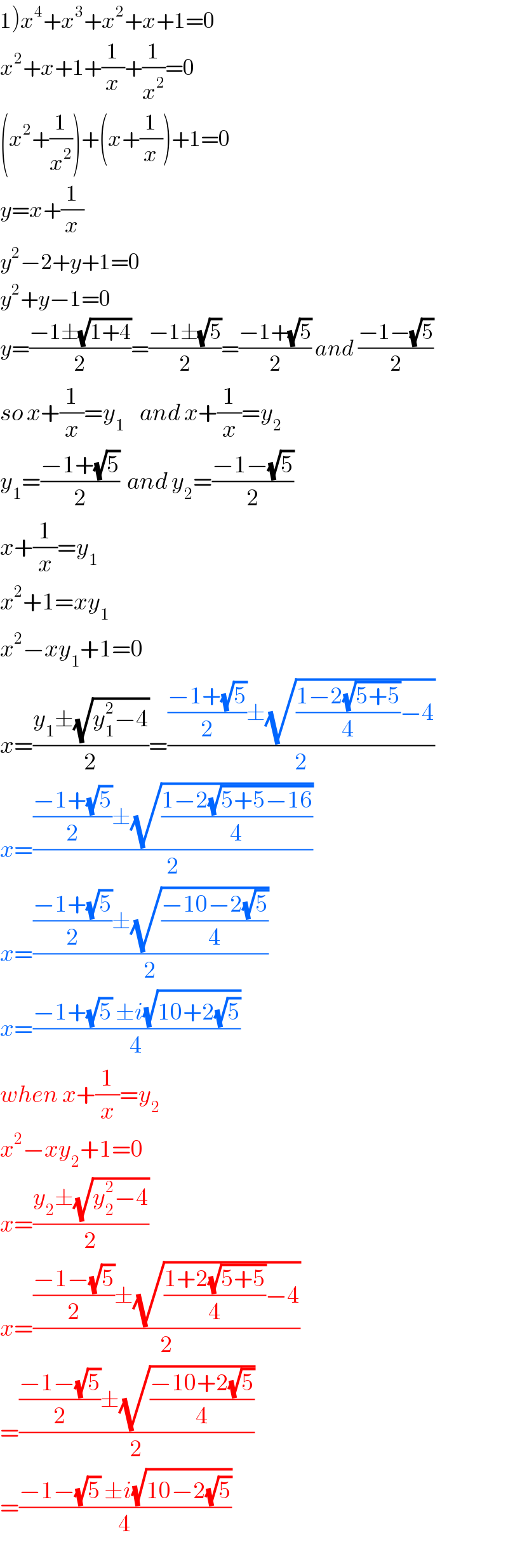
1)x^4 +x^3 +x^2 +x+1=0 x^2 +x+1+(1/x)+(1/x^2 )=0 (x^2 +(1/x^2 ))+(x+(1/x))+1=0 y=x+(1/x) y^2 −2+y+1=0 y^2 +y−1=0 y=((−1±(√(1+4)))/2)=((−1±(√5))/2)=((−1+(√5))/2) and ((−1−(√5))/2) so x+(1/x)=y_1 and x+(1/x)=y_2 y_1 =((−1+(√5))/2) and y_2 =((−1−(√5))/2) x+(1/x)=y_1 x^2 +1=xy_1 x^2 −xy_1 +1=0 x=((y_1 ±(√(y_1 ^2 −4)))/2)=((((−1+(√5))/2)±(√(((1−2(√(5+5)))/4)−4)))/2) x=((((−1+(√5))/2)±(√((1−2(√(5+5−16)))/4)))/2) x=((((−1+(√5))/2)±(√((−10−2(√5))/4)))/2) x=((−1+(√5) ±i(√(10+2(√5))))/4) when x+(1/x)=y_2 x^2 −xy_2 +1=0 x=((y_2 ±(√(y_2 ^2 −4)))/2) x=((((−1−(√5))/2)±(√(((1+2(√(5+5)))/4)−4)))/2) =((((−1−(√5))/2)±(√((−10+2(√5))/4)))/2) =((−1−(√5) ±i(√(10−2(√5))))/4)

$$\left.\mathrm{1}\right){x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{1}=\mathrm{0} \\ $$$${y}={x}+\frac{\mathrm{1}}{{x}} \\ $$$${y}^{\mathrm{2}} −\mathrm{2}+{y}+\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} +{y}−\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:{and}\:\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${so}\:{x}+\frac{\mathrm{1}}{{x}}={y}_{\mathrm{1}} \:\:\:\:{and}\:{x}+\frac{\mathrm{1}}{{x}}={y}_{\mathrm{2}} \:\:\:\: \\ $$$${y}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:{and}\:{y}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}+\frac{\mathrm{1}}{{x}}={y}_{\mathrm{1}} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}={xy}_{\mathrm{1}} \\ $$$${x}^{\mathrm{2}} −{xy}_{\mathrm{1}} +\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{{y}_{\mathrm{1}} \pm\sqrt{{y}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}=\frac{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{5}+\mathrm{5}}}{\mathrm{4}}−\mathrm{4}}}{\mathrm{2}} \\ $$$${x}=\frac{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{5}+\mathrm{5}−\mathrm{16}}}{\mathrm{4}}}}{\mathrm{2}} \\ $$$${x}=\frac{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\sqrt{\frac{−\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}}}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}\:\pm{i}\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$${when}\:{x}+\frac{\mathrm{1}}{{x}}={y}_{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −{xy}_{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{{y}_{\mathrm{2}} \pm\sqrt{{y}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$${x}=\frac{\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}+\mathrm{5}}}{\mathrm{4}}−\mathrm{4}}}{\mathrm{2}} \\ $$$$=\frac{\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\sqrt{\frac{−\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}}}{\mathrm{2}} \\ $$$$=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}\:\pm{i}\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 18/Nov/18

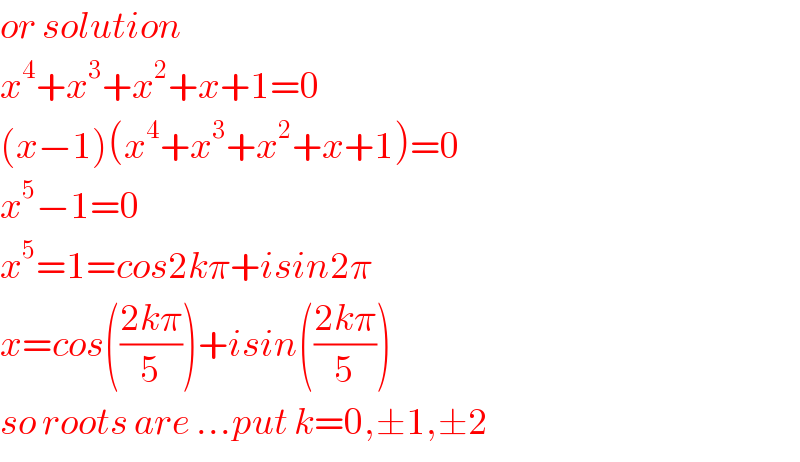
or solution x^4 +x^3 +x^2 +x+1=0 (x−1)(x^4 +x^3 +x^2 +x+1)=0 x^5 −1=0 x^5 =1=cos2kπ+isin2π x=cos(((2kπ)/5))+isin(((2kπ)/5)) so roots are ...put k=0,±1,±2

$${or}\:{solution} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{5}} −\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{5}} =\mathrm{1}={cos}\mathrm{2}{k}\pi+{isin}\mathrm{2}\pi \\ $$$${x}={cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right) \\ $$$${so}\:{roots}\:{are}\:...{put}\:{k}=\mathrm{0},\pm\mathrm{1},\pm\mathrm{2} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 18/Nov/18

2)x^6 (x+1)+x^4 (x+1)+x^2 (x+1)+1(x+1)=0 (x+1)(x^6 +x^4 +x^2 +1)=0 (x+1){x^4 (x^2 +1)+1(x^2 +1)}=0 (x+1)(x^2 +1)(x^4 +1)=0 when x+1=0 x=−1 x^2 +1=0 x^2 =−1=i^2 x=±i x^4 +1=0 x^4 =−1=cos(2kπ+π)+isin(2kπ+π) x=cos(((2k+1)/4)π)+isin(((2k+1)/4)π)

$$\left.\mathrm{2}\right){x}^{\mathrm{6}} \left({x}+\mathrm{1}\right)+{x}^{\mathrm{4}} \left({x}+\mathrm{1}\right)+{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)+\mathrm{1}\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{6}} +{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left\{{x}^{\mathrm{4}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{1}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\right\}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} +\mathrm{1}\right)=\mathrm{0} \\ $$$${when}\:{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=−\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =−\mathrm{1}={i}^{\mathrm{2}} \\ $$$${x}=\pm{i} \\ $$$${x}^{\mathrm{4}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} =−\mathrm{1}={cos}\left(\mathrm{2}{k}\pi+\pi\right)+{isin}\left(\mathrm{2}{k}\pi+\pi\right) \\ $$$${x}={cos}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{4}}\pi\right)+{isin}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{4}}\pi\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com