
Question Number 48042 by maxmathsup by imad last updated on 18/Nov/18
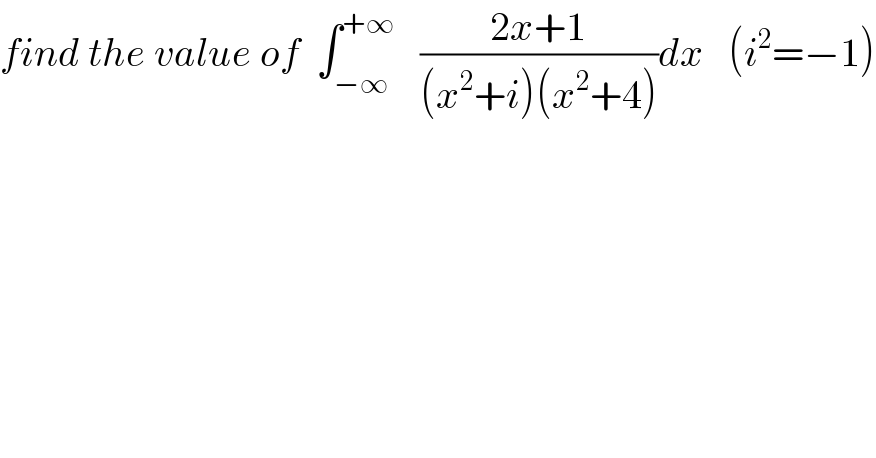
$${find}\:{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +{i}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{dx}\:\:\:\left({i}^{\mathrm{2}} =−\mathrm{1}\right) \\ $$
Commented by maxmathsup by imad last updated on 20/Nov/18

$${let}\:{A}\:=\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +{i}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{dx}\:{and}\:{the}\:{complex}\:{function}\: \\ $$$$\varphi\left({z}\right)\:=\frac{\mathrm{2}{z}+\mathrm{1}}{\left({z}^{\mathrm{2}} +{i}\right)\left({z}^{\mathrm{2}} +\mathrm{4}\right)}\:\Rightarrow\varphi\left({z}\right)=\frac{\mathrm{2}{z}+\mathrm{1}}{\left({z}^{\mathrm{2}} −\left(\sqrt{−{i}}\right)^{\mathrm{2}} \right)\left({z}^{\mathrm{2}} −\left(\mathrm{2}{i}\right)^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}{z}+\mathrm{1}}{\left({z}−\sqrt{−{i}}\right)\left({z}+\sqrt{−{i}}\right)\left({z}−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)}\:=\frac{\mathrm{2}{z}+\mathrm{1}}{\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)} \\ $$$${tbe}\:{ples}\:{of}\:{are}\:\overset{−} {+}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:{and}\:\overset{−} {+}\left(\mathrm{2}{i}\right)\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:+{Res}\left(\varphi,\mathrm{2}{i}\right)\right\} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:+\mathrm{1}}{−\mathrm{2}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \left({e}^{−\frac{{i}\pi}{\mathrm{2}}} \:+\mathrm{4}\right)}\:=\frac{\mathrm{2}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} −\mathrm{1}}{\mathrm{2}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{4}−{i}\right)} \\ $$$${Res}\left(\varphi,\mathrm{2}{i}\right)\:=\frac{\mathrm{4}{i}\:+\mathrm{1}}{\left(\mathrm{4}{i}\right)\left(\left(\mathrm{2}{i}\right)^{\mathrm{2}} +{i}\right)}\:=\frac{\mathrm{4}{i}+\mathrm{1}}{\mathrm{4}{i}\left\{−\mathrm{4}+{i}\right\}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\frac{\mathrm{2}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} −\mathrm{1}}{\mathrm{2}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{4}−{i}\right)}\:+\frac{\mathrm{4}{i}+\mathrm{1}}{\mathrm{4}{i}\left(−\mathrm{4}+{i}\right)}\right\}\:={A}\:. \\ $$
