calculate A =∫_0 ^1 (1+x^2 )(√(1−x^2 ))dx −∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 48064 by maxmathsup by imad last updated on 18/Nov/18

$c a l c u l a t e A = \int_{0}^{1} (1 + x^{2}) \sqrt{1 - x^{2}} d x - \int_{0}^{1} (1 - x^{2}) \sqrt{1 + x^{2}} d x$
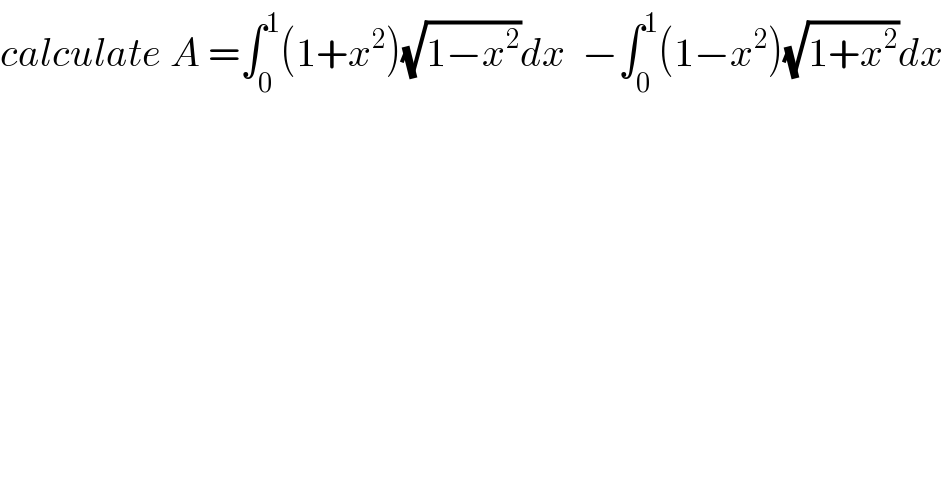
Commented by maxmathsup by imad last updated on 20/Nov/18
$we have A =H−K H=∫_0 ^1 (1+x^2 )(√(1−x^2 ))dx =_(x=sint) ∫_0 ^(π/2) (1+sin^2 t)cost costdt =∫_0 ^(π/2) cos^2 t dt +∫_0 ^(π/2) cos^2 t sin^2 tdt =(1/2)∫_0 ^(π/2) (1+cos(2t))dt +(1/4) ∫_0 ^(π/2) sin^2 (2t)dt =(π/4) +(1/4)[sin(2t)]_0 ^(π/2) +(1/8) ∫_0 ^(π/2) (1−cos(4t))dt =(π/4) +0 +(π/(16)) −(1/(32)) ∫_0 ^(π/2) cos(4t)dt=((5π)/(16)) −(1/(4.32))[sin(4t)]_0 ^(π/2) =((5π)/(16)) let calculate K=∫_0 ^1 (1−x^2 )(√(1+x^2 ))dx ⇒ K =_(x=sh(t) ) ∫_0 ^(argsh(1)) (1−sh^2 t)ch(t)ch(t)dt = ∫_0 ^(ln(1+(√2))) (1−sh^2 t)ch^2 t dt =∫_0 ^(ln(1+(√2))) (1−((ch(2t)−1)/2))(((1+ch(2t))/2))dt =(1/4)∫_0 ^(ln(1+(√2))) (3−ch(2t))(1+ch(2t))dt =(1/4) ∫_0 ^(ln(1+(√2))) {3+3ch(2t)−ch(2t)−ch^2 (2t)}dt =(1/4) ∫_0 ^(ln(1+(√2))) {3 +2ch(2t) −((1+ch(4t))/2)}dt =(3/4)ln(1+(√2)) +(1/2) ∫_0 ^(ln(1+(√2))) ch(2t)dt −(1/8)ln(1+(√2))−(1/8) ∫_0 ^(ln(1+(√2))) ch(4t)dt =(5/8)ln(1+(√2)) +(1/4)[sh(2t)]_0 ^(ln(1+(√2))) −(1/(32))[sh(4t)]_0 ^(ln(1+(√2))) =(5/8)ln(1+(√2))+(1/4)[((e^(2t) −e^(−2t) )/2)]_0 ^(ln(1+(√2))) −(1/(32))[((e^(4t) −e^(−4t) )/2)]_0 ^(ln(1+(√2))) K=(5/8)ln(1+(√2)) +(1/8)( (1+(√2))^2 −(1/((1+(√2))^2 )))−(1/(64))( (1+(√2))^4 −(1/((1+(√2))^4 ))) A=((5π)/(16)) −K so the value of A is known.$
$w e h a v e A = H - K$ $H = \int_{0}^{1} (1 + x^{2}) \sqrt{1 - x^{2}} d x =_{x = s i n t} \int_{0}^{\frac{π}{2}} (1 + {s i n}^{2} t) c o s t c o s t d t$ $= \int_{0}^{\frac{π}{2}} {c o s}^{2} t d t + \int_{0}^{\frac{π}{2}} {c o s}^{2} t {s i n}^{2} t d t$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} (1 + c o s (2 t)) d t + \frac{1}{4} \int_{0}^{\frac{π}{2}} {s i n}^{2} (2 t) d t$ $= \frac{π}{4} + \frac{1}{4} {[s i n (2 t)]}_{0}^{\frac{π}{2}} + \frac{1}{8} \int_{0}^{\frac{π}{2}} (1 - c o s (4 t)) d t$ $= \frac{π}{4} + 0 + \frac{π}{16} - \frac{1}{32} \int_{0}^{\frac{π}{2}} c o s (4 t) d t = \frac{5 π}{16} - \frac{1}{4.32} {[s i n (4 t)]}_{0}^{\frac{π}{2}}$ $= \frac{5 π}{16} l e t c a l c u l a t e K = \int_{0}^{1} (1 - x^{2}) \sqrt{1 + x^{2}} d x \Rightarrow$ $K =_{x = s h (t)} \int_{0}^{a r g s h (1)} (1 - {s h}^{2} t) c h (t) c h (t) d t$ $= \int_{0}^{l n (1 + \sqrt{2})} (1 - {s h}^{2} t) {c h}^{2} t d t = \int_{0}^{l n (1 + \sqrt{2})} (1 - \frac{c h (2 t) - 1}{2}) (\frac{1 + c h (2 t)}{2}) d t$ $= \frac{1}{4} \int_{0}^{l n (1 + \sqrt{2})} (3 - c h (2 t)) (1 + c h (2 t)) d t$ $= \frac{1}{4} \int_{0}^{l n (1 + \sqrt{2})} {3 + 3 c h (2 t) - c h (2 t) - {c h}^{2} (2 t)} d t$ $= \frac{1}{4} \int_{0}^{l n (1 + \sqrt{2})} {3 + 2 c h (2 t) - \frac{1 + c h (4 t)}{2}} d t$ $= \frac{3}{4} l n (1 + \sqrt{2}) + \frac{1}{2} \int_{0}^{l n (1 + \sqrt{2})} c h (2 t) d t - \frac{1}{8} l n (1 + \sqrt{2}) - \frac{1}{8} \int_{0}^{l n (1 + \sqrt{2})} c h (4 t) d t$ $= \frac{5}{8} l n (1 + \sqrt{2}) + \frac{1}{4} {[s h (2 t)]}_{0}^{l n (1 + \sqrt{2})} - \frac{1}{32} {[s h (4 t)]}_{0}^{l n (1 + \sqrt{2})}$ $= \frac{5}{8} l n (1 + \sqrt{2}) + \frac{1}{4} {[\frac{e^{2 t} - e^{- 2 t}}{2}]}_{0}^{l n (1 + \sqrt{2})} - \frac{1}{32} {[\frac{e^{4 t} - e^{- 4 t}}{2}]}_{0}^{l n (1 + \sqrt{2})}$ $K = \frac{5}{8} l n (1 + \sqrt{2}) + \frac{1}{8} ({(1 + \sqrt{2})}^{2} - \frac{1}{{(1 + \sqrt{2})}^{2}}) - \frac{1}{64} ({(1 + \sqrt{2})}^{4} - \frac{1}{{(1 + \sqrt{2})}^{4}})$ $A = \frac{5 π}{16} - K s o t h e v a l u e o f A i s k n o w n .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

	$= \int_{0}^{1} \sqrt{1 - x^{2}} + x^{2} \sqrt{1 - x^{2}} - \sqrt{1 + x^{2}} + x^{2} \sqrt{1 + x^{2}} d x$ $I_{1} = \int_{0}^{1} \sqrt{1 - x^{2}} d x$ $I_{2} = \int_{0}^{1} \sqrt{1 + x^{2}} d x$ $I_{3} = \int_{0}^{1} x^{2} \sqrt{1 - x^{2}} d x$ $I_{4} = \int_{0}^{1} x^{2} \sqrt{1 + x^{2}} d x$ $I = I_{1} - I_{2} + I_{3} + I_{4}$ $u s e f o r m u l a s a t t a c h i n g h e r e w i t h t l s o l v e . . .$
	Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

	Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum