∫_(−1) ^1 ((√(1+x+x^2 ))− (√(1−x−x^2 )) )dx =


Question and Answers Forum

All Questions Topic List
UNKNOWN Questions
Previous in All Question Next in All Question
Previous in UNKNOWN Next in UNKNOWN
Question Number 48105 by lhfgfgjokf last updated on 19/Nov/18

$\underset{- 1}{\int^{1}} (\sqrt{1 + x + x^{2}} - \sqrt{1 - x - x^{2}}) d x =$
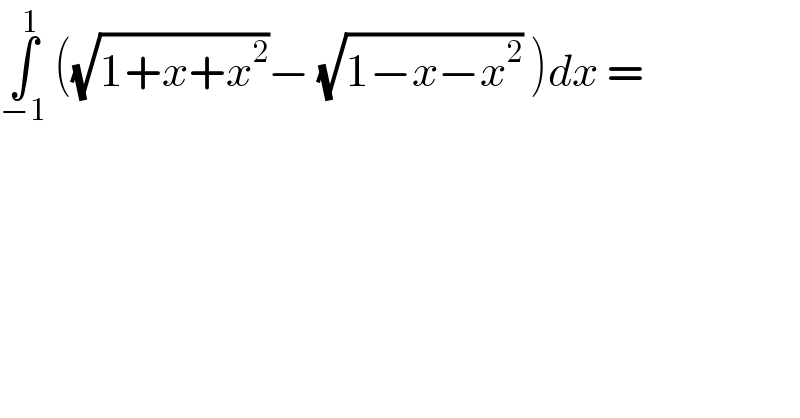
Commented by maxmathsup by imad last updated on 19/Nov/18
$I =H−K with H =∫_(−1) ^1 (√(x^2 +x+1))dx H = ∫_(−1) ^1 (√((x+(1/2))^2 +(3/4)))dx =_(x+(1/2)=((√3)/2)sh(t)) ∫_(−argsh((1/(√3)))) ^(argsh((√3))) ((√3)/2) ch(t)((√3)/2)ch(t)dt =(3/4) ∫_(−ln((1/(√3))+(2/(√3)))) ^(ln((√3)+2)) ((1+ch(2t))/2) dt =(3/8){ln((√3)+2)+ln((√3))} +(3/(16))[sh(2t)]_(−ln((√3))) ^(ln(2+(√3))) =(3/8){ln(2+(√3))+ln((√3))}+(3/(32)){e^(2t) −e^(−2t) ]_(−ln((√3))) ^(ln(2+(√3))) =(3/8){ln(2+(√3)) +ln((√3))}+(3/(32)){(2+(√3))^2 −(1/((2+(√3))^2 )) −( (1/(((√3))^2 )) +((√3))^2 )}$
$I = H - K w i t h H = \int_{- 1}^{1} \sqrt{x^{2} + x + 1} d x$ $H = \int_{- 1}^{1} \sqrt{{(x + \frac{1}{2})}^{2} + \frac{3}{4}} d x =_{x + \frac{1}{2} = \frac{\sqrt{3}}{2} s h (t)} \int_{- a r g s h (\frac{1}{\sqrt{3}})}^{a r g s h (\sqrt{3})} \frac{\sqrt{3}}{2} c h (t) \frac{\sqrt{3}}{2} c h (t) d t$ $= \frac{3}{4} \int_{- l n (\frac{1}{\sqrt{3}} + \frac{2}{\sqrt{3}})}^{l n (\sqrt{3} + 2)} \frac{1 + c h (2 t)}{2} d t = \frac{3}{8} {l n (\sqrt{3} + 2) + l n (\sqrt{3})}$ $+ \frac{3}{16} {[s h (2 t)]}_{- l n (\sqrt{3})}^{l n (2 + \sqrt{3})} = \frac{3}{8} {l n (2 + \sqrt{3}) + l n (\sqrt{3})} + \frac{3}{32} {{e^{2 t} - e^{- 2 t}]}_{- l n (\sqrt{3})}^{l n (2 + \sqrt{3})}$ $= \frac{3}{8} {l n (2 + \sqrt{3}) + l n (\sqrt{3})} + \frac{3}{32} {{(2 + \sqrt{3})}^{2} - \frac{1}{{(2 + \sqrt{3})}^{2}} - (\frac{1}{{(\sqrt{3})}^{2}} + {(\sqrt{3})}^{2})}$
Commented by maxmathsup by imad last updated on 19/Nov/18
$let calculate K =∫_(−1) ^1 (√(−x^2 −x +1)) K =∫_(−1) ^1 (√(1−(x^2 +x)))dx =∫_(−1) ^1 (√(1−((x+(1/2))^2 −(1/4))))dx =∫_(−1) ^1 (√((5/4)−(x+(1/2))^2 ))dx=_(x+(1/2)=((√5)/2)sint) ∫_(−arcsin((1/(√5)))) ^(arcsin((3/(√5)))) ((√5)/2) cost ((√5)/2) cost dt =(5/4) ∫_(−arcsin((1/(√5)))) ^(arcsin((3/(√5)))) cos^2 t dt =(5/8) ∫_(−arcsin((1/(√5)))) ^(arcsin((3/((√5) )))) (1+cos(2t))dt =(5/8){arcsin((3/(√5)))+arcsin((1/(√5)))}+(5/(16))[sin(2t)]_(−arcsin((1/((√5)))))) ^(arcsin((3/((√5) )))) =(5/8){arcsin((3/(√5)))+arcsin((1/(√5))) +(5/(16)){sin(2arcsin((3/(√5)))+sin(2arcsin((1/(√5)))} so the value of I is known .$
$l e t c a l c u l a t e K = \int_{- 1}^{1} \sqrt{- x^{2} - x + 1}$ $K = \int_{- 1}^{1} \sqrt{1 - (x^{2} + x)} d x = \int_{- 1}^{1} \sqrt{1 - ({(x + \frac{1}{2})}^{2} - \frac{1}{4})} d x$ $= \int_{- 1}^{1} \sqrt{\frac{5}{4} - {(x + \frac{1}{2})}^{2}} d x =_{x + \frac{1}{2} = \frac{\sqrt{5}}{2} s i n t} \int_{- a r c s i n (\frac{1}{\sqrt{5}})}^{a r c s i n (\frac{3}{\sqrt{5}})} \frac{\sqrt{5}}{2} c o s t \frac{\sqrt{5}}{2} c o s t d t$ $= \frac{5}{4} \int_{- a r c s i n (\frac{1}{\sqrt{5}})}^{a r c s i n (\frac{3}{\sqrt{5}})} {c o s}^{2} t d t = \frac{5}{8} \int_{- a r c s i n (\frac{1}{\sqrt{5}})}^{a r c s i n (\frac{3}{\sqrt{5}})} (1 + c o s (2 t)) d t$ $= \frac{5}{8} {a r c s i n (\frac{3}{\sqrt{5}}) + a r c s i n (\frac{1}{\sqrt{5}})} + \frac{5}{16} {[s i n (2 t)]}_{- a r c s i n (\frac{1}{\sqrt{5})})}^{a r c s i n (\frac{3}{\sqrt{5}})}$ $= \frac{5}{8} {a r c s i n (\frac{3}{\sqrt{5}}) + a r c s i n (\frac{1}{\sqrt{5}}) + \frac{5}{16} {s i n (2 a r c s i n (\frac{3}{\sqrt{5}}) + s i n (2 a r c s i n (\frac{1}{\sqrt{5}})}$ $s o t h e v a l u e o f I i s k n o w n .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18
	$1+x+x^2 x^2 +2.x.(1/2)+(1/4)+(3/4) (x+(1/2))^2 +(((√3)/2))^2 1−x−x^2 1−(x^2 +2.x.(1/2)+(1/4)−(1/4)) 1+(1/4)−(x+(1/2))^2 =(((√5)/2))^2 −(x+(1/2))^2 formula ∫(√(a^2 +x^2 )) = ((x(√(x^2 +a^2 )) )/2)+(a^2 /2)ln(x+(√(x^2 +a^2 )) ) formula ∫(√(a^2 −x^2 )) dx= ((x(√(a^2 −x^2 )) )/2)+(a^2 /2)sin^(−1) ((x/a)) so first intregal is ∫_(−1) ^1 (√((x+(1/2))^2 +(((√3)/2))^2 )) ∣(((x+(1/2))(√((x+(1/2))^2 +(((√3)/2))^2 )))/2)+(((((√3)/2))^2 )/2)ln{(x+(1/2))+(√((x+(1/2))^2 +(((√3)/2))^2 )) ∣_(−1) ^1 [{(((1+(1/2))(√((9/4)+(3/4))) )/2)+(3/8)ln{((3/2))+(√3) }−{(((((−1)/2))(√((1/4)+(3/4))))/2)+(3/8)ln∣((−1)/2)+1∣}] =((((3/2))(√3))/2)+(3/8)ln{((3/2))+(√3) +(1/4)−(3/8)ln((1/2)) =((3(√3) +1)/4)+(3/8)ln3←value of first intregal calculation of second intregal ∫_(−1) ^1 (√((((√5)/2))^2 −(x+(1/2))^2 )) dx =∣(((x+(1/2))(√((((√5)/2))^2 −(x+(1/2))^2 )))/2)+(((((√5)/2))^2 )/2)sin^(−1) ((((x+(1/2)))/((√5)/2)))∣_(−1) ^1 =[{((((3/2))(√((5/4)−(9/4))) )/2)+(5/8)sin^(−1) ((3/(√5)))}−{(((−(1/2))(√((5/4)−(1/4))))/2)+(5/8)sin^(−1) (((−1)/(√5)))}] =[{((3i)/4)+(5/8)sin^(−1) ((3/(√5)))}−{((−1)/4)+(5/8)sin^(−1) (((−1)/(√5)))}] =((1+3i)/4)+(5/8){sin^(−1) ((3/(√5)))+sin^(−1) ((1/(√5)))} i=complex is coming so pls check the stdps required answer is [{((3(√3) +1)/4)+(3/8)ln3}−{((1+3i)/4)+(5/8){sin^(−1) ((3/(√5)))+sin^(−1) ((1/(√5)))}]$
	$1 + x + x^{2}$ $x^{2} + 2 . x . \frac{1}{2} + \frac{1}{4} + \frac{3}{4}$ ${(x + \frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}$ $1 - x - x^{2}$ $1 - (x^{2} + 2 . x . \frac{1}{2} + \frac{1}{4} - \frac{1}{4})$ $1 + \frac{1}{4} - {(x + \frac{1}{2})}^{2} = {(\frac{\sqrt{5}}{2})}^{2} - {(x + \frac{1}{2})}^{2}$ $f o r m u l a \int \sqrt{a^{2} + x^{2}} =$ $\frac{x \sqrt{x^{2} + a^{2}}}{2} + \frac{a^{2}}{2} l n (x + \sqrt{x^{2} + a^{2}})$ $f o r m u l a \int \sqrt{a^{2} - x^{2}} d x =$ $\frac{x \sqrt{a^{2} - x^{2}}}{2} + \frac{a^{2}}{2} {s i n}^{- 1} (\frac{x}{a})$ $s o f i r s t i n t r e g a l i s \int_{- 1}^{1} \sqrt{{(x + \frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}}$ $∣ \frac{(x + \frac{1}{2}) \sqrt{{(x + \frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}}}{2} + \frac{{(\frac{\sqrt{3}}{2})}^{2}}{2} l n {(x + \frac{1}{2}) + \sqrt{{(x + \frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}} ∣_{- 1}^{1}$ $[{\frac{(1 + \frac{1}{2}) \sqrt{\frac{9}{4} + \frac{3}{4}}}{2} + \frac{3}{8} l n {(\frac{3}{2}) + \sqrt{3}} - {\frac{(\frac{- 1}{2}) \sqrt{\frac{1}{4} + \frac{3}{4}}}{2} + \frac{3}{8} l n ∣ \frac{- 1}{2} + 1 ∣}]$ $= \frac{(\frac{3}{2}) \sqrt{3}}{2} + \frac{3}{8} l n {(\frac{3}{2}) + \sqrt{3} + \frac{1}{4} - \frac{3}{8} l n (\frac{1}{2})$ $= \frac{3 \sqrt{3} + 1}{4} + \frac{3}{8} l n 3 \leftarrow v a l u e o f f i r s t i n t r e g a l$ $c a l c u l a t i o n o f s e c o n d i n t r e g a l$ $\int_{- 1}^{1} \sqrt{{(\frac{\sqrt{5}}{2})}^{2} - {(x + \frac{1}{2})}^{2}} d x$ $=∣ \frac{(x + \frac{1}{2}) \sqrt{{(\frac{\sqrt{5}}{2})}^{2} - {(x + \frac{1}{2})}^{2}}}{2} + \frac{{(\frac{\sqrt{5}}{2})}^{2}}{2} {s i n}^{- 1} (\frac{(x + \frac{1}{2})}{\frac{\sqrt{5}}{2}}) ∣_{- 1}^{1}$ $= [{\frac{(\frac{3}{2}) \sqrt{\frac{5}{4} - \frac{9}{4}}}{2} + \frac{5}{8} {s i n}^{- 1} (\frac{3}{\sqrt{5}})} - {\frac{(- \frac{1}{2}) \sqrt{\frac{5}{4} - \frac{1}{4}}}{2} + \frac{5}{8} {s i n}^{- 1} (\frac{- 1}{\sqrt{5}})}]$ $= [{\frac{3 i}{4} + \frac{5}{8} {s i n}^{- 1} (\frac{3}{\sqrt{5}})} - {\frac{- 1}{4} + \frac{5}{8} {s i n}^{- 1} (\frac{- 1}{\sqrt{5}})}]$ $= \frac{1 + 3 i}{4} + \frac{5}{8} {{s i n}^{- 1} (\frac{3}{\sqrt{5}}) + {s i n}^{- 1} (\frac{1}{\sqrt{5}})}$ $i = c o m p l e x i s c o m i n g s o p l s c h e c k t h e s t d p s$ $r e q u i r e d a n s w e r i s$ $[{\frac{3 \sqrt{3} + 1}{4} + \frac{3}{8} l n 3} - {\frac{1 + 3 i}{4} + \frac{5}{8} {{s i n}^{- 1} (\frac{3}{\sqrt{5}}) + {s i n}^{- 1} (\frac{1}{\sqrt{5}})}]$
	Commented by maxmathsup by imad last updated on 19/Nov/18

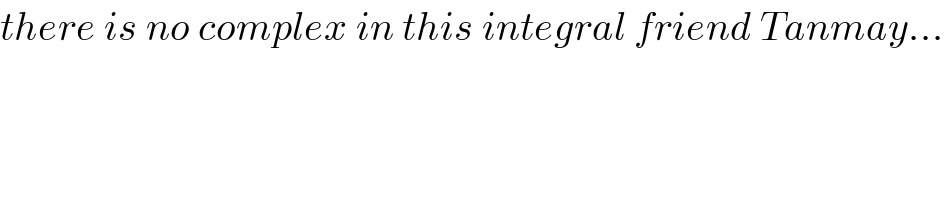
	$t h e r e i s n o c o m p l e x i n t h i s i n t e g r a l f r i e n d T a n m a y . . .$
	Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

	$\sqrt{\frac{5}{4} - \frac{9}{4}}$ $= \sqrt{- 1} i s c o m i n g s o p l s c h e c k . .$
	Commented by MJS last updated on 19/Nov/18

	$I get complex part too .$ $\sqrt{1 - x - x^{2}} \in R \Rightarrow - \frac{1 + \sqrt{3}}{2} ⩽ x ⩽ - \frac{1 - \sqrt{3}}{2} \approx$ $\approx - 1.366 ⩽ x ⩽ . 366$
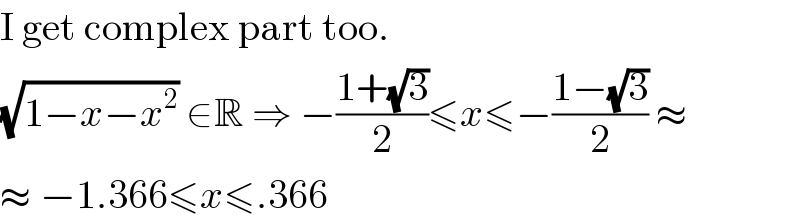
	Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

	$t h a n k y o u s i r . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum