Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 48173 by Abdo msup. last updated on 20/Nov/18

$$calculate\int \frac{arctan\left(x\right)}{\sqrt{1+x^2}}dx$$

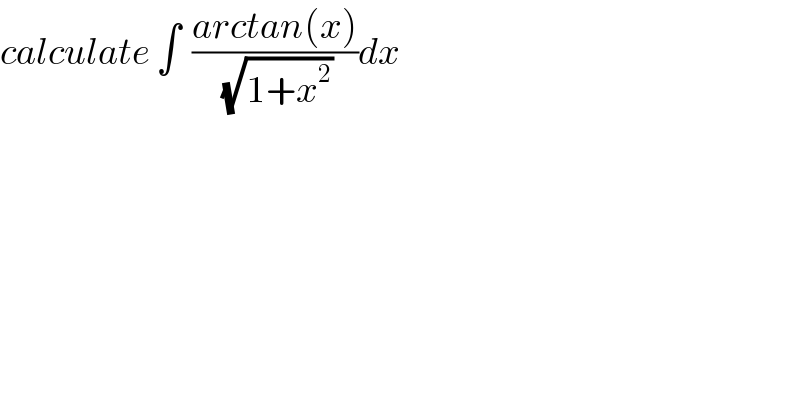
Commented by maxmathsup by imad last updated on 26/Nov/18

$$changementx=tantgiveI=\int \frac{t}{\sqrt{1+{tan}^{2}t}}(1+{tan}^{2}t)d\theta$$$$=\int \theta t\sqrt{1+{tan}^{2}t}dt=\int \frac{t}{cost}dtchangementtan\left(\frac{t}{2}\right)=ugive$$$$I=\int \frac{2arctan\left(u\right)}{\frac{1-u^2}{1+u^2}}\frac{2du}{1+u^2}=4\int \frac{arctan\left(u\right)}{1-u^2}dulet$$$$f\left(\alpha \right)=\int \frac{arctan\left(\alpha u\right)}{1-u^2}du\Rightarrow f^{{}^{\prime }}\left(\alpha \right)=\int \frac{u}{(1-u^2)(1+{\alpha }^2{u}^2)}du$$$${=}_{\alpha u=x}\int \frac{x}{\alpha (1-\frac{x^2}{{\alpha }^2})(1+x^2)}\frac{dx}{\alpha }=\int \frac{xdx}{({\alpha }^2-x^2)(1+x^2)}letdecompose$$$$F\left(x\right)=\frac{-x}{(x^2-{\alpha }^2)(x^2+1)}\Rightarrow F\left(x\right)=\frac{a}{x-\alpha }+\frac{b}{x+\alpha }+\frac{cx+d}{x^2+1}wehave$$$$F\left(x\right)=\frac{-x}{(x-\alpha )(x+\alpha )(x^2+1)}\Rightarrow a=\frac{-\alpha }{2\alpha ({\alpha }^2+1)}=\frac{-1}{2({\alpha }^2+1)}$$$$b=\frac{\alpha }{(-2\alpha )(1+{\alpha }^2)}$$$${lim}_{x\to +\mathrm{\infty }}xF\left(x\right)=0=a+b+c\Rightarrow c=\frac{1}{2({\alpha }^2+1)}+\frac{1}{2(1+{\alpha }^2)}=\frac{1}{1+{\alpha }^2}$$$$F\left(0\right)=0=-\frac{a}{\alpha }+\frac{b}{\alpha }+d\Rightarrow 0=-a+b+\alpha d=\frac{1}{2({\alpha }^2+1)}-\frac{1}{2(1+{\alpha }^2)}+\alpha d\Rightarrow d=0\Rightarrow$$$$F\left(x\right)=\frac{-1}{2(1+{\alpha }^2)(x-\alpha )}-\frac{1}{2(1+{\alpha }^2)(x+\alpha )}+\frac{1}{1+{\alpha }^2}\frac{x}{1+x^2}\Rightarrow$$$$\int F\left(x\right)dx=-\frac{1}{2(1+{\alpha }^2)}ln\mid x^2-{\alpha }^2\mid +\frac{1}{2(1+{\alpha }^2)}ln(x^2+1)+c\Rightarrow$$$$f^{{}^{\prime }}\left(\alpha \right)=-\frac{1}{2(1+{\alpha }^2)}ln\mid {\alpha }^2{u}^2-{\alpha }^2\mid +\frac{1}{2(1+{\alpha }^2)}ln({\alpha }^2{u}^2+1)+c\Rightarrow$$$$f\left(\alpha \right)=\frac{1}{2}{\int }_{.}^{\alpha }\frac{ln\mid t^2{u}^2-t^2\mid }{1+t^2}dt+\frac{1}{2}\int \frac{ln(t^2{u}^2+1)}{1+t^2}dt+c\alpha +\lambda ...becontinued...$$

Commented by maxmathsup by imad last updated on 26/Nov/18

$$letfindIatformofseriewehaveI=\int \frac{t}{cost}dt$$$$I=\int \frac{t}{\frac{e^{it}+e^{-it}}{2}}dt=\int \frac{2t}{e^{it}+e^{-it}}dt=\int \frac{2t{e}^{-it}}{1+e^{-2it}}dt$$$$=2\int t{e}^{-it}\left(\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n{e}^{-2int}\right)dt=2\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n\int t{e}^{-(2n+1)it}dt$$$$=2\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n{A}_{n}byparts{A}_n=-\frac{1}{(2n+1)i}t{e}^{-(2n+1)it}-\int -\frac{1}{(2n+1)i}{e}^{-(2n+1)it}dt$$$$=\frac{it}{2n+1}{e}^{-(2n+1)it}-\frac{i}{2n+1}(-\frac{1}{(2n+1)i})e^{-(2n+1)it}$$$$=\frac{it}{2n+1}{e}^{-(2n+1)it}+\frac{1}{{(2n+1)}^2}{e}^{-(2n+1)it}\Rightarrow$$$$\sum _{n=0}^{\mathrm{\infty }}{A}_n=it\sum _{n=0}^{\mathrm{\infty }}\frac{e^{-(2n+1)it}}{2n+1}+\sum _{n=0}^{\mathrm{\infty }}\frac{e^{-(2n+1)it}}{{(2n+1)}^2}....becontinued...$$

Answered by Abdulhafeez Abu qatada last updated on 21/Nov/18

Terms of Service

Privacy Policy

Contact: info@tinkutara.com