let f(x) =∫_(1/2) ^1 (dt/(2+ch(xt))) 1) find a explicit form of f(x) 2) calculate g(x)=∫_(1/2) ^1 ((tsh(xt))/((2+ch(xt))^2 ))dt 3) find the value of ∫_(1/2) ^1 (dt/(2+ch(3t))) and ∫_(1/2) ^1 ((tsh(2t))/((2+ch(2t))^2 ))dt 4) let u_n =∫_(1/2) ^1 (dt/(2+ch(nt))) study the convergence of Σu_n and Σ(u


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 48261 by Abdo msup. last updated on 21/Nov/18

$l e t f (x) = \int_{\frac{1}{2}}^{1} \frac{d t}{2 + c h (x t)}$ $1) f i n d a e x p l i c i t f o r m o f f (x)$ $2) c a l c u l a t e g (x) = \int_{\frac{1}{2}}^{1} \frac{t s h (x t)}{{(2 + c h (x t))}^{2}} d t$ $3) f i n d t h e v a l u e o f \int_{\frac{1}{2}}^{1} \frac{d t}{2 + c h (3 t)} a n d \int_{\frac{1}{2}}^{1} \frac{t s h (2 t)}{{(2 + c h (2 t))}^{2}} d t$ $4) l e t u_{n} = \int_{\frac{1}{2}}^{1} \frac{d t}{2 + c h (n t)} s t u d y t h e c o n v e r g e n c e o f Σ u_{n}$ $a n d Σ \frac{u_{n}}{n} .$
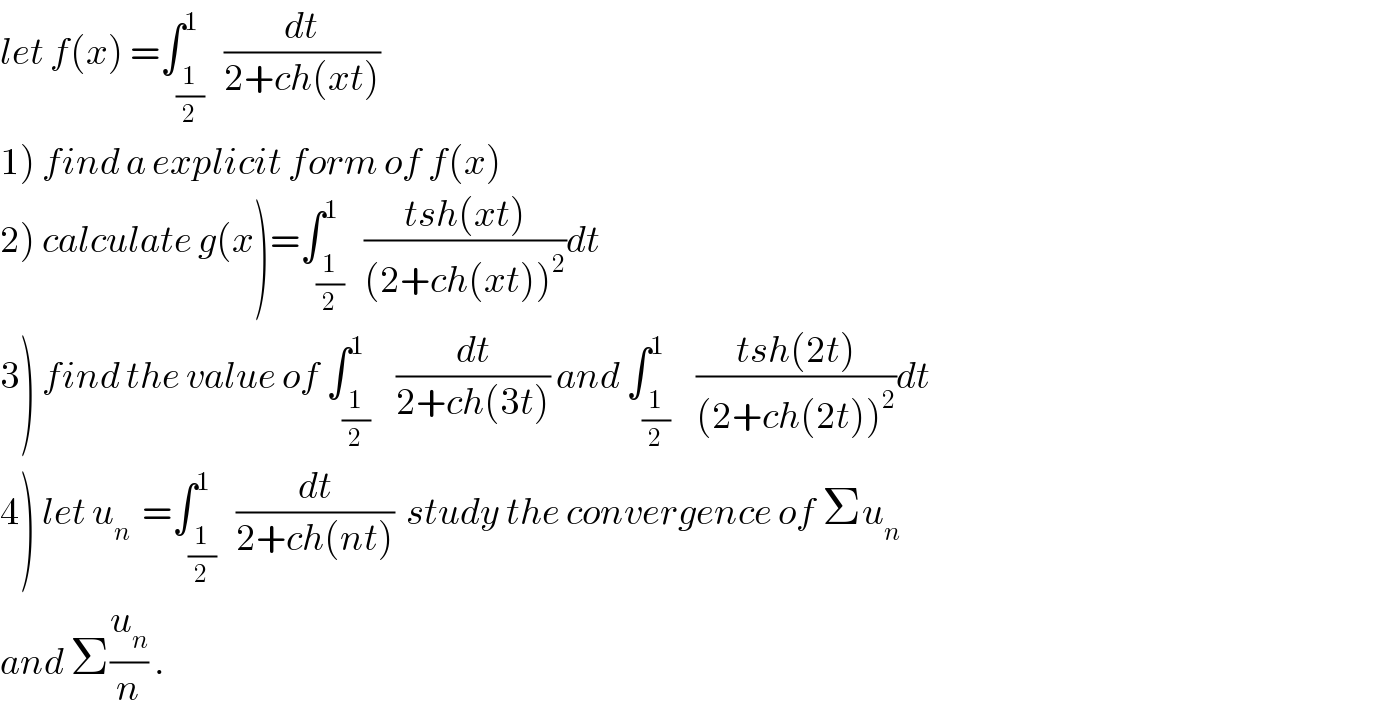
Commented by maxmathsup by imad last updated on 22/Nov/18
$1) we have for x ≠0f(x)=∫_(1/2) ^1 (dt/(2+ch(xt))) =_(xt=u) ∫_(x/2) ^x (du/(x(2+ch(u))) =(1/x) ∫_(x/2) ^x (du/(2+((e^u +e^(−u) )/2))) =(2/x) ∫_(x/2) ^x (du/(4 +e^u +e^(−u) )) =_(e^u =α) (2/x) ∫_e^(x/2) ^e^x (dα/(α(4+α +α^(−1) ))) =(2/x) ∫_e^(x/2) ^e^x (dα/(α^2 +4α +1)) =(2/x) ∫_e^(x/2) ^e^x (dα/((α+2)^2 −3)) =(2/x) ∫_e^(x/2) ^e^x (dα/((α−1)(α+5))) =(1/(3x)) ∫_e^(x/2) ^e^x {(1/(α−1)) −(1/(α+5))}dα = (1/(3x))[ln∣((α−1)/(α+5))∣]_e^(x/2) ^e^x =(1/(3x)){ln∣((e^x −1)/(e^x +5))∣−ln∣((e^(x/2) −1)/(e^(x/2) +5))∣}$
$1) w e h a v e f o r x \neq 0 f (x) = \int_{\frac{1}{2}}^{1} \frac{d t}{2 + c h (x t)} =_{x t = u} \int_{\frac{x}{2}}^{x} \frac{d u}{x (2 + c h (u)}$ $= \frac{1}{x} \int_{\frac{x}{2}}^{x} \frac{d u}{2 + \frac{e^{u} + e^{- u}}{2}} = \frac{2}{x} \int_{\frac{x}{2}}^{x} \frac{d u}{4 + e^{u} + e^{- u}} =_{e^{u} = α} \frac{2}{x} \int_{e^{\frac{x}{2}}}^{e^{x}} \frac{d α}{α (4 + α + α^{- 1})}$ $= \frac{2}{x} \int_{e^{\frac{x}{2}}}^{e^{x}} \frac{d α}{α^{2} + 4 α + 1} = \frac{2}{x} \int_{e^{\frac{x}{2}}}^{e^{x}} \frac{d α}{{(α + 2)}^{2} - 3} = \frac{2}{x} \int_{e^{\frac{x}{2}}}^{e^{x}} \frac{d α}{(α - 1) (α + 5)}$ $= \frac{1}{3 x} \int_{e^{\frac{x}{2}}}^{e^{x}} {\frac{1}{α - 1} - \frac{1}{α + 5}} d α = \frac{1}{3 x} {[l n ∣ \frac{α - 1}{α + 5} ∣]}_{e^{\frac{x}{2}}}^{e^{x}}$ $= \frac{1}{3 x} {l n ∣ \frac{e^{x} - 1}{e^{x} + 5} ∣ - l n ∣ \frac{e^{\frac{x}{2}} - 1}{e^{\frac{x}{2}} + 5} ∣}$
Commented by maxmathsup by imad last updated on 22/Nov/18
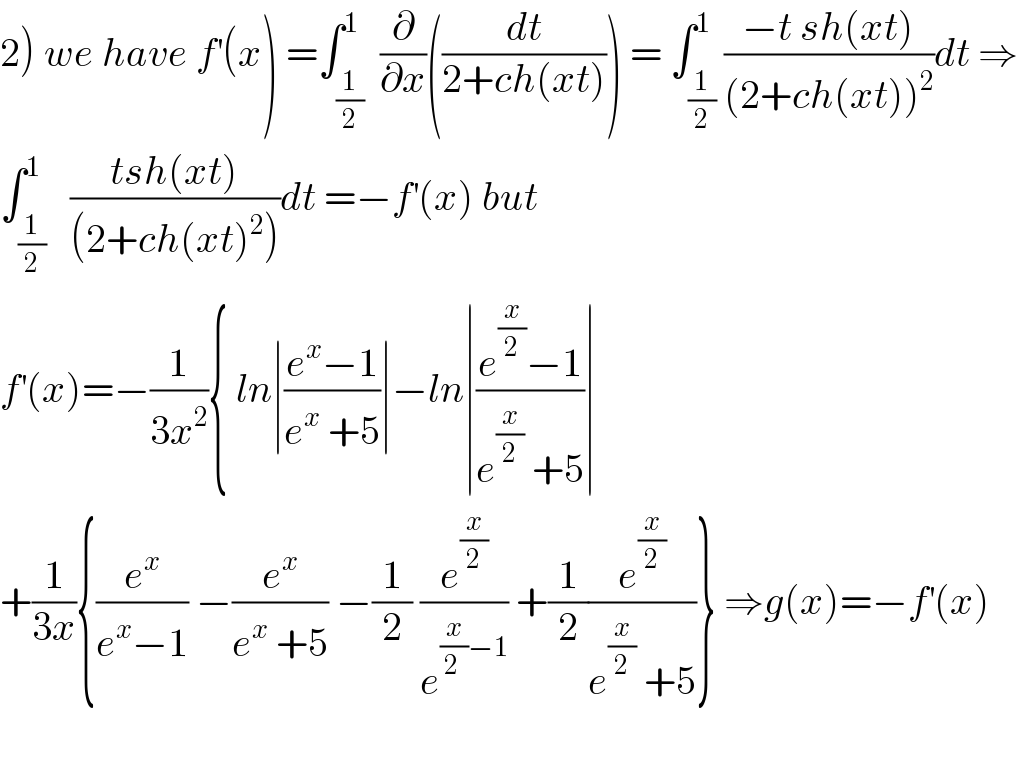
$2) we have f^′ (x) =∫_(1/2) ^1 (∂/∂x)((dt/(2+ch(xt)))) = ∫_(1/2) ^1 ((−t sh(xt))/((2+ch(xt))^2 ))dt ⇒ ∫_(1/2) ^1 ((tsh(xt))/((2+ch(xt)^2 )))dt =−f^′ (x) but f^′ (x)=−(1/(3x^2 )){ ln∣((e^x −1)/(e^x +5))∣−ln∣((e^(x/2) −1)/(e^(x/2) +5))∣ +(1/(3x)){(e^x /(e^x −1)) −(e^x /(e^x +5)) −(1/2) (e^(x/2) /e^((x/(2 ))−1) ) +(1/2)(e^(x/2) /(e^(x/2) +5))} ⇒g(x)=−f^′ (x)$
$2) w e h a v e f^{^{'}} (x) = \int_{\frac{1}{2}}^{1} \frac{\partial}{\partial x} (\frac{d t}{2 + c h (x t)}) = \int_{\frac{1}{2}}^{1} \frac{- t s h (x t)}{{(2 + c h (x t))}^{2}} d t \Rightarrow$ $\int_{\frac{1}{2}}^{1} \frac{t s h (x t)}{(2 + c h {(x t)}^{2})} d t = - f^{^{'}} (x) b u t$ $f^{^{'}} (x) = - \frac{1}{3 x^{2}} {l n ∣ \frac{e^{x} - 1}{e^{x} + 5} ∣ - l n ∣ \frac{e^{\frac{x}{2}} - 1}{e^{\frac{x}{2}} + 5} ∣$ $+ \frac{1}{3 x} {\frac{e^{x}}{e^{x} - 1} - \frac{e^{x}}{e^{x} + 5} - \frac{1}{2} \frac{e^{\frac{x}{2}}}{e^{\frac{x}{2} - 1}} + \frac{1}{2} \frac{e^{\frac{x}{2}}}{e^{\frac{x}{2}} + 5}} \Rightarrow g (x) = - f^{^{'}} (x)$
Commented by maxmathsup by imad last updated on 22/Nov/18
$3) ∫_(1/2) ^1 (dt/(2+ch(3t))) =f(3)=(1/9){ln∣((e^3 −1)/(e^3 +5))∣−ln∣((e^(3/2) −1)/(e^(3/2) +5))∣$
$3) \int_{\frac{1}{2}}^{1} \frac{d t}{2 + c h (3 t)} = f (3) = \frac{1}{9} {l n ∣ \frac{e^{3} - 1}{e^{3} + 5} ∣ - l n ∣ \frac{e^{\frac{3}{2}} - 1}{e^{\frac{3}{2}} + 5} ∣$
Commented by maxmathsup by imad last updated on 22/Nov/18
$∫_(1/2) ^1 ((tsh(2t))/((2+ch(2t))^2 ))dt =g(2) =−f^′ (2) =(1/(12)){ln∣((e^2 −1)/(e^2 +5))∣−ln∣((e−1)/(e+5))∣} +(1/6){ (e^2 /(e^2 −1)) −(e^2 /(e^2 +5)) −(1/2) (e/(e−1)) +(1/2) (e/(e+5))}$
$\int_{\frac{1}{2}}^{1} \frac{t s h (2 t)}{{(2 + c h (2 t))}^{2}} d t = g (2) = - f^{^{'}} (2) = \frac{1}{12} {l n ∣ \frac{e^{2} - 1}{e^{2} + 5} ∣ - l n ∣ \frac{e - 1}{e + 5} ∣}$ $+ \frac{1}{6} {\frac{e^{2}}{e^{2} - 1} - \frac{e^{2}}{e^{2} + 5} - \frac{1}{2} \frac{e}{e - 1} + \frac{1}{2} \frac{e}{e + 5}}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum