
Question and Answers Forum
Question Number 48272 by gunawan last updated on 21/Nov/18
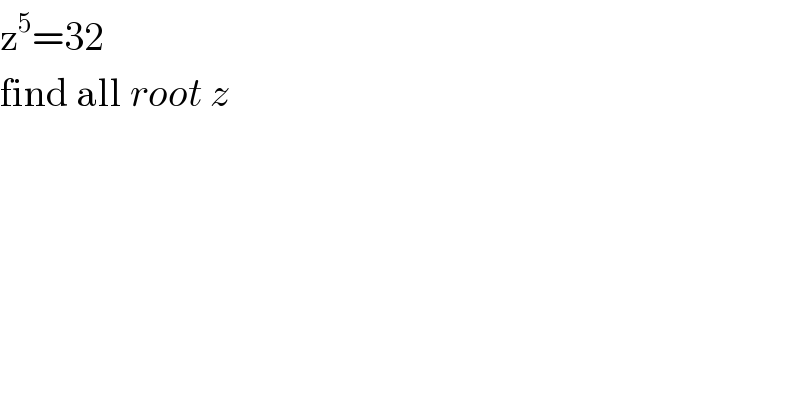
Commented by maxmathsup by imad last updated on 21/Nov/18
![let z=r e^(iθ) so z^5 =32 ⇔r^5 e^(5iθ) =2^5 e^(i2kπ) ⇔r=2 and 5θ =2kπ ⇒ θ_k =((2kπ)/5) so the roots are z_k =2 e^(i((2kπ)/5)) and k∈[[0,4]] z_0 =2 ,z_1 =2 e^(i((2π)/5)) ,z_2 =2 e^(i((4π)/5)) , z_3 =2 e^(i((6π)/5)) , z_(4 ) =2 e^(i((8π)/5)) . z_1 =2(cos(((2π)/5))+isin(((2π)/5))) but cos(((2π)/5))=2cos^2 ((π/5))−1 =2(((1+(√5))/4))^2 −1 =2((6+2(√5))/(16)) −1 =((12+4(√5)−16)/(16)) =((4(√5)−4)/(16)) =(((√5)−1)/4) sin(((2π)/5))=(√(1−((((√5)−1)/4))^2 ))=(√(1−((6−2(√5))/(16))))=(√((10+2(√5))/(16)))=((√(10+2(√5)))/4) ⇒ z_1 =(((√5)−1)/2) +i((√(10+2(√5)))/2) z_2 =2 e^(i(π−(π/5))) =−2 e^(−i(π/5)) =−2(cos((π/5))−isin((π/5)))but cos((π/5))=((1+(√5))/4) sin((π/5))=(√(1−(((1+(√5))/4))^2 ))=(√(1−((6+2(√5))/(16))))=(√((10−2(√5))/(16)))=((√(10−2(√5)))/4) ⇒ z_2 =−((1+(√5))/2) +i((√(10−2(√5)))/2) z_3 =2 e^(iπ) e^(i(π/5)) =−2(cos((π/5))+isin((π/5))) =−((1+(√5))/2) −i((√(10−2(√5)))/2) z_4 =2 e^(i(2π−((2π)/5))) =2 e^(−i((2π)/5)) =2(cos(((2π)/5))−isin(((2π)/5))) =(((√5)−1)/2) −i((√(10+(√5)))/2)](Q48274.png)
| ||
Question and Answers Forum | ||
Question Number 48272 by gunawan last updated on 21/Nov/18 | ||
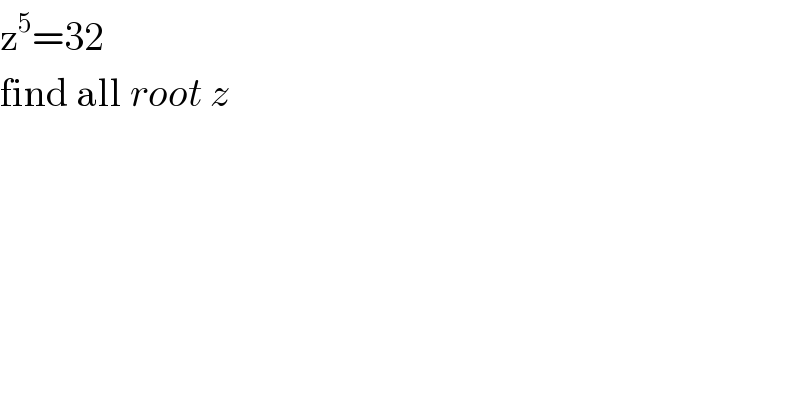 | ||
Commented by maxmathsup by imad last updated on 21/Nov/18 | ||
![let z=r e^(iθ) so z^5 =32 ⇔r^5 e^(5iθ) =2^5 e^(i2kπ) ⇔r=2 and 5θ =2kπ ⇒ θ_k =((2kπ)/5) so the roots are z_k =2 e^(i((2kπ)/5)) and k∈[[0,4]] z_0 =2 ,z_1 =2 e^(i((2π)/5)) ,z_2 =2 e^(i((4π)/5)) , z_3 =2 e^(i((6π)/5)) , z_(4 ) =2 e^(i((8π)/5)) . z_1 =2(cos(((2π)/5))+isin(((2π)/5))) but cos(((2π)/5))=2cos^2 ((π/5))−1 =2(((1+(√5))/4))^2 −1 =2((6+2(√5))/(16)) −1 =((12+4(√5)−16)/(16)) =((4(√5)−4)/(16)) =(((√5)−1)/4) sin(((2π)/5))=(√(1−((((√5)−1)/4))^2 ))=(√(1−((6−2(√5))/(16))))=(√((10+2(√5))/(16)))=((√(10+2(√5)))/4) ⇒ z_1 =(((√5)−1)/2) +i((√(10+2(√5)))/2) z_2 =2 e^(i(π−(π/5))) =−2 e^(−i(π/5)) =−2(cos((π/5))−isin((π/5)))but cos((π/5))=((1+(√5))/4) sin((π/5))=(√(1−(((1+(√5))/4))^2 ))=(√(1−((6+2(√5))/(16))))=(√((10−2(√5))/(16)))=((√(10−2(√5)))/4) ⇒ z_2 =−((1+(√5))/2) +i((√(10−2(√5)))/2) z_3 =2 e^(iπ) e^(i(π/5)) =−2(cos((π/5))+isin((π/5))) =−((1+(√5))/2) −i((√(10−2(√5)))/2) z_4 =2 e^(i(2π−((2π)/5))) =2 e^(−i((2π)/5)) =2(cos(((2π)/5))−isin(((2π)/5))) =(((√5)−1)/2) −i((√(10+(√5)))/2)](Q48274.png) | ||