Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 48294 by behi83417@gmail.com last updated on 21/Nov/18

Commented by MJS last updated on 22/Nov/18

x^6 +x^5 +x^4 −10x^3 +x^2 +x+1=0 x=tan (t/2) after some transforming work we get ((3sin^3 t +sin^2 t −sin t −2)/((1+cos t)^3 ))=0 sin t =y 3y^3 +y^2 −y−2=0 y^3 +(1/3)y^2 −(1/3)y−(2/3)=0 y=z−(1/9) z^3 −((10)/(27))z−((457)/(729))=0 D=(p^3 /(27))+(q^2 /4)=((281)/(2916))>0 ⇒ 1 real solution z=((−(q/2)+(√((p^3 /(27))+(q^2 /4)))))^(1/3) +((−(q/2)−(√((p^3 /(27))+(q^2 /4)))))^(1/3) z=(1/9)((((457+27(√(281)))/2))^(1/3) +(((457−27(√(281)))/2))^(1/3) ) y=(1/9)((((457+27(√(281)))/2))^(1/3) +(((457−27(√(281)))/2))^(1/3) −1) t=2nπ+arcsin y ∨ t=(2n+1)π−arcsin y ; n∈Z x=tan ((arcsin y)/2) ∨ x=cot ((arcsin y)/2) x=(1/y)±((√(1−y^2 ))/y) ...so we have exact solutions of an unpleasant shape x_1 ≈.608053 x_2 ≈1.64459

$${x}^{\mathrm{6}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\mathrm{tan}\:\frac{{t}}{\mathrm{2}} \\ $$$$\mathrm{after}\:\mathrm{some}\:\mathrm{transforming}\:\mathrm{work}\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{3sin}^{\mathrm{3}} \:{t}\:+\mathrm{sin}^{\mathrm{2}} \:{t}\:−\mathrm{sin}\:{t}\:−\mathrm{2}}{\left(\mathrm{1}+\mathrm{cos}\:{t}\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$$\mathrm{sin}\:{t}\:={y} \\ $$$$\mathrm{3}{y}^{\mathrm{3}} +{y}^{\mathrm{2}} −{y}−\mathrm{2}=\mathrm{0} \\ $$$${y}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}{y}−\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{0} \\ $$$${y}={z}−\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{10}}{\mathrm{27}}{z}−\frac{\mathrm{457}}{\mathrm{729}}=\mathrm{0} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{281}}{\mathrm{2916}}>\mathrm{0}\:\Rightarrow\:\mathrm{1}\:\mathrm{real}\:\mathrm{solution} \\ $$$${z}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}}+\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$$${z}=\frac{\mathrm{1}}{\mathrm{9}}\left(\sqrt[{\mathrm{3}}]{\frac{\mathrm{457}+\mathrm{27}\sqrt{\mathrm{281}}}{\mathrm{2}}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{457}−\mathrm{27}\sqrt{\mathrm{281}}}{\mathrm{2}}}\right) \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{9}}\left(\sqrt[{\mathrm{3}}]{\frac{\mathrm{457}+\mathrm{27}\sqrt{\mathrm{281}}}{\mathrm{2}}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{457}−\mathrm{27}\sqrt{\mathrm{281}}}{\mathrm{2}}}−\mathrm{1}\right) \\ $$$${t}=\mathrm{2}{n}\pi+\mathrm{arcsin}\:{y}\:\vee\:{t}=\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\mathrm{arcsin}\:{y}\:;\:{n}\in\mathbb{Z} \\ $$$${x}=\mathrm{tan}\:\frac{\mathrm{arcsin}\:{y}}{\mathrm{2}}\:\vee\:{x}=\mathrm{cot}\:\frac{\mathrm{arcsin}\:{y}}{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{1}}{{y}}\pm\frac{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}{{y}} \\ $$$$...\mathrm{so}\:\mathrm{we}\:\mathrm{have}\:\mathrm{exact}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{an}\:\mathrm{unpleasant}\:\mathrm{shape} \\ $$$${x}_{\mathrm{1}} \approx.\mathrm{608053} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{1}.\mathrm{64459} \\ $$

Commented by MJS last updated on 22/Nov/18

(x−(1/y)+((√(1−y^2 ))/y))(x−(1/y)−((√(1−y^2 ))/y))=x^2 −(2/y)+1 ((x^6 +x^5 +x^4 −10x^3 +x^2 +x+1)/(x^2 −(2/y)+1))= =x^4 +(1+(2/y))x^3 +((2/y)+(4/y^2 ))x^2 −(11+(2/y)−(4/y^2 )−(8/y^3 ))x+(1−((24)/y)−(8/y^2 )+(8/y^3 )+((16)/y^4 ))+F F=((4((y^2 −4)x+2y))/(y^5 (x^2 −(2/y)+1)))(3y^2 +y^2 −y−2) and since F=0 we get the same solution as above. not sure which method is more comfortable

$$\left({x}−\frac{\mathrm{1}}{{y}}+\frac{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}{{y}}\right)\left({x}−\frac{\mathrm{1}}{{y}}−\frac{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}{{y}}\right)={x}^{\mathrm{2}} −\frac{\mathrm{2}}{{y}}+\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{6}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\frac{\mathrm{2}}{{y}}+\mathrm{1}}= \\ $$$$={x}^{\mathrm{4}} +\left(\mathrm{1}+\frac{\mathrm{2}}{{y}}\right){x}^{\mathrm{3}} +\left(\frac{\mathrm{2}}{{y}}+\frac{\mathrm{4}}{{y}^{\mathrm{2}} }\right){x}^{\mathrm{2}} −\left(\mathrm{11}+\frac{\mathrm{2}}{{y}}−\frac{\mathrm{4}}{{y}^{\mathrm{2}} }−\frac{\mathrm{8}}{{y}^{\mathrm{3}} }\right){x}+\left(\mathrm{1}−\frac{\mathrm{24}}{{y}}−\frac{\mathrm{8}}{{y}^{\mathrm{2}} }+\frac{\mathrm{8}}{{y}^{\mathrm{3}} }+\frac{\mathrm{16}}{{y}^{\mathrm{4}} }\right)+{F} \\ $$$${F}=\frac{\mathrm{4}\left(\left({y}^{\mathrm{2}} −\mathrm{4}\right){x}+\mathrm{2}{y}\right)}{{y}^{\mathrm{5}} \left({x}^{\mathrm{2}} −\frac{\mathrm{2}}{{y}}+\mathrm{1}\right)}\left(\mathrm{3}{y}^{\mathrm{2}} +{y}^{\mathrm{2}} −{y}−\mathrm{2}\right) \\ $$$$\mathrm{and}\:\mathrm{since}\:{F}=\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{solution}\:\mathrm{as} \\ $$$$\mathrm{above}.\:\mathrm{not}\:\mathrm{sure}\:\mathrm{which}\:\mathrm{method}\:\mathrm{is}\:\mathrm{more}\:\mathrm{comfortable} \\ $$

Commented by behi83417@gmail.com last updated on 22/Nov/18

thank you so much dear MJS,Ajfour and sir tanmay.

$${thank}\:{you}\:{so}\:{much}\:{dear}\:{MJS},{Ajfour} \\ $$$${and}\:{sir}\:{tanmay}. \\ $$

Answered by ajfour last updated on 22/Nov/18

let (1/x) = t ⇒ (1+t)((1/t)+t)((1/t^2 )+t)=12 or (t+1)(t^2 +1)(t^3 +1)=12t^3 ⇒ if α is a root, then (1/α) is also a root. ⇒ Π(x−α)(x−(1/α))=0 or Π[x^2 −(α+(1/α))x+1]=0 let α+(1/α) = p , β+(1/β) = q , γ+(1/γ)=r Π(x^2 −px+1)=0 x^6 −(p+q+r)x^5 +(3+pq+qr+rp)x^4 −(p+q+r+pqr)x^3 +(3+pq+qr+rp)x^2 −(p+q+r)x +1 = 0 given eq. (x+1)(x^2 +1)(x^3 +1)=12x^3 ⇒ x^6 +x^5 +x^4 −10x^3 +x^2 +x+1=0 ⇒ p+q+r = −1 pq+qr+rp = −2 pqr = 11 p,q,r are then roots of t^3 +t^2 −2t−11=0 should be t^3 +t^2 −2t−12 = 0 _________________________ BUT HOW ? _________________________ t=p ≈ 2.19479 (only one real root). ⇒ α+(1/α) = p α^2 −pα+1 = 0 some error ...

$${let}\:\:\frac{\mathrm{1}}{{x}}\:=\:{t} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{1}+{t}\right)\left(\frac{\mathrm{1}}{{t}}+{t}\right)\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+{t}\right)=\mathrm{12} \\ $$$${or}\:\:\:\:\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{3}} +\mathrm{1}\right)=\mathrm{12}{t}^{\mathrm{3}} \\ $$$$\Rightarrow\:\:{if}\:\alpha\:{is}\:{a}\:{root},\:{then}\:\frac{\mathrm{1}}{\alpha}\:{is}\:{also} \\ $$$${a}\:{root}. \\ $$$$\Rightarrow\:\:\:\Pi\left({x}−\alpha\right)\left({x}−\frac{\mathrm{1}}{\alpha}\right)=\mathrm{0} \\ $$$${or}\:\:\:\:\:\Pi\left[{x}^{\mathrm{2}} −\left(\alpha+\frac{\mathrm{1}}{\alpha}\right){x}+\mathrm{1}\right]=\mathrm{0} \\ $$$${let}\:\alpha+\frac{\mathrm{1}}{\alpha}\:=\:{p}\:,\:\beta+\frac{\mathrm{1}}{\beta}\:=\:{q}\:,\:\gamma+\frac{\mathrm{1}}{\gamma}={r} \\ $$$$\:\:\:\:\:\:\:\:\Pi\left({x}^{\mathrm{2}} −{px}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{6}} −\left({p}+{q}+{r}\right){x}^{\mathrm{5}} +\left(\mathrm{3}+{pq}+{qr}+{rp}\right){x}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:−\left({p}+{q}+{r}+{pqr}\right){x}^{\mathrm{3}} \\ $$$$+\left(\mathrm{3}+{pq}+{qr}+{rp}\right){x}^{\mathrm{2}} −\left({p}+{q}+{r}\right){x} \\ $$$$\:\:\:\:\:\:\:+\mathrm{1}\:=\:\mathrm{0} \\ $$$${given}\:{eq}.\:\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{3}} +\mathrm{1}\right)=\mathrm{12}{x}^{\mathrm{3}} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{6}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:{p}+{q}+{r}\:=\:−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{pq}+{qr}+{rp}\:=\:−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:{pqr}\:=\:\mathrm{11} \\ $$$${p},{q},{r}\:{are}\:{then}\:{roots}\:{of} \\ $$$$\:\:\:\:\:\:\:\:\:{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{11}=\mathrm{0} \\ $$$${should}\:{be}\:\:{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{12}\:=\:\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:\:\:\mathbb{BUT}\:\:\mathbb{HOW}\:? \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:{t}={p}\:\approx\:\mathrm{2}.\mathrm{19479}\:\:\:\left({only}\:{one}\:{real}\:{root}\right). \\ $$$$\Rightarrow\:\:\:\alpha+\frac{\mathrm{1}}{\alpha}\:=\:{p} \\ $$$$\:\:\:\:\alpha^{\mathrm{2}} −{p}\alpha+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\: \\ $$$$\:\:{some}\:{error}\:\:... \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 22/Nov/18

x^6 +x^5 +x^4 −10x^3 +x^2 +x+1=0 x^3 +x^2 +x−10+(1/x)+(1/x^2 )+(1/x^3 )=0 (x^3 +(1/x^3 ))+(x^2 +(1/x^2 ))+(x+(1/x))−10=0 t=x+(1/x) t^3 −3t+t^2 −2+t−10=0 t^3 +t^2 −2t−12=0 f(t)=t^3 +t^2 −2t−12 f(0)<0 f(1)<0 f(2)<0 but f(3)>0 so one root of eqn t^3 +t^2 −2t−12=0 lies in between 2 and 3 now calculating value of f(2.2) and f(2.3) using calculus f(t)=t^3 +t^2 −2t−12 f(2)=−4 (df/dt)=((△f)/(△t))=3t^2 +2t−2 so (df/dt)=14 at t=2 ((△f)/(△t))=(df/dt) △f=(df/dt)△t=14×0.2=2.8 so f(2.2)=−4+2.8=−1.2 f(2.3)=−4+4.2=0.2 f(2.2)<0 but f(2.3)>0 so one root of eqn t^3 +t^2 −2t−12=0 lies between 2.2 and 2.3 so let 2.3 >α>2.2 is solution of t^3 +t^2 −2t−12=0 x+(1/x)=α x^2 −αx+1=0 x=((α±(√(α^2 −4)))/2) we can find α using approxmiatation ....

$${x}^{\mathrm{6}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}−\mathrm{10}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)+\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{10}=\mathrm{0} \\ $$$${t}={x}+\frac{\mathrm{1}}{{x}} \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{t}+{t}^{\mathrm{2}} −\mathrm{2}+{t}−\mathrm{10}=\mathrm{0} \\ $$$${t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{12}=\mathrm{0} \\ $$$${f}\left({t}\right)={t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{12} \\ $$$${f}\left(\mathrm{0}\right)<\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)<\mathrm{0} \\ $$$${f}\left(\mathrm{2}\right)<\mathrm{0}\:\:{but}\:{f}\left(\mathrm{3}\right)>\mathrm{0} \\ $$$${so}\:{one}\:{root}\:{of}\:{eqn}\:{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{12}=\mathrm{0} \\ $$$${lies}\:{in}\:{between}\:\mathrm{2}\:{and}\:\mathrm{3} \\ $$$${now}\:{calculating}\:{value}\:{of}\:{f}\left(\mathrm{2}.\mathrm{2}\right)\:{and}\:{f}\left(\mathrm{2}.\mathrm{3}\right)\:{using} \\ $$$${calculus} \\ $$$${f}\left({t}\right)={t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{12} \\ $$$${f}\left(\mathrm{2}\right)=−\mathrm{4} \\ $$$$\frac{{df}}{{dt}}=\frac{\bigtriangleup{f}}{\bigtriangleup{t}}=\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{2} \\ $$$${so}\:\frac{{df}}{{dt}}=\mathrm{14}\:\:{at}\:{t}=\mathrm{2} \\ $$$$\frac{\bigtriangleup{f}}{\bigtriangleup{t}}=\frac{{df}}{{dt}} \\ $$$$\bigtriangleup{f}=\frac{{df}}{{dt}}\bigtriangleup{t}=\mathrm{14}×\mathrm{0}.\mathrm{2}=\mathrm{2}.\mathrm{8} \\ $$$${so}\:{f}\left(\mathrm{2}.\mathrm{2}\right)=−\mathrm{4}+\mathrm{2}.\mathrm{8}=−\mathrm{1}.\mathrm{2} \\ $$$${f}\left(\mathrm{2}.\mathrm{3}\right)=−\mathrm{4}+\mathrm{4}.\mathrm{2}=\mathrm{0}.\mathrm{2} \\ $$$${f}\left(\mathrm{2}.\mathrm{2}\right)<\mathrm{0}\:\:\:{but}\:{f}\left(\mathrm{2}.\mathrm{3}\right)>\mathrm{0} \\ $$$${so}\:{one}\:{root}\:{of}\:{eqn}\:{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{12}=\mathrm{0} \\ $$$${lies}\:{between}\:\mathrm{2}.\mathrm{2}\:{and}\:\mathrm{2}.\mathrm{3} \\ $$$${so}\:{let}\:\mathrm{2}.\mathrm{3}\:>\alpha>\mathrm{2}.\mathrm{2}\:{is}\:{solution}\:{of}\:{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{12}=\mathrm{0} \\ $$$$ \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\alpha \\ $$$${x}^{\mathrm{2}} −\alpha{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\alpha\pm\sqrt{\alpha^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$${we}\:{can}\:{find}\:\alpha\:{using}\:{approxmiatation}\:.... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by behi83417@gmail.com last updated on 22/Nov/18

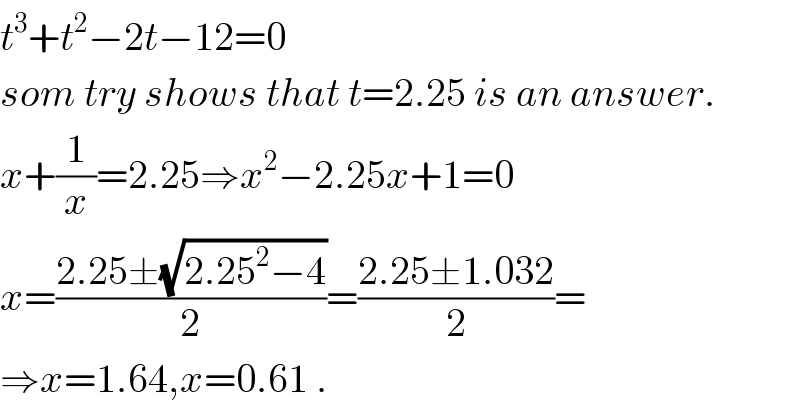
t^3 +t^2 −2t−12=0 som try shows that t=2.25 is an answer. x+(1/x)=2.25⇒x^2 −2.25x+1=0 x=((2.25±(√(2.25^2 −4)))/2)=((2.25±1.032)/2)= ⇒x=1.64,x=0.61 .

$${t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{12}=\mathrm{0} \\ $$$${som}\:{try}\:{shows}\:{that}\:{t}=\mathrm{2}.\mathrm{25}\:{is}\:{an}\:{answer}. \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{2}.\mathrm{25}\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}.\mathrm{25}{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2}.\mathrm{25}\pm\sqrt{\mathrm{2}.\mathrm{25}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{2}.\mathrm{25}\pm\mathrm{1}.\mathrm{032}}{\mathrm{2}}= \\ $$$$\Rightarrow{x}=\mathrm{1}.\mathrm{64},{x}=\mathrm{0}.\mathrm{61}\:. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 22/Nov/18

thank you sir..

$${thank}\:{you}\:{sir}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com